Монитор фильтра частиц ошибка
Обновлено: 23.04.2024
Я понял основной принцип фильтра частиц и попытался реализовать его. Тем не менее, я зациклился на части пересэмплирования.
Теоретически, это довольно просто: из старого (и взвешенного) набора частиц нарисуйте новый набор частиц с заменой. При этом отдавайте предпочтение тем частицам, которые имеют большой вес. Частицы с большим весом вытягиваются чаще, а частицы с низким весом - реже. Возможно только один раз или не совсем. После повторной выборки всем весам присваивается одинаковый вес.
Моя первая идея о том, как реализовать это, была, по сути, такой:
- Нормализовать вес
- Умножьте каждый вес на общее количество частиц
- Округлите эти весы до ближайшего целого (например, с помощью int() в Python)
Теперь я должен знать, как часто нужно рисовать каждую частицу, но из-за ошибок округления у меня получается меньше частиц, чем до этапа повторной выборки.
Вопрос: Как «заполнить» отсутствующие частицы, чтобы получить то же количество частиц, что и до шага повторной выборки? Или, если я совершенно не в курсе, как мне правильно сделать повторную выборку?
Проблема, с которой вы сталкиваетесь, часто называется пробным обнищанием. Мы можем видеть, почему ваш подход страдает от этого на довольно простом примере. Допустим, у вас есть 3 частицы, и их нормализованные веса равны 0,1, 0,1, 0,8. Затем умножение каждого веса на 3 дает 0,3, 0,3 и 2,4. Затем округление дает 0, 0, 2. Это означает, что вы не выберете первые две частицы, а последняя будет выбрана дважды. Теперь вы до двух частиц. Я подозреваю, что это то, что вы видели, когда говорите «из-за ошибок округления у меня в конечном итоге будет меньше частиц».
Альтернативный метод выбора будет следующим.
- Нормализовать вес.
- Рассчитать массив совокупной суммы весов.
- Произвольно сгенерируйте число и определите, к какому диапазону в этом массиве совокупного веса принадлежит данное число.
- Индекс этого диапазона будет соответствовать частице, которая должна быть создана.
- Повторяйте, пока не получите желаемое количество образцов.
Итак, используя приведенный выше пример, мы начнем с нормализованных весов. Затем мы вычислим массив [0,1, 0,2, 1]. Оттуда мы вычисляем 3 случайных числа, скажем, 0,15, 0,38 и 0,54. Это заставило бы нас выбрать вторую частицу один раз, а третью - дважды. Дело в том, что это дает мелким частицам возможность размножаться.
Следует отметить, что хотя этот метод будет бороться с обнищанием, он может привести к неоптимальным решениям. Например, может случиться так, что ни одна из частиц в действительности не будет соответствовать вашему заданному местоположению (при условии, что вы используете это для локализации). Вес только говорит вам, какие частицы соответствуют лучше всего, а не качество соответствует. Таким образом, когда вы берете дополнительные показания и повторяете процесс, вы можете обнаружить, что все ваши частицы группируются в одном месте, которое не является правильным. Обычно это потому, что не было хороших частиц для начала.
Спасибо за проницательный ответ! Метод выбора, который вы предложили, кажется знакомым. Если я правильно помню, это был распространенный способ решения проблемы обнищания выборки. Я видел это раньше, но так и не понял причину этой процедуры. Теперь я знаю лучше! Я думаю, что ваша интерпретация обнищания выборки может быть немного вводящей в заблуждение. Тот факт, что на плакате теряются частицы, вызван неподходящим методом повторной выборки. Обнищание частиц - это когда ваше апостериорное распределение больше не адекватно представлено частицами.Как я полагаю, вы сами выяснили, что метод повторной выборки, который вы предлагаете, немного ошибочен, так как он не должен изменять количество частиц (если вы этого не хотите). Принцип заключается в том, что вес представляет относительную вероятность по отношению к другим частицам. На этапе повторной выборки вы выбираете из набора частиц так, чтобы для каждой частицы нормализованный вес, умноженный на количество частиц, представлял количество раз, которое частица была нарисована в среднем. В этом ваша идея верна. Только используя округление вместо выборки, вы всегда будете удалять частицы, для которых ожидаемое значение меньше половины.
Существует несколько способов правильно выполнить повторную выборку. Есть хорошая статья под названием « Алгоритмы передискретизации для фильтров частиц» , в которой сравниваются различные методы. Просто чтобы дать краткий обзор:
Полиномиальная повторная выборка: представьте полоску бумаги, где каждая частица имеет сечение, длина которого пропорциональна ее весу. Случайно выберите место на полосе N раз и выберите частицу, связанную с разрезом.
Остаточная повторная выборка: этот подход пытается уменьшить дисперсию выборки, сначала выделяя каждой частице их целое минимальное значение ожидаемого значения, а оставшуюся часть оставляют для многочленной повторной выборки. Например, частица с ожидаемым значением 2,5 будет иметь 2 копии в наборе с измененной выборкой и еще одну с ожидаемым значением 0,5.
Систематическая повторная выборка: возьмите линейку с правильными разнесенными отметками, так чтобы отметки N имели ту же длину, что и ваша полоска бумаги. Случайно поместите линейку рядом с вашей полосой. Возьмите частицы на отметках.
Стратифицированная повторная выборка: такая же, как и систематическая повторная выборка, за исключением того, что метки на линейке размещаются неравномерно, а добавляются как N случайных выборочных процессов из интервала 0..1 / N
Итак, чтобы ответить на ваш вопрос: то, что вы реализовали, может быть расширено до формы остаточной выборки. Вы заполняете недостающие слоты путем выборки, основываясь на многовековом распределении напоминаний.
Фильтрализация урок частиц фильтра частицы: поскольку вывод к применению (2)
Во-вторых, отбор проб Монте-Карло

Предположим, мы можем образец от одной целевой вероятности к P (x) к серии образцов (частиц)(Что касается того, как генерировать образцы, распределенные из p (x), эта проблема расположена сначала), то эти образцы могут быть использованы для оценки ожидаемого значения определенных функций этого распределения. Например:

Вышеуказанный формат фактически рассчитывается для расчета ожидаемой проблемы, но она отличается только от функции интеграции.
Sampling Monte Carlo - заменить точки со средним, ищущим ожидания:

Это может понять его с точки зрения большой числа теоремы. Мы используем эту идею, чтобы указать разные F (x) для достижения цели оценки различных вещей. Например, необходимо оценить вес группы сверстников, без мужчин, есть 100 мужчин в большой выборке, 20 женщин, за меньшее количество вещей, мы берем 10 мужчин, 2 женщины, мера 12 человек в среднем Отказ Обратите внимание, что пропорциональная добыча здесь можно рассматривать как отбор проб из распределения вероятностей P (x).
Давайте возьмем еще один пример слегка академической точки:
Предполагается, что есть частиц однородной кости. Он предусматривается в игре, бросая кости подряд, как минимум 6 очков, появляющихся для победы. Теперь оцените вероятность победы. мы используемВ Nth Game результаты KTH BAK, K = 1 . 4. Для униформы, распределенных костей, каждая бросание повиновается равномерно распределено, а именно:
Интервал здесь состоит в том, чтобы взять номер, 1, 2, 3, 4, 5, 6, представляют 6 граней. Поскольку каждый бросок независимо распределен, целевое распределение P (x) здесь также является равномерным распределением.Отказ Одна играСлучайная точка в пространстве.
Для оценки вероятности выигрыша одна функция указания определяется в N-й игре:


При этом функция индикации I означает, что если условия выполнены, результат составляет 1, и результат составляет 0. Вернемся до этого вопроса, значение f () вот одна игра. Если в четыре бросания есть 6 бросков, результаты f () будут 1. Из этого предполагается, что ожидания победы в такой игре также является вероятностью выигрыша:
Когда количество выборки достаточно большим, вышеуказанная формула приближается к вероятности достижения реальной победы, увидев вышеупомянутую вероятность оценки, является целью вероятности оценки на угол метода Monte Carlo. Это то же самое, что и пример бросания монеты, и количество бросков можно использовать для оценки вероятности положительного или обратного внешнего вида.
Конечно, некоторые люди могут спросить, насколько велика предполагаемая ошибка, для этого вопроса, заинтересована, проверьте ссылки, которые я перечислю ссылку 2. ( И вновь увидеть информацию , Лично чувствую, что есть проблема или сначала поставлена, основные идеи будут следовать деталям.)
Далее вернитесь к нашей главной линии, как это в Монте-Карло?
Из вышеперечисленного мы знаем, что его можно использовать для оценки вероятности, а в предыдущем разделе соотношение вероятности байесовской после испытания следует использовать для решения проблемы этой интеграции, вы можете использовать выборку Monte Carlo вместо расчета. задняя вероятность.
Предположим, что он может быть выбираться из n образца из n по вероятности подраздела, затем расчет вероятности после испытания может быть представлен как:


Среди них, в этом методе Монте-Карло, мы определяемЭто функция Dirac Delta, которая аналогична значению вышеуказанного указания.
Увидев это, поскольку метод Monte Carlo может быть использован для непосредственного оценки последней вероятности, теперь используется вероятность после испытания, и как используется для отслеживания или фильтрации изображения? Для отслеживания или фильтрации изображений на самом деле он действительно хочет узнать ожидаемое значение текущего состояния:

То есть значение состояния частиц этих образцов составляет непосредственно среднее значение желаемого значения, то есть значение после фильтрации, которое является состоянием функции каждой частицы. Это фильтрация частиц, до тех пор, пока многие частицы выбираются из субтральной вероятности, результаты фильтрации получают с их состоянием.
Идея кажется простыми, но жизнь состоит в том, что вероятность пост-тестирования не знает, как отбора проб в распределении вероятностей подраздела! Так что не работайте напрямую, вы не можете это сделать. В это время он будет введен в эту проблему для решения этой проблемы.
В-третьих, важность
Невозможно отбора проб в распределении целевого распределения, просто отбора проб из известного распределения дискретизации, таких как q (x | y), так что вышеупомянутая проблема ожидания становится:

(2)


Поэтому (2) может быть дополнительно написано:


Приведенные выше желаемые расчеты могут быть решены Monte Carlo, то есть путем выборки N образцов.Среднее количество образцов используется в качестве желаемого желаемого, поэтому вышеупомянутое (3) может быть приблизительно:

Это вес после нормализации, а вес в (2) не нормализуется.
Обратите внимание, что вышеупомянутое (4) больше не (1) все состояние частиц напрямую, но взвешено и образуется. Различные частицы имеют свои соответствующие веса, и если правильность частицы значительна, она будет иллюстрировать, что частицы больше, чем частица.
Здесь я решил проблемы, которые не могут быть выбраны из вероятности подраздела, но вес каждой частицы непосредственно рассчитывается напрямую, эффективность низкая, поскольку каждый дополнительный образец P (x (K) | Y (1: K)) должен быть пересчитан, и это не хорошо рассчитать эту форму. Следовательно, вы можете избежать вычисления p (x (k) | y (1: k)), когда вы просите веса Лучшая форма состоит в том, чтобы рассчитать вес в процессе выталкивания, который является так называемой выборкой в последовательной важности (SIS), прототип фильтрации частиц.
Следующее запускает вывод веса с поддержкой W-включенной:

Предположим важность функций плотности вероятностиИндекс здесь равен 0: K, то есть фильтр частиц - это предполагаемое состояние состояния в прошлом. Предположим, его можно разложить как:

Рекурсивная форма функции плотности вероятностей подраздела может быть выражена как:

Среди них, чтобы выразить удобство, y (1: k) выражается y (k), и разница между y и Y. В то же время вывод вероятности после испытания в этой формуле и последнем разделе байесайской фильтрации одинаково, но предыдущий X (K) становится X (0: K) здесь, что отличается, что и BAYI Оценка нужна очки, а форма разложения вероятности после испытания не интегрирована.
Рекурсивная форма веса частиц может быть выражена как:


Обратите внимание, что вывод такой весовой формы должен быть получен в форме предыдущего (2), то есть никакой нормализации. В формуле государственной оценкиВес в этой формуле после нормализации, поэтому в практических применениях, после расчета рециркуляции, нормализация должна быть нормализована, и можно ввести (4) для расчета желаемого ожидания. В то же время молекулы в вышеуказанном (5) не очень знакомы. В предыдущем разделе мы уже сделали это, p (y | x), p (x (k) | x (k-1))) Форма на самом деле такая же, как форма распределения вероятностей шума в уравнении состояния, за исключением того, что среднее значение отличается. Следовательно, вероятность в формуле известна в формуле, и можно сказать, что в программировании можно сказать, что в программировании нет никаких сложностей. После того, как вес также доступен, вы можете получить фильтр SIS до тех пор, пока у вас небольшое резюме.
Четвертая, последовательная важность выборки (SIS) фильтр
В практических приложениях можно предположить, что важность распределения q () выполняется:

Эта гипотеза объясняет, что важность связана только со статусом X (K - 1) и измерения Y (k) в предыдущее время, то (5) можно преобразовать в:

После этого много предположений и после решения проблемы, наконец, есть, наконец, аналогичная фильтрация частиц.алгоритмОн является последовательным фильтром для отбора проб.
Этот алгоритм приведен в виде псевдо-кода:


(1) выборка:;

(2) в соответствии сВоспроизведение рассчитывает вес каждой частицы;
Вес частиц нормализуется. У частиц есть, а вес частиц может быть, а состояние взвешивания состояния каждых частиц могут быть выполнены с помощью (4).
Этот алгоритм является предшественником фильтрации частиц. Просто в практическом применении многие проблемы нашли многие проблемы, такие как отступление веса частицы, существует резомбистое, есть базовый алгоритм фильтрации частиц. Существует также проблема важности плотности вероятности Q () и т. Д. Все остаетсяСледующая главаРешать.
Интеллектуальная рекомендация
Поверните строку в целые числа
Тема Описание Преобразуйте строку в целое число (реализация функции integer.valueof (строка), но строка не совпадает 0), требуя функции библиотеки, которая нельзя использовать для преобразования целых.
Docker создает репликацию Redis Master-Slave
Centos установить докер быстрый старт докера Создать Dockerfile Поместите файл на сервер Linux, создайте папку / usr / docker / redis и поместите его в этот каталог Выполните следующий код в каталоге .

Установка GateOne на новом CentOS7
Установка GateOne на новом CentOS7 В последнее время исследуются такие инструменты, как WebSSH2, в настоящее время требуется встроить терминал ssh в веб-приложение и найти GateOne. GateOne - это веб-в.

Примечания к исследованию Qt4 (5), QWaitCondition of QThread Learning

Практические занятия: решения проблем системы управления обучением
Сразу после получения задания будет много трудностей и много проблем. Хорошо иметь проблему, а это значит, что вы можете получить новые знания. Неважно, есть ли проблемы, ключ в том, как их решить. пр.
Вам также может понравиться

искробезопасная практика (5) обратный индекс
задний план Поисковые системы обычно создают инвертированный индекс ключевых слов. Ключевое слово - индекс, за которым следуют веб-страницы, содержащие ключевое слово. На этот раз, используя данные мо.
Решение центра тяжести неправильного многоугольника
Справочник статей Во-первых, решение центра тяжести неправильных многоугольников 1.1 Метод расчета треугольника центра тяжести 1.2 Метод расчета площади треугольника 1.3 Метод расчета площади полигона.
Аннотация научной статьи по компьютерным и информационным наукам, автор научной работы — Парахневич А.В., Солонар А.С., Горшков С.А.
Рассмотрено описание нелинейной байесовской фильтрации численным методом Монте-Карло , показана суть метода фильтрации посредством выборки весовых коэффициентов , описаны особенности алгоритма перевыборки и построение обобщенного фильтра частиц на основе алгоритмов выборки весовых коэффициентов и перевыборки.
Похожие темы научных работ по компьютерным и информационным наукам , автор научной работы — Парахневич А.В., Солонар А.С., Горшков С.А.
Подходы к выбору значимой плотности вероятности в фильтрах частиц (particle filters) Методы фильтрации на основе многоточечной аппроксимации плотности вероятности оценки в задаче определения параметров движения цели при помощи измерителя с нелинейной характеристикой Определение местоположения источника радиоизлучения пассивной радиолокационной станцией методами марковской нелинейной фильтрации Использование последовательных методов Монте-Карло в задаче корреляционно-экстремальной навигации Методика анализа показателей качества устройства последовательного распознавания радиолокационных объектов i Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.Текст научной работы на тему «Фильтрация посредством выборки весовых коэффициентов. Обобщенный фильтр частиц (particle filter)»
ФИЛЬТРАЦИЯ ПОСРЕДСТВОМ ВЫБОРКИ ВЕСОВЫХ КОЭФФИЦИЕНТОВ. ОБОБЩЕННЫЙ ФИЛЬТР ЧАСТИЦ (PARTICLE FILTER)
А.В. ПАРАХНЕВИЧ, А С. СОЛОНАР, С.А. ГОРШКОВ
Военная академия Республики Беларусь Минск-57, 220057, Беларусь
Поступила в редакцию 22 декабря 2011
Рассмотрено описание нелинейной байесовской фильтрации численным методом Монте-Карло, показана суть метода фильтрации посредством выборки весовых коэффициентов, описаны особенности алгоритма перевыборки и построение обобщенного фильтра частиц на основе алгоритмов выборки весовых коэффициентов и перевыборки.
Ключевые слова: нелинейная фильтрация, метод Монте-Карло, выборка весовых коэффициентов.
Данная статья является второй в цикле статей, посвященных описанию фильтров частиц используемых в задачах нелинейной дискретной байесовской фильтрации. В первой статье [1] был рассмотрен метод численного интегрирования Монте-Карло 2 применительно к аппроксимации произвольных плотностей вероятности набором N случайных точек (частиц) и, как частный случай, аппроксимация апостериорных плотностей вероятности фильтруемых дискретно изменяющихся случайных марковских векторных параметров [5].
координат частиц ак для аппроксимации апостериорной ПВ вектора состояния ак размерностью па, описанного в [1], к алгоритму работы обобщенного фильтра частиц. В статье также рассматриваются проблемы вырождения частиц и пути их устранения.
Цель статьи: рассмотреть алгоритм фильтрации обобщенного фильтра частиц.
Задача: записать рекуррентный алгоритм работы обобщенного фильтра частиц, формирующего оценку измеряемого параметра ak.
Для решения поставленной задачи последовательно рассмотрим алгоритм выборки весовых коэффициентов SIS (Sequential Importance Sampling), опишем явление вырождения (как результат использования алгоритма SIS) и алгоритм перевыборки (Resampling; как средство предотвращения такого вырождения). Далее перейдем к рассмотрению алгоритма обобщенного фильтра частиц (SIR Particle Filter).
Фильтрация посредством выборки весовых коэффициентов
В основе алгоритма фильтрации частиц посредством выборки весовых коэффициентов лежит рекуррентное вычисление весов случайных отсчетов (частиц) и аппроксимация апостериорной плотности вероятности p(aк | ©к ) вектора состояния ак при наблюдении совокупного
вектора наблюдений 0к , где 0к = [1, 6, 7].
Последовательность операций для определения апостериорной ПВ на к-ом шаге измерения при использовании алгоритма выборки весовых коэффициентов представлена в псевдокоде на рис. 1. За этот алгоритм отвечает функция выборки весовых коэффициентов SIS, на вход которой с предыдущего шага измерения поступает набор из N частиц с соответствующими
Так как процедура фильтрации является рекуррентной, то вычисление текущей оценки апостериорной плотности вероятности осуществляется с использованием весов, экстраполированных с предыдущего на текущий шаг при помощи переходной значимой плотности вероятности (пункт 2 псевдокода на рис. 1), описанной в [1, 6, 12].
частиц и весов на [к-1) шаге);
- вектор наблюдаемых параметров на текущем шаге;
Вь,ход: кхГ, - аппроксимация апостериорной ПВ на текущем к-ом шаге
(совокупность частиц на к-ом шаге);
ик - оценка математического ожидания аппроксимируемой
2. Определение значений ненормированных весов частиц (for i=l. N):
4. Вычисление нормированных весов частиц (for/=l. W):
Рис. 1. Псевдокод алгоритма фильтрации посредством выборки весовых коэффициентов (SIS)
Наличие предполагаемого случайного маневра цели см в модели движения, заложенной в фильтр, будет приводить к тому, что координаты частиц с течением времени будут получать все больший разброс (наблюдается рост дисперсии ошибки аппроксимации ПВ). Число частиц, формирующих результирующую оценку математического ожидания апостериорной плотности вероятности, будет уменьшаться, и в конечном итоге оценку будет формировать лишь одна значимая частица, с весом, значительно превышающим веса остальных частиц. Это неизбежно будет приводить к увеличению ошибок фильтрации и срыву с сопровождения. В [6] возникновение таких ситуаций названо «явление вырождения». Графически вырождение можно пояснить рис. 2. Слева на рисунке представлена гауссова плотность вероятности аппроксимированная набором из N частиц на 1-м шаге наблюдения. На к-ом шаге (справа на рис. 2) по-
казан набор тех же N частиц, но значительно разбросанных по пространству за счет случайного маневра цели в модели движения, воздействующего на выборку k раз наблюдений. Легко заметить, что на к-ом шаге плотность вероятности аппроксимирует всего одна частица с преобладающим весом.
Рис. 2. Пример вырождения выборки за k шагов моделирования при N=1000
Явления вырождения невозможно избежать при рекуррентном использовании метода интегрирования Монте-Карло при решении задач последовательных решающих статистик, что явилось главной проблемой в развитии численных методов фильтрации [6]. В 1994 году Августином Конгом [13] в качестве меры вырождения было предложено использовать оценку эффективного размера выборки А^, показывающую число частиц, веса которых значительны [6, 13]:
где wk - нормированный вес.
Эффективный размер выборки лежит в диапазоне: 1 < N^ < N. Для обоснования этого утверждения достаточно рассмотреть два случая. В том случае, когда веса частиц одинаковые (т.е. w1k = 1/N для 7=1. N), эффективный размер выборки буде равен числу частиц: N= N .
В качестве средства для борьбы с явлением вырождения частиц используется перевыборка [6, 8, 11, 12, 14-17] - повторная генерация частиц на к-ом шаге по определенному правилу, описанному ниже. Перевыборку проводят каждый раз, когда наблюдается вырождение частиц (т.е. когда N^ становится ниже некоторого порога N\кг). Перевыборка позволяет перенести отсчеты из областей с малой вероятностью в области с большей вероятностью, что позволяет увеличивать число значимых отсчетов, существенно влияющих на результат аппроксимации (приводит к уменьшению дисперсии ошибки аппроксимации). Размер порога N йг в задачах фильтрации подбирается эмпирическим способом.
Для реализации операции группирования строятся две дискретные функции распреде-
мерно распределенное в интервале от 0 до 1/N случайное число (рис. 3,а). Функция с; используется в качестве пороговой. Она имеет вид совокупности ступенек различной высоты, которая равна весу 7-й значимой частицы w!k , перемежающихся почти ровными площадками, протяженность которых определяется числом вырожденных частиц на данном участке. На рис. 3 показан пример функций С; и и; для N=15.
Вначале определяются значения аргументов функции с;, соответствующие ступенькам. Они определяются номерами наиболее значимых частиц старой выборки. В рассматриваемом примере это 4, 8 и 13. Затем определяются аргументы значений функции и;, попадающих между ступеньками с1. Например, между ступенькой нулевой высоты и С4 находятся значения и! -и6. Между ступеньками С4 и с8 находятся величины и7-и10, а между с8 и сп-ип-и15. На основании серии описанных выше сравнений новым частицам с 1-й по 6-ю присваиваются координаты старой частицы с номером 4: а^ к = а, к , У = 1, 6 , с 7-й по 10-ю - координаты
старой частицы с номером 8: а ^ к = aoid, к , У = 7, 10 , с 11-й по 15-ю - координаты старой частицы номер 13: ак = аОи,к ,У = 11, 15 (рис. 3,6).
Рис. 3. Пояснение алгоритма перевыборки при числе частиц N=15: а - примеры функций cf и uf; б - результат выполнения операции группирования
Пример программной реализации алгоритма перевыборки с использованием порядковых статистик (order statistics) [3, 4, 15] приведен на рис. 3 в виде псевдокода.
\aoidk>wkij-i - аппроксимация апостериорной ПВ на к-ом шаге (совокупность
1. Расчет совокупной суммы весов (ССВ)
Инициализация ССВ на первом шаге: с1 = п^1; Определение значений ССВ (for /=2. N)\
2. Установка начальных значений:
Задать случайную начальную точку порога из равномерного закона u[]: iij
Задать начальное значение переменной инкремента: / = 1:
3. Для переменной j, циклически выполнить операции (for j=2r. rN):
Определить номер частицы исходной последовательности: rij = i Задать новую координату частицы: = аЦ%>к
4. Вернуть результат перевыборки в виде: \aJnswk,w£.
Рис. 4. Псевдокод алгоритма перевыборки (SIR)
Существуют и иные варианты реализации рассмотренной процедуры, например, стратифицированная и разностная перевыборки [11, 18, 19].
Обобщенный фильтр частиц
Рассмотрим пример, иллюстрирующий работу рекуррентного алгоритма обобщенного фильтра частиц для двух временных шагов при объеме выборки N=15 (рис. 5). Пусть на к-м шаге фильтрации имеется набор частиц ^ , которым аппроксимирована апостериорная
р(а к |0 к ) с координатами
110 О 7 120 О 8 130 Од 1Л0 010
i Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.6 42 5 3 1 1312 14 9 711 15 8 10
Рис. 5. Графическое представление работы фильтра частиц за 2 временных шага для числа частиц N=15
Алгоритм обобщенного фильтра частиц, учитывающий процедуру перевыборки, приведен в псевдокоде рис. 6. Как видно из данного рисунка, для запуска алгоритма перевыборки необходимо, чтобы оценка (1) (1) эффективного размер выборки Nоказалась меньше заранее
Несмотря на снижение негативного влияния эффекта вырождения на точность фильтрации, перевыборка порождает другие практические проблемы, например, ограничивает возможности по распараллеливанию алгоритма [4].
Как правило, оценка ПВ после перевыборки приводит к росту дисперсии ошибки этой оценки. Поэтому расчет математического ожидания вектора состояния ак производится до реализации процедуры перевыборки [6, 11, 12].
Таким образом, алгоритм фильтрации посредством выборки весовых коэффициентов, включает в себя генерацию частиц из значимой ПВ, рекуррентное вычисление весов с их последующей нормировкой, а также расчет математического ожидания аппроксимируемой ПВ.
Основная проблема рассматриваемого подхода - вырождение. Оно заключается в том, что со временем частицы «расползаются» по области определения вектора состояния и в пределах аппроксимируемой ПВ остается лишь малое их число, обладающее «значимыми» весами. Причина такого вырождения в том, что в модель изменения вектора состояния, как правило, вводятся случайные независимые от шага к шагу приращения (первые, вторые и т.д.) [20]. Дисперсия этих приращений связывается реальными физическими свойствами фильтруемых процессов. Например, при фильтрации параметров траекторий воздушных объектов устанавливается взаимосвязь с маневренными свойствами объекта и частотой поступления оценок координат (темпом обзора радиолокатора) [20].
(совокупность частиц на к-ом шаге) после перевыборки;
ак - оценка математического ожидания аппроксимируемой апостериорной ПВ до перевыборки 1. Фильтрация посредством выборки весовых коэффициентов (псевдокод 1):
2. Вычислить эффективный размер выборки 1
- Проверить выполнение условия осуществления перевыборки:
- Если условие выполнено - перейти к пункту 3, если не выполнено - к пункту 4 то произвести перевыборку (псевдокод 2):
4. Выдать результат фильтрации на текущем шаге в виде вектора: | \и!к,\ук 1 =1
Рис. 6. Псевдокод обобщенного фильтра частиц
Для уменьшения влияния эффекта вырождения используют варианты процедур перевыборки. Идея перевыборки заключается в том, чтобы сгруппировать все частицы устаревшей вырождающейся выборки только в окрестности наиболее значимых частиц, с последующим приданием им одинаковых весов. При последующих шагах экстраполяции стянутые в локальные области частицы перераспределяются в пределах всей фильтруемой ПВ за счет случайных приращений к значениям их координат.
Обобщенный фильтр частиц включает в себя процедуру перевыборки, которая запускается всякий раз, когда число значимых частиц падает ниже определенного порога.
SEQUENTIAL IMPORTANCE SAMPLING FILTERING. GENERIC PARTICLE FILTER
A.V. PARAKHNEVICH, A.S. SOLONAR, S.A. GORSHKOV
Mathematical description of non-linear bayesian filtering using Monte-Carlo method is spent, the basis of Sequential Importance Sampling (SIS) filtering method is shown, features of resampling algorithm and constructing Generic particle filter by using resampling in the report are descrited.
1. Парахневич А.В., СолонарА.С., Горшков С.А. / Докл. БГУИР. 2012. №1(62). С. 22-28.
2. Hammersley J.M., Morton K. W. // Journal of the Royal Statistical Society B. 1954. Vol. 16. P. 23-38.
3. Соболь И.М. Численные методы Монте-Карло. М., 1973.
4. Gordon N.J., SalmondD.J., Smith A.F.M. // IEEE Proceedings-F. 1993. Vol. 140, №2. P. 107-113.
5. Daum F. // IEEE A&E Systems Magazine. 2005. Vol. 20, №8. P. 57-69.
6. Ristic B., Arulampalam S., Gordon N. Beyond the Kalman Filter. Particle filters for tracking applications. London, 2004.
7. Gordon N. // IEEE Transactions on Aerospace and Electronic systems. 1997.
8. DoucetA., Godsill S., Andrieu A. // Statistics and Computing. 2000. Vol. 10, №3. P. 197-208.
9. Doucet A., De Freitas N., Gordon N.J. // New York: Springer-Verlag, Series Statistics for Engineering and Information Science. 2001. P. 620.
10. Andrieu C., Doucet A. // Journal Royal Statistical Society B. 2000.
11. Bolic M. // Architectures for Efficient Implementation of Particle Filters. Dissertation of Ph. D. Stony Brook University. 2004.
12. Chen Z. // IEEE A&E Systems Magazine. 2011. №4. P. 69.
14. PittM., ShephardN. // Journal of the American Statistical association. 1999. P. 590-599.
15. Marrs A., Maskell S., Bar-Shalom Y. // SPIE. 2002.Vol. 4728.
16. Merwe R. V.D., Doucet A., Freitas N. et al. // The Unscented Particle Filter. 2000.
17. Arulampalam M.S, Maskell S., Gordon N. et al. // IEEE Trans. Signal Processing. 2002. Vol. 50. P. 174-188.
18. Gustafsson F., Gunnarsson F., Bergman N. // IEEE Transactions on Signal Processing. 2002. P. 13.
19. Hlinka O, Sluciak O, Hlawatsch F. // IEEE ICASSP. 2011. P. 3756-3759.
20. ШирманЯ.Д., Багдасарян С.Т., Маляренко А.С. Радиоэлектронные системы: Основы построения и теория. М., 2007.
Измерение значений
Фильтры
Цифровые (программные) фильтры позволяют отфильтровать различные шумы. В следующих примерах будут показаны некоторые популярные фильтры. Все примеры оформлены как фильтрующая функция, которой в качестве параметра передаётся новое значение, и функция возвращает фильтрованную величину. Некоторым функциям нужны дополнительные настройки, которые вынесены как переменные. Важно: практически каждый фильтр можно настроить лучше, чем показано на примерах с графиками. На примерах фильтр специально настроен не идеально, чтобы можно было оценить особенность работы алгоритма каждого из фильтров.
Среднее арифметическое
Однократная выборка
Среднее арифметическое вычисляется как сумма значений, делённая на их количество. Первый алгоритм именно так и работает: в цикле суммируем всё в какую-нибудь переменную, потом делим на количество измерений. Вуаля!
Особенности использования
Растянутая выборка
Отличается от предыдущего тем, что суммирует несколько измерений, и только после этого выдаёт результат. Между расчётами выдаёт предыдущий результат:
Особенности использования
Бегущее среднее арифметическое
Данный алгоритм работает по принципу буфера, в котором хранятся несколько последних измерений для усреднения. При каждом вызове фильтра буфер сдвигается, в него добавляется новое значение и убирается самое старое, далее буфер усредняется по среднему арифметическому. Есть два варианта исполнения: понятный и оптимальный:
Особенности использования
Экспоненциальное бегущее среднее
Особенности использования
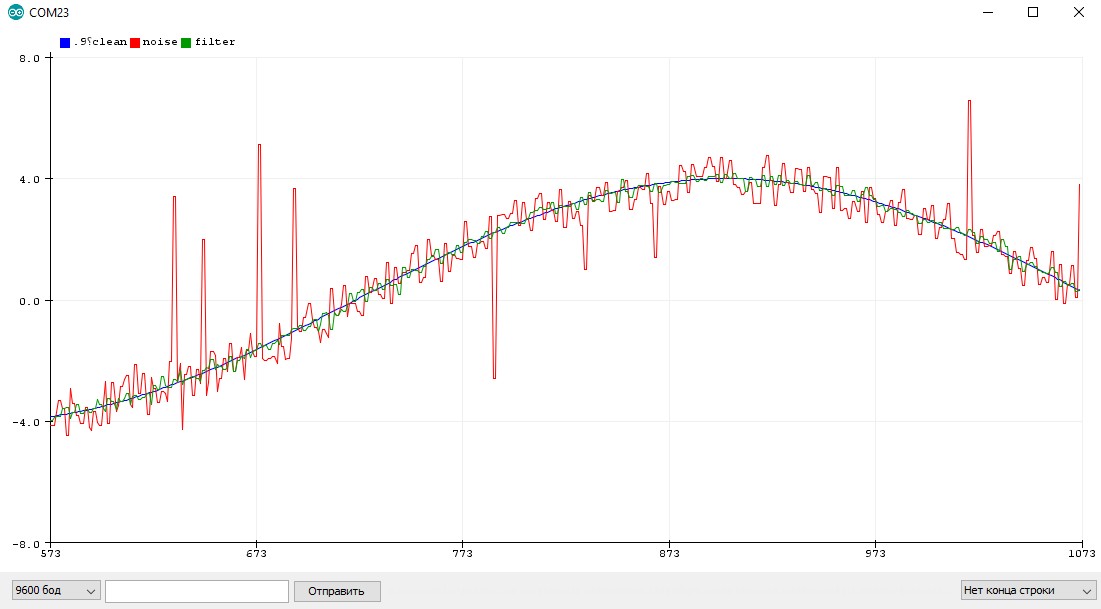
Вот так бегущее среднее справляется с равномерно растущим сигналом + случайные выбросы. Синий график – реальное значение, красный – фильтрованное с коэффициентом 0.1, зелёное – коэффициент 0.5.
Пример с шумящим синусом
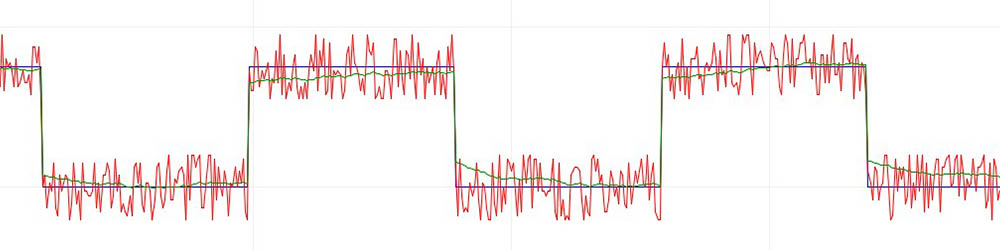
Пример с шумным квадратным сигналом, на котором видно запаздывание фильтра:

Адаптивный коэффициент
Простой пример
Код выводит в порт реальное и фильтрованное значение. Можно подключить к А0 потенциометр и покрутить его, наблюдая за графиком.
Медианный фильтр
Медианный фильтр тоже находит среднее значение, но не усредняя, а выбирая его из представленных. Алгоритм для медианы 3-го порядка (выбор из трёх значений) выглядит так:
Мой постоянный читатель Андрей Степанов предложил сокращённую версию этого алгоритма, которая занимает одну строку кода и выполняется чуть быстрее за счёт меньшего количества сравнений:
Можно ещё визуально сократить за счёт использования функций min() и max() :
Для удобства использования можно сделать функцию, которая будет хранить в себе буфер на последние три значения и автоматически добавлять в него новые:
Большое преимущество медианного фильтра заключается в том, что он ничего не вычислят, а просто сравнивает числа. Это делает его быстрее фильтров других типов!
Медиана для большего окна значений описывается весьма внушительным алгоритмом, но я предлагаю пару более оптимальных вариантов:

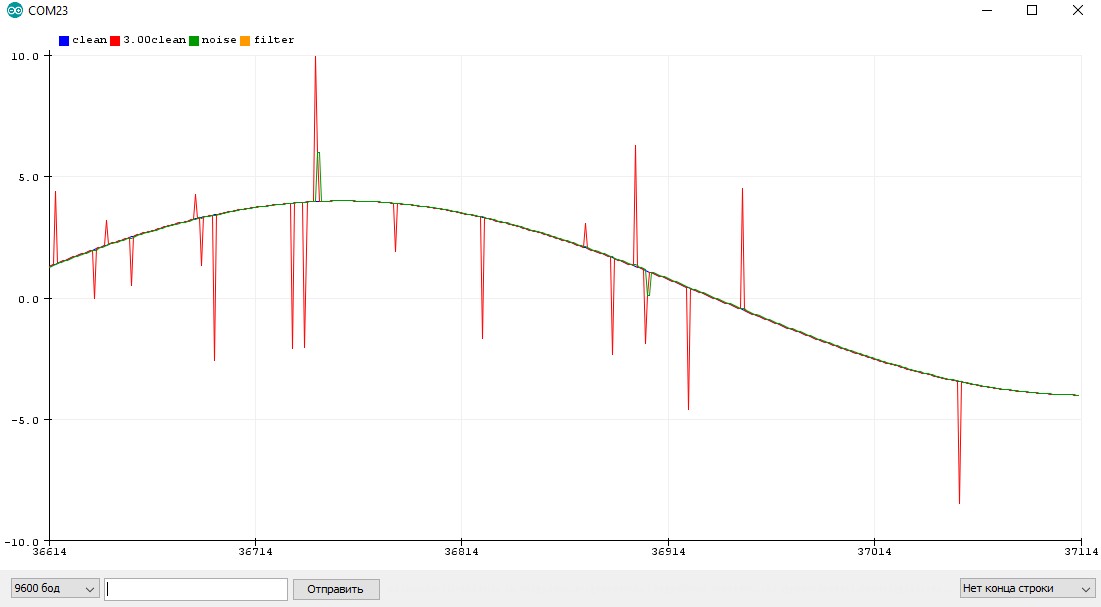
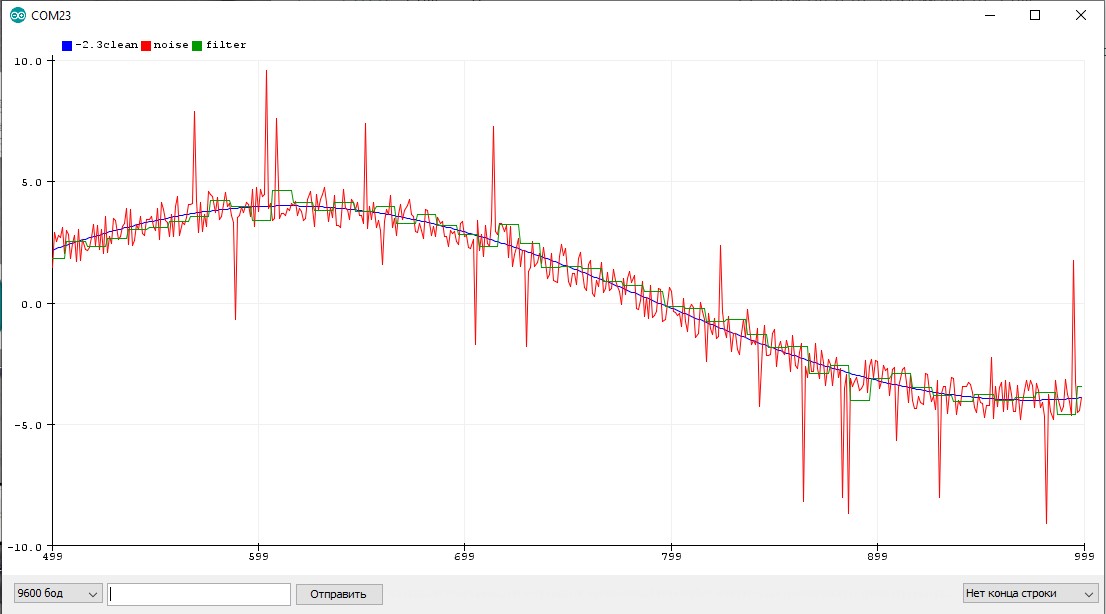
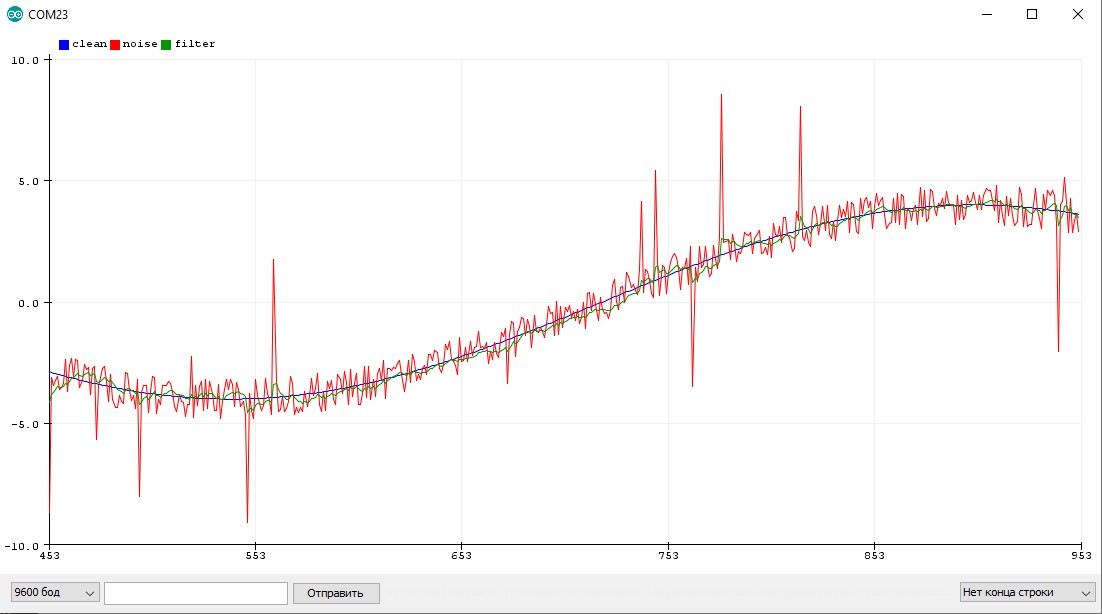
Данный алгоритм я нашёл на просторах Интернета, источник потерял. В фильтре настраивается разброс измерения (ожидаемый шум измерения), разброс оценки (подстраивается сам в процессе работы фильтра, можно поставить таким же как разброс измерения), скорость изменения значений (0.001-1, варьировать самому).
Особенности использования
- Хорошо фильтрует и постоянный шум, и резкие выбросы
- Делает только одно измерение за раз, не блокирует код на длительный период
- Слегка запаздывает, как бегущее среднее
- Подстраивается в процессе работы
- Чем чаще измерения, тем лучше работает
- Алгоритм весьма тяжёлый, вычисление длится
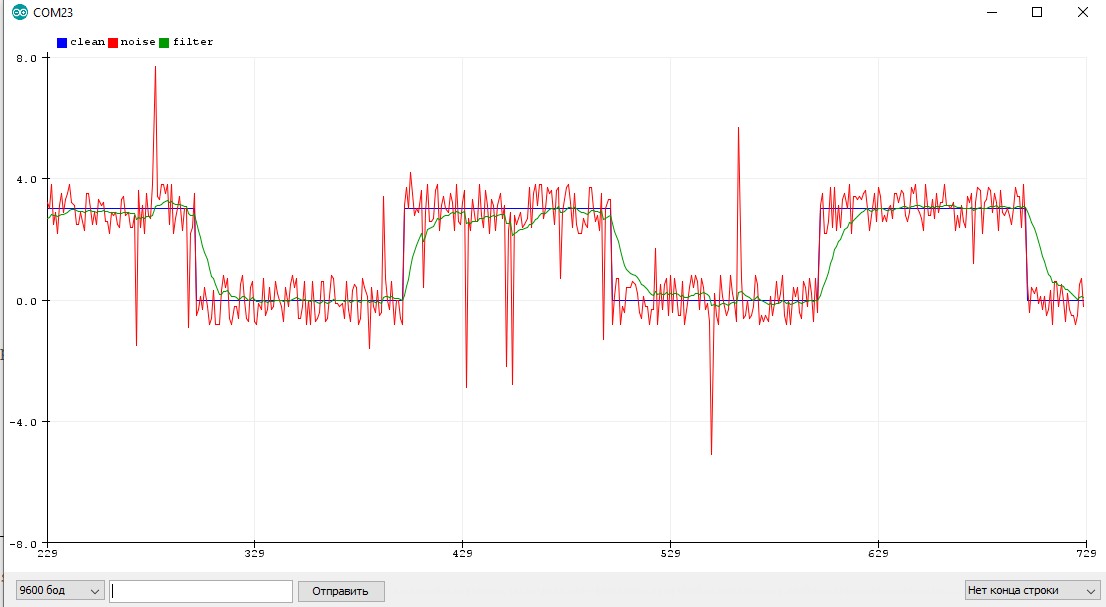
Альфа-Бета фильтр
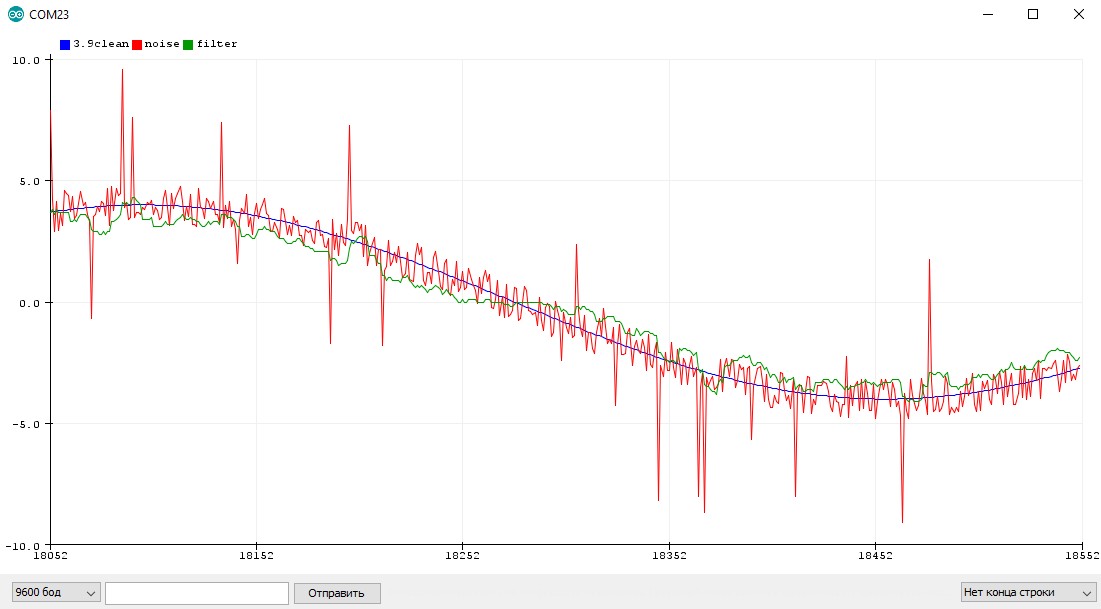
AB фильтр тоже является одним из видов фильтра Калмана, подробнее можно почитать можно на Википедии.
Особенности использования
- Хороший фильтр, если правильно настроить
- Но очень тяжёлый!
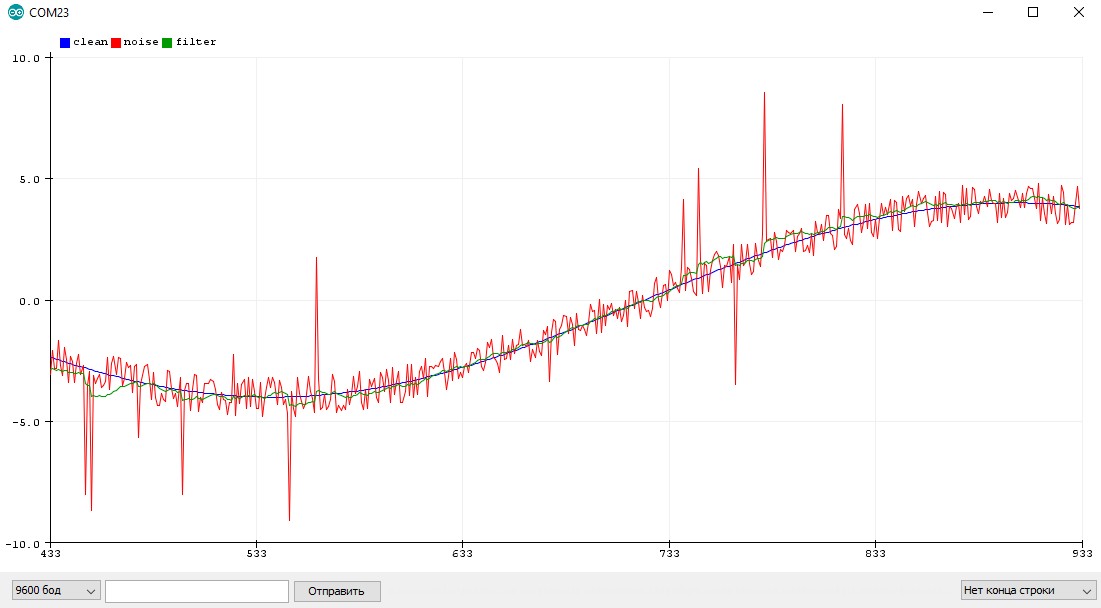
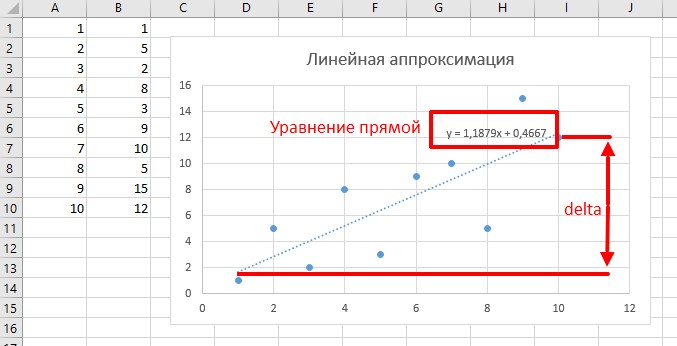
Метод наименьших квадратов
Особенности использования
- В моей реализации принимает два массива и рассчитывает параметры линии, равноудалённой от всех точек
Быстрые целочисленные фильтры
Все рассмотренные выше фильтры не могут похвастаться высокой скоростью выполнения вычислений: куча сложений, деление, работа с float и всё такое. Иногда бывает нужно максимально быстро отфильтровать например целочисленный сигнал с АЦП, и тут на помощь приходят шустрые целочисленные фильтры. Основную информацию по точной и осмысленной настройке фильтров можно почитать на easyelectronics, а мы с вами разберём три простых алгоритма, которые являются быстрыми аналогами бегущего среднего. За счёт целочисленных вычислений фильтры имеют небольшое отклонение от реального сигнала (см. графики ниже).
Первый
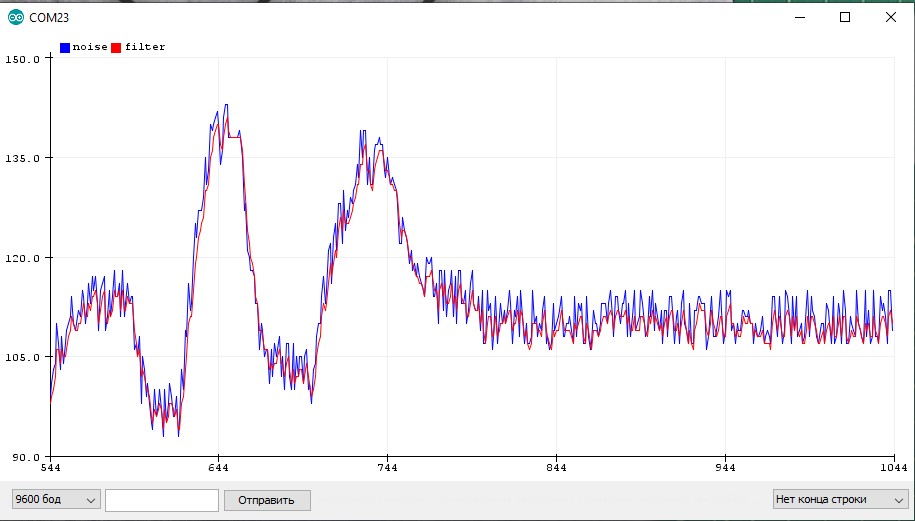
Фильтр не имеет настроек, состоит из сложения и двух сдвигов, выполняется моментально. Но и фильтрует совсем чуть-чуть:
Второй
Коэффициенты у этого фильтра выбираются следующим образом:
Например k = 4, значит A+B = 16. Хотим плавный фильтр, принимаем A=14, B=16: filt = (14 * filt + 2 * signal) >> 4;
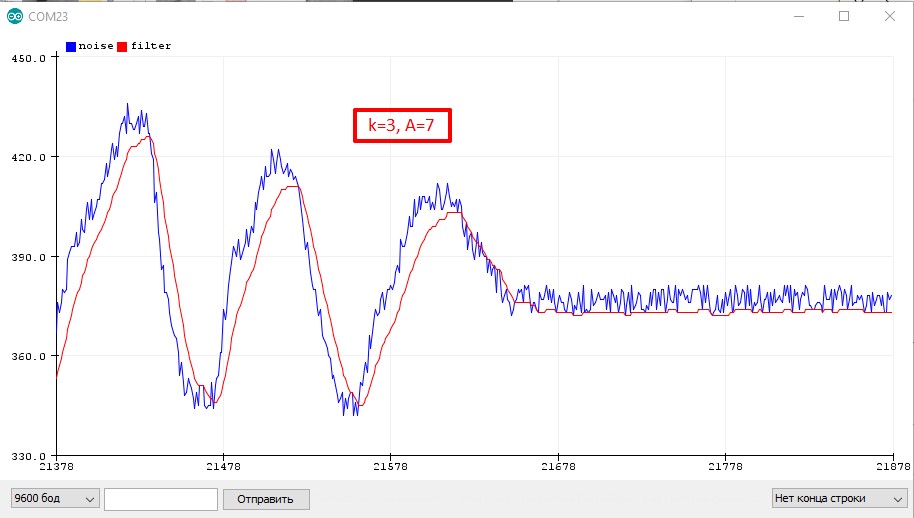
Третий
Третий алгоритм вытекает из второго: коэффициент B принимаем равным 1 и экономим одно умножение: filt = (A * filt + signal) >> k;
Тогда коэффициенты выбираются так:
Какой фильтр выбрать?
Библиотека GyverFilters
Библиотека содержит все описанные выше фильтры в виде удобного инструмента для Arduino. Документацию и примеры к библиотеке можно посмотреть здесь.
- GFilterRA – компактная альтернатива фильтра экспоненциальное бегущее среднее (Running Average)
- GMedian3 – быстрый медианный фильтр 3-го порядка (отсекает выбросы)
- GMedian – медианный фильтр N-го порядка. Порядок настраивается в GyverFilters.h – MEDIAN_FILTER_SIZE
- GABfilter – альфа-бета фильтр (разновидность Калмана для одномерного случая)
- GKalman – упрощённый Калман для одномерного случая (на мой взгляд лучший из фильтров)
- GLinear – линейная аппроксимация методом наименьших квадратов для двух массивов
Видео
Читайте также:

