Градиентный метод с постоянным шагом в эксель
Обновлено: 07.07.2024
В первой части я забыл упомянуть, что если случайно сгенерированные данные не по душе, то можно взять любой подходящий пример отсюда. Можно почувствовать себя ботаником, виноделом, продавцом. И все это не вставая со стула. В наличии множество наборов данных и одно условие — при публикации указывать откуда взял данные, чтобы другие смогли воспроизвести результаты.
Градиентный спуск
В прошлой части был показан пример вычисления параметров линейной регрессии с помощью метода наименьших квадратов. Параметры были найдены аналитически — , где — псевдообратная матрица. Это решение наглядное, точное и короткое. Но есть проблема, которую можно решить численно. Градиентный спуск — метод численной оптимизации, который может быть использован во многих алгоритмах, где требуется найти экстремум функции — нейронные сети, SVM, k-средних, регрессии. Однако проще его воспринять в чистом виде (и проще модифицировать).
Проблема заключается в том, что вычисление псевдообратной матрицы очень затратно: 2 умножения по , нахождение обратной матрицы — , умножение матрицы вектор , где n — количество элементов в матрице A (количество признаков * количество элементов в тестовой выборке) Если количество элементов в матрице A велико (> 10^6 — например), то даже если в наличии 10000 ядер, нахождение решения аналитически может затянуться. Также первая производная может оказаться нелинейной, что усложнит решение, аналитического решения может не оказаться вовсе или данные могут просто не влезть в память и потребуется итеративный алгоритм. Бывает, что в плюсы записывают и то, что численное решение не идеально точное. В связи с этим функцию стоимости минимизируют численными методами. Задачу нахождения экстремума называют задачей оптимизации. В этой части я остановлюсь на методе оптимизации, который называется градиентный спуск.
Не будем отходить от линейной регрессии и МНК и обозначим функцию потерь как — она осталась неизменной. Напомню, что градиент — это вектор вида , где — это частная производная. Одним из свойств градиента является то, что он указывает направление, в котором некоторая функция f возрастает больше всего. Доказательство этого следует из определения производной. Пара доказательств. Возьмем некоторую точку a — в окрестности этой точки функция F должна быть определена и дифференцируема, тогда вектор антиградиента будет указывать на направление, в котором функция F убывает быстрее всего. Отсюда делается вывод, что в некоторой точке b, равной , при некотором малом значение функции будет меньше либо равным значению в точке а. Можно представить это, как движение вниз по холму — сделав шаг вниз, текущая позиция будет ниже, чем предыдущая. Таким образом, на каждом следующем шаге высота будет как минимум не увеличиваться. Формальное определение. Исходя из этих определений можно получить формулу для нахождения неизвестных параметров (это просто переписанная версия формулы выше):


— это шаг метода. В задачах машинного обучения его называют скоростью обучения.
Метод очень прост и интуитивен, возьмем простой двумерный пример для демонстрации:
Необходимо минимизировать функцию вида . Минимизировать значит найти при каком значении функция принимает минимальное значение. Определим последовательность действий:
1) Необходима производная по :
2) Установим начальное значение = 0
3) Установим размер шага — попробуем несколько значений — 0.1, 0.9, 1.2, чтобы посмотреть как этот выбор повлияет на сходимость.
4) 25 раз подряд выполним указанную выше формулу: Так как неизвестный параметр только один, то и формула только одна.
Код крайне прост. Исключая определение функций, весь алгоритм уместился в 3 строки:
Весь процесс можно визуализировать примерно так (синяя точка — значение на предыдущем шаге, красная — текущее):
Или же для шага другого размера:
При значении, равном 1.2, метод расходится, каждый шаг опускаясь не ниже, а наоборот выше, устремляясь в бесконечность. Шаг в простой реализации подбирается вручную и его размер зависит от данных — на каких-нибудь ненормализованных значениях с большим градиентом и 0.0001 может приводить к расхождению.
Вот еще пример с «плохой» функцией. В первой анимации метод также расходится и будет долго блуждать по холмам из-за слишком высокого шага. Во втором случае был найден локальный минимум и варьируя значение скорости не получится заставить метод найти минимум глобальный. Этот факт является одним недостатков метода — он может найти глобальный минимум только если функция выпуклая и гладкая. Или если повезет с начальными значениями.

Плохая функция:
Также возможно рассмотреть работу алгоритма на трехмерном графике. Часто рисуют только изолинии какой-то фигуры. Я взял простой параболоид вращения: . В 3D выглядит он так: , а график с изолиниями — «вид сверху».
Также обратите внимание, что все линии градиента, направлены перпендикулярно изолиниям. Это означает, что двигаясь в сторону антиградиента, не получится за один шаг сразу же прыгнуть в минимум — градиент указывает совсем не туда.

После графического пояснения, найдем формулу для вычисления неизвестных параметров линейной регрессии с МНК.

Если бы количество элементов в тестовой выборке было равно единице, то формулу можно было бы так и оставить и считать. В случае, когда в наличии n элементов алгоритм выглядит так:

Повторять v раз
для каждого j одновременно.
>, где n — количество элементов в обучающей выборке, v — количество итераций
Требование одновременности означает, что производная должна быть вычислена со старыми значениями theta, не стоит вычислять сначала отдельно первый параметр, затем второй и т.д., потому что после изменения первого параметра отдельно, производная также изменит свое значение. Псевдокод одновременного изменения:
Если вычислять значения параметров по одиночке, то это уже будет не градиентный спуск. Допустим, у нас трехмерная фигура и если вычислять параметры один за одним, то можно представить этот процесс как движение только по одной координате за раз — один шажок по x координате, затем шажок по y координате и т.д. ступеньками, вместо движения в сторону вектора антиградиента.
Приведенный выше вариант алгоритма называют пакетный градиентный спуск. Количество повторений можно заменить на фразу «Повторять, пока не сойдется». Эта фраза означает, что параметры будут корректироваться до тех пор, пока предыдущее и текущее значения функции стоимости не сравняются. Это значит, что локальный или глобальный минимум найден и дальше алгоритм не пойдет. На практике равенства достичь невозможно и вводится предел сходимости . Его устанавливают какой-нибудь малой величиной и критерием остановки является то, что разность предыдущего и текущего значений меньше предела сходимости — это значит, что минимум достигнут с нужной, установленной точностью. Выше точности (меньше ) — больше итераций алгоритма. Выглядит это как-то так:
Так как пост неожиданно растянулся, я бы хотел его на этом завершить — в следующей части я продолжу разбор градиентного спуска для линейной регрессии с МНК.
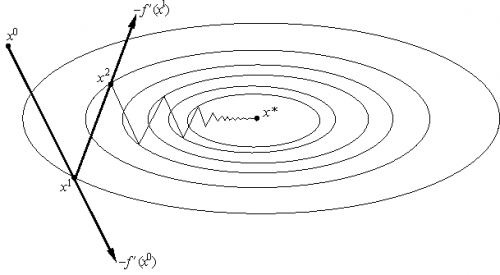
В методах поиска первого порядка в качестве направления поиска максимума целевой функции Ф(Х) выбирается вектор градиент целевой функции grad (Ф(Х k )), для поиска минимума - вектор антиградиент -grad (Ф(Х k )). При этом используется свойство вектора градиента указывать направление наискорейшего изменения функции:

Для изучения методов поиска первого порядка важно также следующее свойство: вектор градиент grad (Ф(Х k )) направлен по нормали к линии уровня функции Ф(Х) в точке Х k (см. рис. 2.4). Линии уровня - это кривые, на которых функция принимает постоянное значение (Ф(Х) = соnst).
В данной главе мы рассмотрим 5 модификаций градиентного метода:
градиентный метод с постоянным шагом,
градиентный метод с дроблением шага,
метод наискорейшего спуска,
двухуровневый адаптивный метод.
Градиентный метод с постоянным шагом
В градиентном методе с постоянным шагом исходными данными являются требуемая точность , начальная точка поиска Х 0 и шаг поиска h.
Получение новых точек производится по формуле:

Формула (2.7) применяется, если для функции Ф(Х) необходимо найти минимум. Если же задача параметрической оптимизации ставится как задача поиска максимума, то для получения новых точек в градиентном методе с постоянным шагом используется формула:

Каждая из формул (2.6), (2.7) является векторным соотношением, включающим n уравнений. Например, с учетом Х k+1 = ( x1 k+1 , x2. k+1 ,…,xn k+1 ), Х k = ( x1 k , x2. k ,…,xn k ) формула (2.6) примет вид:

или в скалярном виде

В общем виде (2.9) можно записать:

В качестве условия прекращения поиска во всех градиентных методах используется, как правило, комбинация двух условий: Ф(X k+1 ) - Ф(X k ) или


В градиентном методе можно несколько сократить число итераций, если научиться избегать ситуаций, когда несколько шагов поиска выполняются в одном и том же направлении.
Градиентный метод с дроблением шага
В градиентном методе с дроблением шага процедура подбора величины шага на каждой итерации реализуется следующим образом.
Исходными данными являются требуемая точность , начальная точка поиска Х 0 и начальная величина шага поиска h (обычно h = 1). Получение новых точек производится по формуле:

где hk - величина шага на k-ой итерации поиска, при hk должно выполняться условие:

Если величина hk такова, что неравенство (2.13) не выполнено, то производится дробление шага до тех пор, пока данное условие не будет выполнено. Дробление шага выполняется по формуле hk = hk , где 0 1.Такой подход позволяет сократить число итераций, но затраты на проведение одной итерации при этом несколько возрастают.
Метод наискорейшего спуска
В методе наискорейшего спуска на каждой итерации градиентного метода выбирается оптимальный шаг в направлении градиента.
Исходными данными являются требуемая точность , начальная точка поиска Х 0 .
Получение новых точек производится по формуле:

то есть выбор шага производится по результатам одномерной оптимизации по параметру h.
Основная идея метода наискорейшего спуска заключается в том, что на каждой итерации метода выбирается максимально возможная величина шага в направлении наискорейшего убывания целевой функции, то есть в направлении вектора-антиградиента функции Ф(Х) в точке Х k ( рис. 2. 4).

При выборе оптимальной величины шага необходимо из множества ХМ = < Х Х = Х k - hgrad Ф(Х k ), h[0,) >точек, лежащих на векторе градиенте функции Ф(Х), построенном в точке Х k , выбрать ту, где функция Ф(h) = Ф(Х k - h grad Ф(Х k )) принимает минимальное значение.
На практике целевые функции являются гораздо более сложными, линии уровня также имеют сложную конфигурацию, но в любом случае справедливо следующее: из всех градиентных методов в методе наискорейшего спуска наименьшее число итераций, но некоторую проблему представляет поиск оптимального шага численными методами, так как в реальных задачах, возникающих при проектировании РЭС, применение классических методов нахождения экстремума практически невозможно.
В этой статье речь пойдет о методах решения задач математической оптимизации, основанных на использовании градиента функции. Основная цель — собрать в статье все наиболее важные идеи, которые так или иначе связаны с этим методом и его всевозможными модификациями.

Примечание от автора
На момент написания я защитил диссертацию, задача которой требовала от меня глубокое понимание теоретических основно методов математической оптимизации. Тем не менее, у меня до сих пор (как и у всех) расплываются глаза от страшных длинных формул, поэтому я потратил немалое время, чтобы вычленить ключевые идеи, которые бы характеризовали разные вариации градиентных методов. Моя личная цель — написать статью, содержащую минимальное количество информации, необходимое для более менее подробного понимания тематики. Но будьте готовы, без формул так или иначе не обойтись.
Постановка задачи
Прежде чем описывать метод, следует сначала описать задачу, а именно: «Даны множество и функция , требуется найти точку , такую что для всех », что обычно записывается например вот так
В теории обычно предполагается, что — дифференцируемая и выпуклая функция, а — выпуклое множество (а еще лучше, если вообще ), это позволяет дать какие-то гарантии успешности применения градиентного спуска. На практике градиентный спуск успешно применяется даже когда у задачи нет ни одного из вышеперечисленных свойств (пример дальше в статье).
Немного математики
Допустим пока что нам нужно просто найти минимум одномерной функции
Еще в 17 веке Пьером Ферма был придуман критерий, который позволял решать простые задачи оптимизации, а именно, еcли — точка минимума , то
где — производная . Этот критерий основан на линейном приближении
Чем ближе к , чем точнее это приближение. В правой части — выражение, которое при может быть как больше так и меньше — это основная суть критерия. В многомерном случае аналогично из линейного приближения (здесь и далее — стандартное скалярное произведение, форма записи обусловлена тем, что скалярное произведение — это то же самое, что матричное произведение вектор-строки на вектор-столбец) получается критерий
Величина — градиент функции в точке . Также равенство градиента нулю означает равенство всех частных производных нулю, поэтому в многомерном случае можно получить этот критерий просто последовательно применив одномерный критерий по каждой переменной в отдельности.
Стоит отметить, что указанные условия являются необходимыми, но не достаточными, самый простой пример — 0 для и
Этот критерий является достаточным в случае выпуклой функции, во многом из-за этого для выпуклых функций удалось получить так много результатов.
Квадратичные функции
Для экономии места (да и чтобы меньше возиться с индексами) такую функцию обычно записывают в матричной форме:
где , , — матрица, у которой на пересечении строки и столбца стоит величина
( при этом получается симметричной — это важно). Далее. при упомянании квадратичной функции я буду иметь указанную выше функцию.
Зачем я об этом рассказываю? Дело в том, что квадратичные функции важны в оптимизации по двум причинам:
- Они тоже встречаются на практике, например при построении линейной регрессии методом наименьших квадратов
- Градиент квадратичной функции — линейная функция, в частности для функции выше
Или в матричной форме
Полезные свойства градиента
Хорошо, мы вроде бы выяснили, что если функция дифференцируема (у нее существуют производные по всем переменным), то в точке минимума градиент должен быть равен нулю. А вот несет ли градиент какую-нибудь полезную информацию в случае, когда он отличен от нуля?
Попробуем пока решить более простую задачу: дана точка , найти точку такую, что . Давайте возьмем точку рядом с , опять же используя линейное приближение . Если взять , то мы получим
Аналогично, если , то будет больше (здесь и далее ). Опять же, так как мы использовали приближение, то эти соображения будут верны только для малых . Подытоживая вышесказанное, если , то градиент указывает направление наибольшего локального увеличения функции.
Вот два примера для двумерных функций. Такого рода картинки можно часто увидеть в демонстрациях градиентного спуска. Цветные линии — так называемые линии уровня, это множество точек, для которых функция принимает фиксированное значений, в моем случае это круги и эллипсы. Я обозначил синими линии уровня с более низким значением, красными — с более высоким.


Обратите внимание, что для поверхности, заданной уравнением вида , задает нормаль (в простонародии — перпендикуляр) к этой поверхности. Также обратите внимание, что хоть градиент и показывает в направлении наибольшего увеличения функции, нет никакой гарантии, что по направлению, обратному к градиенту, можно найти минимум (пример — левая картинка).
Градиентный спуск
До базового метода градиентного спуска остался лишь малый шажок: мы научились по точке получать точку с меньшим значением функции . Что мешает нам повторить это несколько раз? По сути, это и есть градиентный спуск: строим последовательность
Величина называется размером шага (в машинном обучении — скорость обучения). Пару слов по поводу выбора : если — очень маленькие, то последовательность медленно меняется, что делает алгоритм не очень эффективным; если же очень большие, то линейное приближение становится плохим, а может даже и неверным. На практике размер шага часта подбирают эмпирически, в теории обычно предполагается липшицевость градиента, а именно, если
для всех , то гарантирует убывание .
Анализ для квадратичных функций
Если — симметричная обратимая матрица, , то для квадратичной функции точка является точкой минимума (UPD. при условии, что этот минимум вообще существует — не принимает сколько угодно близкие к значения только если положительно определена), а для метода градиентного спуска можно получить следующее
где — единичная матрица, т.е. для всех . Если же , то получится
Выражение слева — расстояние от приближения, полученного на шаге градиентного спуска до точки минимума, справа — выражение вида , которое сходится к нулю, если (условие, которое я писал на в предыдущем пункте как раз это гарантирует). Эта базовая оценка гарантирует, что градиентный спуск сходится.
Модификации градиентного спуска
Теперь хотелось бы рассказать немного про часто используемые модификации градиентного спуска, в первую очередь так называемые
Инерционные или ускоренные градиентные методы
Все методы такого класса выражаются в следующем виде
Последнее слагаемое характеризует эту самую «инерционность», алгоритм на каждом шаге старается двигаться против градиента, но при этом по инерции частично двигается в том же направлении, что и на предыдущей итерации. Такие методы обладают двумя важными свойствами:
- Они практически не усложняют обычный градиентный спуск в вычислительном плане.
- При аккуратном подборе такие методы на порядок быстрее, чем обычный градиентный спуск даже с оптимально подобранным шагом.
Метод тяжелого шарика — самый простой инерционный метод, но не самый первый. При этом, на мой взгляд, самый первый метод довольно важен для понимания сути этих методов.
Метод Чебышева
Да да, первый метод такого типа был придуман еще Чебышевым для решения систем линейных уравнений. В какой-то момент при анализе градиентного спуска было получено следующее равенство
где — некоторый многочлен степени . Почему бы не попробовать подобрать таким образом, чтобы было поменьше? Один уз универсальных многочленов, которые меньше всего отклоняются от нуля — многочлен Чебышева. Метод Чебышева по сути заключается в том, чтобы подобрать параметры спуска так, чтобы был многочленом Чебышева. Есть правда одна небольшая проблема: для обычного градиентного спуска это просто невозможно. Однако для инерционных методов это оказывается возможным. В основном это происходит из-за того, что многочлены Чебышева удовлетворяют рекуррентному соотношению второго порядка
поэтому их невозможно построить для градиентного спуска, который вычисляет новое значение лишь по одному предыдущему, а для инерционных становится возможным за счет того, что используется два предыдущих значения. При этом оказывается, что сложность вычисления не зависит ни от , ни от размера пространства .
Метод сопряженных градиентов
Еще один очень интересный и важный факт (следствие теоремы Гамильтона-Кэли): для любой квадратной матрицы размера существует многочлен степени не больше , для которого . Чем это интересно? Все дело в том же равенстве
Если бы мы могли подбирать размер шага в градиентном спуске так, чтобы получать именно этот обнуляющий многочлен, то градиентный спуск сходился бы за фиксированное число итерации не большее размерности . Как уже выяснили — для градиентного спуска мы так делать не можем. К счастью, для инерционных методов — можем. Описание и обоснование метода довольно техническое, я ограничусь сутью:на каждой итерации выбираются параметры, дающие наилучший многочлен, который можно построить учитывая все сделанные до текущего шага измерения градиента. При этом
- Одна итерация градиентного спуска (без учета вычислений параметров) содежит одно умножение матрицы на вектор и 2-3 сложения векторов
- Вычисление параметров также требует 1-2 умножение матрицы на вектор, 2-3 скалярных умножения вектор на вектор и несколько сложений векторов.
Метод сопряженных градиентов хорошо работает и в случае, если не является квадратичной функцией, но при этом уже не сходится за конечное число шагов и часто требует небольших дополнительных модификаций
Метод Нестерова
Для сообществ математической оптимизации и машинного обучения фамилия «Нестеров» уже давно стало нарицательной. В 80х годах прошлого века Ю.Е. Нестеров придумал интересный вариант инерционного метода, который имеет вид
при этом не предполагается какого-то сложного подсчета как в методе сопряженных градиентов, в целом поведение метода похоже на метод тяжелого шарика, но при этом его сходимость обычно гораздо надежнее как в теории, так и на практике.
Стохастический градиентный спуск
Единственное формальное отличие от обычного градиентного спуска — использование вместо градиента функции такой, что ( — математическое ожидание по случайной величине ), таким образом стохастический градиентный спуск имеет вид
— это некоторый случайный параметр, на который мы не влияем, но при этом в среднем мы идем против градиента. В качестве примера рассмотрим функции
Если принимает значения равновероятно, то как раз в среднем — это градиент . Этот пример показателен еще и следующим: сложность вычисления градиента в раз больше, чем сложность вычисления . Это позволяет стохастическому градиентному спуску делать за одно и то же время в раз больше итераций. Несмотря на то, что стохастический градиентный спуск обычно сходится медленней обычного, за счет такого большого увеличения числа итераций получается улучшить скорость сходимости на единицу времени. Насколько мне известно — на данный момент стохастический градиентный спуск является базовым методом обучения большинства нейронных сетей, реализован во всех основных библиотеках по ML: tensorflow, torch, caffe, CNTK, и т.д.
Стоит отметить, что идеи иннерционных методов применяются для стохастического градиентного спуска и на практике часто дают прирост, в теории же обычно считается, что асимптотическая скорость сходимости не меняется из-за того, что основная погрешность в стохастическом градиентном спуске обусловлена дисперсией .
Субградиентный спуск
Эта вариация позволяет работать с недифференцируемыми функциями, её я опишу более подробно. Придется опять вспомнить линейное приближение — дело в том, что есть простая характеристика выпуклости через градиент, дифференцируемая функция выпукла тогда и только тогда, когда выполняется для всех . Оказывается, что выпуклая функция не обязаны быть дифференцируемой, но для любой точки обязательно найдется такой вектор , что для всех . Такой вектор принято называть субградиентом в точке , множество всех субградиентов в точки называют субдифференциалом и обозначают (несмотря на обозначение — не имеет ничего общего с частными производными). В одномерном случае — это число, а вышеуказанное свойство просто означает, что график лежит выше прямой, проходящей через и имеющей тангенс угла наклона (смотрите рисунки ниже). Отмечу, что субградиентов для одной точки может быть несколько, даже бесконечное число.


Вычислить хотя бы один субградиент для точки обычно не очень сложно, субградиентный спуск по сути использует субградиент вместо градиента. Оказывается — этого достаточно, в теории скорость сходимости при этом падает, однако например в нейронных сетях недифференцируемую функцию любят использовать как раз из-за того, что с ней обучение проходит быстрее (это кстати пример невыпуклой недифференцируемой функции, в которой успешно применяется (суб)градиентный спуск. Сама по себе функция выпукла, но многослойная нейронная сеть, содержащая , невыпукла и недифференцируема). В качестве примера, для функции субдифференциал вычисляется очень просто
Пожалуй, последняя важная вещь, которую стоит знать, — это то, что субградиентный спуск не сходится при постоянном размере шага. Это проще всего увидеть для указанной выше функции . Даже отсутствие производной в одной точке ломает сходимость:
- Допустим мы начали из точки .
- Шаг субградиентного спуска:
Где обычно или . На практике я часто видел успешное применение шагов , хоть и для таких шагов вообще говоря не будет сходимости.
Proximal методы
К сожалению я не знаю хорошего перевода для «proximal» в контексте оптимизации, поэтому просто так и буду называть этот метод. Proximal-методы появились как обобщение проективных градиентных методов. Идея очень простая: если есть функция , представимая в виде суммы , где — дифференцируемая выпуклая функция, а — выпуклая, для которой существует специальный proximal-оператор (в этой статье ограничусь лишь примерами, описывать в общем виде не буду), то свойства сходимости градиентного спуска для остаются и для градиентного спуска для , если после каждой итерации применять этот proximal-оператор для текущей точки , другими словами общий вид proximal-метода выглядит так:
-
— индикатор-функция выпуклого множества , то есть
В этом случае — это проекция на множество , то есть «ближайшая к точка множества ». Таким образом, мы ограничиваем градиентный спуск только на множество , что позволяет решать задачи с ограничениями. К сожалению, вычисление проекции в общем случае может быть еще более сложной задачей, поэтому обычно такой метод применяется, если ограничения имеют простой вид, например так называемые box-ограничения: по каждой координате
Заключение
На этом заканчиваются основные известные мне вариации градиентного метода. Пожалуй под конец я бы отметил, что все указанные модификации (кроме разве что метода сопряженных градиентов) могут легко взаимодействовать друг с другом. Я специально не стал включать в эту перечень метод Ньютона и квазиньютоновские методы (BFGS и прочие): они хоть и используют градиент, но при этом являются более сложными методами, требуют специфических дополнительных вычислений, которые обычно более вычислительно затратны, нежели вычисление градиента. Тем не менее, если этот текст будет востребован, я с удовольствием сделаю подобный обзор и по ним.
В работе рассматривается задача поиска минимума функции , записываемая в виде:
Пусть функция такова, что можно вычислить ее градиент. Тогда можно применить метод градиентного спуска, описанный в данной статье.
В статье приведены теоремы сходимости метода градиентного спуска, а также рассмотрена его варианты:
- Метод градиентного спуска с постоянным шагом
- Метод градиентного спуска с дроблением шага
- Метод наискорейшего спуска
Метод градиентного спуска

Идея метода
Основная идея метода заключается в том, чтобы осуществлять оптимизацию в направлении наискорейшего спуска, а это направление задаётся антиградиентом :
- постоянной, в этом случае метод может расходиться;
- дробным шагом, т.е. длина шага в процессе спуска делится на некое число;
- наискорейшим спуском:
Алгоритм
Выход: найденная точка оптимума
- Повторять:
- , где выбирается одним из описанных выше способов
- если выполен критерий останова, то возвращаем текущее значение
Критерий останова
Критерии остановки процесса приближенного нахождения минимума могут быть основаны на различных соображениях. Некоторые из них:
Здеcь - значение, полученное после -го шага оптимизации. - наперед заданное положительное число.
Сходимость градиентного спуска с постоянным шагом
Теорема 1 о сходимости метода градиентного спуска спуска с постоянным шагом.
Пусть , функция дифференцируема, ограничена снизу. Пусть выполняется условие Липшица для градиента : . Пусть .
Тогда при любом выборе начального приближения.
В условиях теоремы градиентный метод обеспечивает сходимость либо к точной нижней грани (если функция не имеет минимума) либо к значению Существуют примеры, когда в точке реализуется седло, а не минимум. Тем не менее, на практике методы градиентного спуска обычно обходят седловые точки и находят локальные минимумы целевой функции.
Определение. Дифференцируемая функция называется сильно выпуклой (с константой ), если для любых и из справедливо
Теорема 2 о сходимости метода градиентного спуска спуска с постоянным шагом.
Пусть функция дифференцируема, сильно выпукла с константой . Пусть выполняется условие Липшица для градиента : . Пусть .
Тогда при любом выборе начального приближения.
Выбор оптимального шага

Константа , фигурирующая в теореме 2 и характеризующая скорость сходимости метода, зависит от шага . Нетрудно видеть, что величина минимальна, если шаг выбирается из условия , т. е. если .
При таком выборе шага оценка сходимости будет наилучшей и будет характеризоваться величиной:
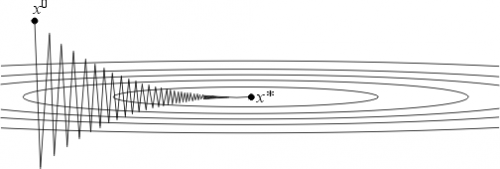
В качестве и могут выступать равномерные по x оценки сверху и снизу собственных значений оператора . Если , то и метод сходится очень медленно. Геометрически случай соответствует функциям с сильно вытянутыми линиями уровня (см. рис. 2). Простейшим примером такой функции может служить функция на , задаваемая формулой:
Поведение итераций градиентного метода для этой функции изображено на рис. 2 — они, быстро спустившись на "дно оврага", затем медленно "зигзагообразно" приближаются к точке минимума. Число (характеризующее, грубо говоря, разброс собственных значений оператора ) называют числом обусловленности функции . Если , то функции называют плохо обусловленными или овражными. Для таких функций градиентный метод сходится медленно.
Но даже для хорошо обусловленных функций проблема выбора шага нетривиальна в силу отсутствия априорной информации о минимизируемой функции. Если шаг выбирается малым (чтобы гарантировать сходимость), то метод сходится медленно. Увеличение же шага (с целью ускорения сходимости) может привести к расходимости метода. Далее будут описаны два алгоритма автоматического выбора шага, позволяющие частично обойти указанные трудности.
Градиентный метод с дроблением шага
В этом варианте градиентного метода величина шага на каждой итерации выбирается из условия выполнения неравенства
где - некоторая заранее выбранная константа.
Процедуру нахождения такого обычно оформляют так. Выбирается число и некоторый начальный шаг . Теперь для каждого k полагают и делают шаг градиентного метода. Если с таким условие (2) выполняется, то переходят к следующему k. Если же (2) не выполняется, то умножают на ("дробят шаг") и повторяют эту процедуру до тех пор пока неравенство (2) не будет выполняться. В условиях теоремы 1 эта процедура для каждого k за конечное число шагов приводит к нужному .
Можно показать, что в условиях теоремы 2 градиентный метод с дроблением шага линейно сходится. Описанный алгоритм избавляет нас от проблемы выбора на каждом шаге, заменяя ее на проблему выбора параметров и , к которым градиентный метод менее чувствителен. При этом, разумеется, объем вычислений возрастает (в связи с необходимостью процедуры дробления шага), впрочем, не очень сильно, поскольку в большинстве задач основные вычислительные затраты ложатся на вычисление градиента.
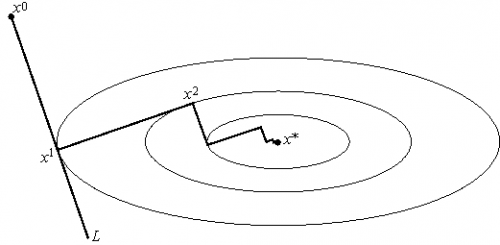
Метод наискорейшего спуска

Этот вариант градиентного метода основывается на выборе шага из следующего соображения. Из точки будем двигаться в направлении антиградиента до тех пор пока не достигнем минимума функции f на этом направлении, т. е. на луче :
Другими словами, выбирается так, чтобы следующая итерация была точкой минимума функции f на луче L (см. рис. 3). Такой вариант градиентного метода называется методом наискорейшего спуска. Заметим, кстати, что в этом методе направления соседних шагов ортогональны.
Метод наискорейшего спуска требует решения на каждом шаге задачи одномерной оптимизации. Практика показывает, что этот метод часто требует меньшего числа операций, чем градиентный метод с постоянным шагом.
В общей ситуации, тем не менее, теоретическая скорость сходимости метода наискорейшего спуска не выше скорости сходимости градиентного метода с постоянным (оптимальным) шагом.
Числовые примеры
Метод градиентного спуска с постоянным шагом
Для исследования сходимости метода градиентного спуска с постоянным шагом была выбрана функция:
Начальное приближение - точка (10,10). Использован критерий останова:
Результаты эксперимента отражены в таблице:
| Значение шага | Достигнутая точность | Количество итераций |
|---|---|---|
| 0.1 | метод расходится | |
| 0.01 | 2e-4 | 320 |
| 0.001 | 2e-3 | 2648 |
| 0.0001 | 1e-2 | 20734 |
Из полученных результатов можно сделать вывод, что при слишком большом чаге метод расходится, при слишком малом сходится медленно и точчность хуже. Надо выбирать шаг наибольшим из тех, при которых метод сходится.
Градиентный метод с дроблением шага
Для исследования сходимости метода градиентного спуска с дроблением шага (2) была выбрана функция:
Начальное приближение - точка (10,10). Использован критерий останова:
Результаты эксперимента отражены в таблице:
| Значение параметра | Значение параметра | Значение параметра | Достигнутая точность | Количество итераций |
|---|---|---|---|---|
| 0.95 | 0.95 | 1 | 5e-4 | 629 |
| 0.1 | 0.95 | 1 | 1e-5 | 41 |
| 0.1 | 0.1 | 1 | 2e-4 | 320 |
| 0.1 | 0.95 | 0.01 | 2e-4 | 320 |
Из полученных результатов можно сделать вывод об оптимальном выборе параметров: , хотя метод не сильно чувствителен к выбору параметров.
Метод наискорейшего спуска
Для исследования сходимости метода наискорейшего спуска была выбрана функция:
Начальное приближение - точка (10,10). Использован критерий останова:
Для решения одномерных задач оптимизации использован метод золотого сечения.
Метод получил точность 6e-8 за 9 итераций.
Отсюда можно сделать вывод, что метод наискорейшего спуска сходится быстрее, чем градиентный метод с дроблением шага и метод градиентного спуска с постоянным шагом.
Недостатком методом наискорейшего спуска явлляется необходимость решать одномерную задачу оптимизации.
Рекомендации программисту
При программировании методов градиентного спуска следует аккуратно относится к выбору параметров, а именно
- Метод градиентного спуска с постоянным шагом: шаг следует выбирать меньше 0.01, иначе метод расходится (метод может расходится и при таком шаге в зависимости от исследуемой функции).
- Градиентный метод с дроблением шага не очень чувствителен к выбору параметров. Один из вариантов выбора параметров:
- Метод наискорейшего спуска: в качестве метода одномерной оптимизации можно использовать метод золотого сечения (когда он применим).
Заключение
Методы градиентного спуска являются достаточно мощным инструментом решения задач оптимизации. Главным недостатком методов является ограниченная область применимости.
Читайте также: