Мебельная фабрика выпускает столы стулья бюро и книжные шкафы решение в excel
Обновлено: 04.07.2024
Одним из способов решения экономических задач с помощью матриц является метод, основанный на использовании формулы Крамера . Этот способ позволяет с минимальными затратами труда и времени обрабатывать разнообразный статистический материал. В данной работе студентом составлены производственные задачи и приведено их решение.
| Вложение | Размер |
|---|---|
| 4_granko_da.ppt | 958 КБ |
Предварительный просмотр:
Подписи к слайдам:
КРАЕВОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «АЧИНСКИЙ КОЛЛЕДЖ ОТРАСЛЕВЫХ ТЕХНОЛОГИЙ И БИЗНЕСА» (КГБПОУ «АЧИНСКИЙ КОЛЛЕДЖ ОТРАСЛЕВЫХ ТЕХНОЛОГИЙ И БИЗНЕСА» Решение задач в экономике методом Крамера Номинация: 4. Использование математических методов для решения профессионально ориентированных задач. Студент: Гранько Дмитрий Александрович 2 курс Руководитель: Янченко Нина Александровна
Одним из способов решения экономических задач с помощью матриц является метод, основанный на использовании формулы Крамера. Этот способ позволяет с минимальными затратами труда и времени обрабатывать разнообразный статистический материал.
a ₁₁ x ₁ + a ₁₂ x ₂ = b ₁ ; a ₂₁ x ₁ + a ₂₂ x ₂ = b ₂ , ( a ₁₁ a ₂₂ - a ₂₁ a ₁₂ ) x ₁ = b ₁ a ₂₂ - b ₂ a ₁₂ , ( a ₁₁ a ₂₂ - a ₂₁ a ₁₂ ) x ₂ = a ₁₁ b ₂ - a ₂₁ b ₂ .
∆ = a ₁₁ a ₂₂ - a ₁₂ a ₂₁ = . ∆ ₁ = b ₁₁ a ₂₂ - b ₂ a ₁₂ = , ∆ ₂ = a ₁₁ b ₂ - a ₂₁ b ₁ = ∆ ∙ x ₁ = ∆₁; ∆ ∙ x ₂ = ∆₂. Если ∆ ≠ 0, то x ₁ = ∆₁/∆, x ₂ = ∆₂/∆.
Если ∆ = 0, а ∆₁ ≠ 0 (или ∆₂ ≠ 0), то система несовместная. 0 ∙ x ₁ = ∆₁; 0 ∙ x ₂ = ∆₂. Если ∆ = ∆₁ = ∆₂ = 0, то система неопределенная и имеет бесконечное множество решений. 0 ∙ x ₁ = 0; 0 ∙ x ₂ = 0. Пусть ∆ - определитель матрицы системы A , а ∆ȷ - определитель матрицы, получаемой из матрицы А заменой j -го столбца столбцом свободных членов. Тогда, если ∆ ≠ 0, то система имеет единственное решение, определяемое по формуле: X ȷ = ∆ȷ / ∆ ( j = 1,2,…, n ) Эта формула получила название формулы Крамера.
Задача 1: Мебельная фабрика выпускает изделия трех видов: стулья, столы и шкафы. Для их производства используются материалы трех типов: ЛДСП 2500х1830х25мм, МДФ 2800*2070*6 мм, ДВПО 2745*1220*3,2. Нормы расхода каждого из них на одно изделие и объем расхода материалов на один день заданы таблицей: Найти ежедневный объем выпуска каждого вида изделий.
Решение: Пусть ежедневно фабрика выпускает x ₁ стульев, x ₂ столов и x ₃ шкафов. Тогда в соответствии с расходом материалов каждого вида имеем систему: 0,9 x ₁ + 1,8 x ₂ + 5,7 x ₃ = 1560 0,75 x ₁ + 1,3 x ₂ + 4,5 x ₃ = 1195 0,4 x ₁ + 2 x ₂ + 3,5 x ₃ = 1270 ∆ = 0,096 ∆₁ = 28,8 ∆₂ = 38,4 ∆₃ = 9,6 x ₁ = 28,8/0,096 = 300 x ₂ = 38,4/0,096 = 400 x ₃ = 9,6/0,096 = 100 Ответ: фабрика выпускает ежедневно 300 стульев, 400 столов, 100 шкафов.
Задача 2: Типография производит печать продукции трех видов: газеты, журналы, книги. Для их производства используется сырье трех типов: бумага 297×420 мм, краска для печати 1 л., бумвинил 1 м². Нормы расхода каждого из них на одну продукцию и объем расхода сырья на один день заданы таблицей: Найти ежедневный объем выпуска каждого вида продукции.
Решение: Пусть ежедневно типография выпускает x ₁ газет, x ₂ журналов и x ₃ книг. Тогда в соответствии с расходом материалов каждого вида имеем систему: 5 x ₁ + 25 x ₂ + 150 x ₃ = 23750 1,3 x ₁ + 2,1 x ₂ + 5,4 x ₃ = 1715 1,2 x ₃ = 120 ∆ = -26,4 ∆₁ = -13200 ∆₂ = -6600 ∆₃ = -2640 x ₁ = -13200/(-26,4) = 500 x ₂ = -6600/(-26,4) = 250 x ₃ = -2640/(-26,4) = 100 Ответ: типография выпускает ежедневно 500 газет, 250 журналов и 100 книг
Задача 3: Кондитерская фабрика производит продукцию трех видов: торты, пирожные и рулеты. Для их производства используется сырье трех типов: мука 1 кг, молоко 1 л., сахар 1 кг. Нормы расхода каждого из них на одну продукцию и объем расхода сырья на один день заданы таблицей: Найти ежедневный объем выпуска каждого вида продукции.
Решение: Пусть ежедневно фабрика выпускает x ₁ тортов, x ₂ пирожных и x ₃ рулетов. Тогда в соответствии с расходом сырья каждого вида имеем систему: 1,6 x ₁ + 0,3 x ₂ + 0,8 x ₃ = 216 2,7 x ₁ + 0,2 x ₂ + 0,6 x ₃ = 232 0,6 x ₁ + 0,1 x ₂ + 0,4 x ₃ = 88 ∆ = -0,064 ∆₁ = -3,2 ∆₂ = -12,8 ∆₃ = -6,08 x ₁ = -3,2/-0,064= 50 x ₂ = -12,8/-0,064 = 200 x ₃ = -6,08/-0,064 = 95 Ответ: фабрика выпускает ежедневно 50 тортов, 200 пирожных и 95 рулетов.
Задача 4: Автомобильный завод производит продукцию трех видов: легковые автомобили, грузовые автомобили, автобусы. Для их производства используются материалы трех типов: оцинкованная сталь 1250*2500*0,65 мм, листовой алюминий 1,5*1500*3000 мм, чугун. Нормы расхода каждого из них на одну продукцию и объем расхода сырья на один день заданы таблицей: Найти ежедневный объем выпуска каждого вида продукции.
Решение: Пусть ежедневно завод выпускает x ₁ легковых автомобилей, x ₂ грузовых автомобилей и x ₃ автобусов. Тогда в соответствии с расходом сырья каждого вида имеем систему: 235 x ₁ + 280 x ₂ + 285 x ₃ = 5780 135 x ₁ + 240 x ₂ + 255 x ₃ = 3990 105 x ₁ + 175 x ₂ + 185 x ₃ = 3005 ∆ = 2250 ∆₁ = 33750 ∆₂ = 11250 ∆₃ = 6750 x ₁ = 33750/2250 = 15 x ₂ = 11250/2250 = 5 x ₃ = 6750/2250 = 3 Ответ: фабрика выпускает 15 легковых автомобилей, 5 грузовых автомобилей и 3 автобуса.
Задача 5: Швейная фабрика производит продукцию трех видов: рубашки, брюки, юбки. Для их производства используются материалы трех типов: хлопковая ткань 1200х680 мм, сатин 1300х680 мм, нити швейные 200 м. Нормы расхода каждого из них на одну продукцию и объем расхода сырья на один день заданы таблицей: Найти ежедневный объем выпуска каждого вида продукции.
Решение: Пусть ежедневно завод выпускает x ₁ рубашек, x ₂ брюк и x ₃ юбок. Тогда в соответствии с расходом сырья каждого вида имеем систему: 6,2 x ₁ + 6,3 x ₂ + 5,2 x ₃ = 2399 6,1 x ₂ + 5 x ₃ = 1418 0,7 x ₁ + 1,3 x ₂ + 0,9 x ₃ = 386,5 ∆ = -6,416 ∆₁ = -962,4 ∆₂ = -834,08 ∆₃ = -802 x ₁ = -962,4/-6,416 = 150 x ₂ = -834,08/-6,416 = 130 x ₃ = -802/-6,416 = 125 Ответ: фабрика выпускает 150 рубашек, 130 брюк и 125 юбок.
Литература Основы высшей математики: Учеб. пособие для вузов/В.С. Шипачев; под ред.акад. А.Н. Тихонова. —5-е изд.,стер. — М. Высш. Шк., 2003. — 279с. Высшая математика для экономистов: учебное пособие для студентов экономических специальностей высших учебных заведений /Н.Ш Кремер, Б.А. Путко. — М.: Банки и биржи ЮНИТИ, 1997. – 239с. Математика. Задачник : учеб. Пособие для образоват. Учреждений нач. и сред. Проф. образования / М.И. Башмаков. — 3-е изд., стер. — М.: Издательский центр «Акадения», 2013. —416с.
Пусть предприятие (например, мебельная фабрика) производит столы и стулья. Расход ресурсов на их производство и прибыль от их реализации представлены ниже:
Расход древесины на изделие, м3
Прибыль от реализации
единицы изделия, руб.
Кроме того, на производство 80 столов заключен контракт с муниципалитетом, который, безусловно, должен быть выполнен. Необходимо найти такую оптимальную производственную программу, чтобы прибыль от реализации продукции была максимальной.
Пусть x1 – количество столов;
х2 – количество стульев.
Тогда система ограничений и целевая функция запишутся следующим образом:
x180 (контракт с муниципалитетом);
x1 0; х2 0;
x1, х2 – целые числа.
Для решения задачи в Excel запишем ее виде, представленном на рис. 3.4.

Рис. 3.4. Запись исходных данных для решения задачи линейной оптимизации
Для решения задачи вызовем меню Сервис-Поиск решения (Tools-Solver).
В открывшемся диалоговом окне Поиск решения (рис. 3.5.) укажем:
адрес целевой ячейки (в нашем примере D5);
диапазон искомых ячеек (А2:A3);
Добавления, изменения и удаления ограничений производятся с помощью кнопок Добавить, Изменить, Удалить (Add, Change, Delete).
Для нахождения оптимального решения нажмем кнопку Выполнить (Solve). В результате в таблице получим значение целевой функции – 42400 млн руб. при x1 = 80 и x2 = 1400.
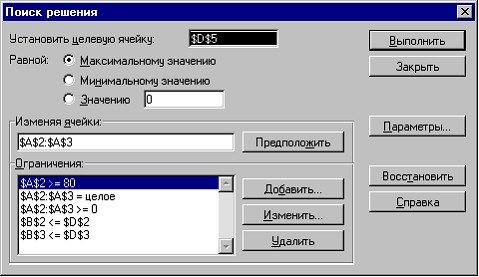
Рис. 3.5. Диалоговое окно Поиск решения
Диалоговое окно Результаты поиска решения позволяет (рис. 3.6.):
сохранить на текущем рабочем листе найденное оптимальное решение; восстановить первоначальные значения; сохранить сценарий; выдать отчеты по результатам, устойчивости, пределам, необходимые для анализа найденного решения.
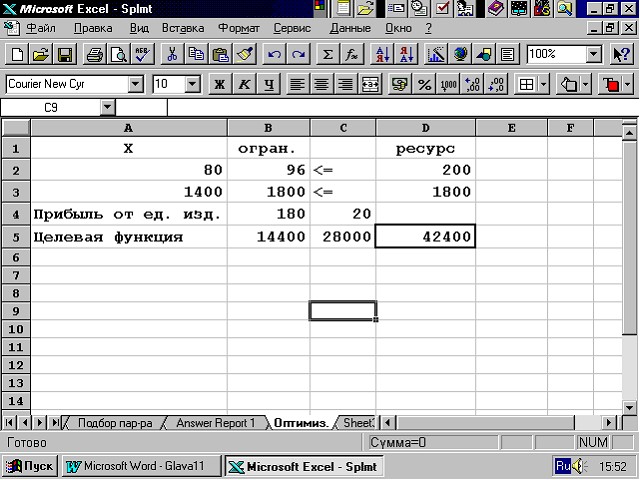
Рис.3.6. Рабочий лист с найденным оптимальным решением
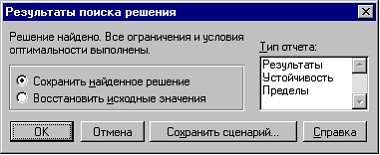
Рис. 3.7. Диалоговое окно Результаты поиска решения
Если щелкнуть по кнопке ОК, то на месте исходной таблицы получим таблицу с найденными оптимальными значениями (см. рис. 3.7).
Как видно из результатов решения, предприятию производить столы не очень выгодно. Поэтому оно ограничило объем их выпуска в количестве, необходимом для выполнения контракта. Остальные ресурсы направлены на производство стульев.
Мебельная фабрика выпускает столы, стулья, платяные и книжные шкафы. При изготовлении этой продукции используется два типа древесных материалов (досок). В таблице приведены нормативные затраты на единицу изделия. Объемы наличных ресурсов каждого типа соответственно равны 1500, 1000, 3200. Прибыль от реализации единицы изделия - 60, 25, 140 и 160 р. соответственно.
Существуют следующие условия: столов необходимо произвести не менее 40, стульев - не менее 120, платяных шкафов - не менее 20, книжных шкафов - не более 20. Определить ассортимент продукции, максимизирующей прибыль фабрики в данных условиях. Запас какого типа досок следует изменить в первую очередь и на сколько для увеличения прибыли.
Операция - обеспечение наибольшей прибыли от реализации выпускаемой продукции мебельной фабрики, при заданных условиях.
В качестве параметров, описывающих количество каждого вида продукции, примем:
Руководство мебельной фабрики, как постановщик задачи. Непосредственный изготовитель продукции (трудовой ресурс) - лица, изготовляющие мебель. Покупатель (или заказчик) - лицо, обеспечивающее существование имеющейся цели. Поставщик материала (используемого ограниченного ресурса) - лицо, принимающее участие в процессе достижения цели.
Лицо, принимающее решение (ЛПР) - индивид или группа людей, которые осуществляют выбор и несут ответственность за принятое решение в соответствии со своими полномочиями, установленными руководством фирмы.
Исследователь операций - лицо, чья работа состоит в рациональной организации процесса, поиска и разработки методов решений поставленной задачи. В данной задаче исследование операций осуществляю я.
Существуют ограничения на количество ресурсов и выпускаемых изделий:
Доски I типа, доски II типа, трудовой ресурс, установленное условие количества изделий. Данные ограничения приведены в системе:
Цель задачи: Определить, какое количество изделий, выпускаемых фабрикой, удовлетворяющих последней системе, будет максимизировать прибыль.
Стратегиями оперирующей стороны в данной операции называются допустимые способы расходования ею имеющихся активных средств. В виду поставленной цели и имеющихся у меня в настоящий момент знаний, лучшая и выполнимая стратегия - рассчет оптимального количества изделий. ЛПР может перейти к другим стратегиям, путем введения новых ограничений, и активных средств. Так же можно предположить существование субъективных желаний исполнителя и заказчика, определяющее выбор стратегии ОС. Количество этих стратегий определяется многоугольником решений задачи. ЛПР может принять и выбрать любую из них.
Задача стохастического программирования . . . . . . . . . . . . . . . . . . .
2 Решение задачи оценки показателей эффективности стохастической сети
с использованием методики GERT. Выбор и использование математиче-
ского пакета Matlab для решения сформулированной задачи.
2.1 Постановка задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
2.2 Ход работы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
2.3 Результат . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
3 Поиск оптимальной стратегии принятия решений с использованием мар-
3.1 Постановка задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
3.2 Марковская модель принятия решений . . . . . . . . . . . . . . . . . . . . . . 25
3.3 Метод итерации по стратегиям . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
3.4 Метод линейного программирования . . . . . . . . . . . . . . . . . . . . . . . 28
4 Поиск оптимальных параметров сети систем массового обслуживания. 32
4.1 Постановка задачи . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
4.2 Алгоритм решения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
4.3 Решение по алгоритму . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
4.4 Решение дискретным линейным методом программирования . . . . . . . . . 38
Список используемой литературы
1 Варианты формализации многокритериальной задачи и их решение с использованием Optimization Toolbox системы Matlab.
1.1 Постановка задачи
Мебельная фабрика выпускает столы, стулья, бюро и книжные шкафы. При изготовлении используются два типа досок, причем фабрика имеет в наличии 1500 м досок первого типа и 1000 м досок второго типа. Кроме того, заданы трудовые ресурсы в количестве 800 чел/час. В таблице приводятся нормативы затрат каждого из видов ресурсов на изготовление 1 ед изделия и прибыль от реализации 1 ед изделия.
Затраты на 1 ед изделия
Доски первого типа, м
Доски второго типа, м
Трудовые ресурсы, чел/час
Таблица 1: Нормативы затрат ресурсов на единицу изделия
По этим исходным данным решить задачу определения оптимальный ассортимент, максимизирующий прибыль (разность между выручкой и расходами.) и выручку при следующих ценах изготавливаемую мебель:
∙ книжный шкаф – 80 руб.
В отчёте необходимо описать:
1. Осуществление перехода от многокритериальной задачи к однокритериальной с использованием различных подходов.
2. Решение задачи стохастического программирования для одной из однокритериаль-
ных задач, превратив детерминированное ограничение в вероятностное по схеме:
Менять в следующем диапазоне 0.1 ≤ ≤ 0.9.
Считать случайной величиной или элементы < >-й строки матрицы < >(по выбору).
1.2 Выделение главного критерия
Выбирается один из критериев, например , который наиболее полно отражает цель принятия решений. Остальные критерии учитываются только с точки зрения возможного указания их нижних границ ( ) ≥ , ̸= . Таким образом, исходная задача многокритериального принятия решений заменяется однокритериальной задачей с критерием , т.е.
Для производства столов и шкафов мебельная фабрика использует необходимые ресурсы. Нормы затрат ресурсов на одно изделие данного вида, прибыль от реализации одного изделия и общее количество имеющихся ресурсов каждого вида приведены в табл. 8.1.
| Ресурсы | Нормы затрат ресурсов на одно изделие | Общее количество ресурсов | |
| стол | шкаф | ||
| Древесина 1 вида | 0,2 | 0,1 | |
| Древесина 2 вида | 0,1 | 0,3 | |
| Трудоемкость (человеко-часов) | 1,2 | 1,5 | 371,4 |
| Прибыль от реализации одного изделия (руб.) |
Определить, сколько столов и шкафов фабрике следует изготовлять, чтобы прибыль от их реализации была максимальной.
Для решения этой задачи необходимо построить математическую модель. Процесс построения модели можно начать с ответа на следующие три вопроса:
1. Для определения каких величин строится модель?
2. В чем состоит цель, для достижения которой из множества всех допустимых значений переменных выбираются оптимальные?
3. Каким ограничениям должны удовлетворять неизвестные?
В данном случае мебельной фабрике необходимо спланировать объем производства столов и шкафов так, чтобы максимизировать прибыль. Поэтому переменными являются: х1 - количество столов, х2 - количество шкафов
Суммарная прибыль от производства столов и шкафов равна z=6*x1+8*x2. Целью фабрики является определение среди всех допустимых значений х1 и х2 таких, которые максимизируют суммарную прибыль, т.е. целевую функцию z
Ограничения, которые налагаются на х1 и х2:
· объем производства шкафов и столов не может быть отрицательным, следовательно: х1, х2 ³ 0.
· нормы затрат древесины на столы и шкафы не может превосходить максимально возможный запас данного исходного продукта, следовательно:
Кроме того, ограничение на трудоемкость не превышает количества затрачиваемых ресурсов
Таким образом, математическая модель данной задачи имеет следующий вид:
при следующих ограничениях:
1,2x1+ 1,5х2 £ 371,4
Данная модель является линейной, т.к. целевая функция и ограничения линейно зависят от переменных.
1. Отвести ячейки A3 и ВЗ под значения переменных х1 и х2 (рис. 8.1).
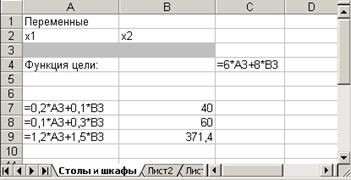
Рис.8.1. Диапазоны, отведенные под переменные,
целевую функцию и ограничения
2. В ячейку С4 ввести функцию цели: =6*АЗ+8*ВЗ, в ячейки А7:А9 ввести левые части ограничений:
а в ячейки В7:В9 - правые части ограничений. (рис.8.1.)
3. Выбрать команды Сервис/Поиск решения (Tools/Solver) и заполнить открывшееся диалоговое окно Поиск решения (Solver) как показано на рис 8.2. Средство поиска решений является одной из надстроек Excel. Если в меню Сервис (Тоо1з) отсутствует команда Поиск решения (Solver), то для ее установки необходимо выполнить команду Сервис/ Надстройки/ Поиск решения (Tools/Add-ins/Solver). Для ввода ограничений нажмите кнопку Добавить.
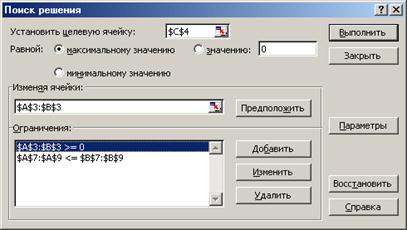
Рис. 8.2. Диалоговое окно Поиск решения задачи о максимизации прибыли на фабрике
Внимание! В диалоговом окне Параметры поиска решения (Solver Options) необходимо установить флажок Линейная модель (Assume Linear Model) (Рис.8.3.).
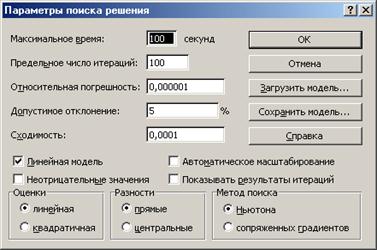
Рис.8.3. Диалоговое окно Параметры поиска решения
4. После нажатия кнопки Выполнить (Solve) открывается окно Результаты поиска решения (Solver Results), которое сообщает, что решение найдено (рис. 8.4).
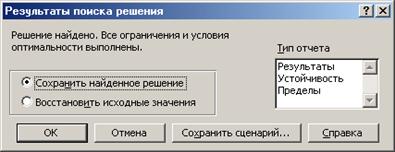
Рис. 8.4. Диалоговое окно Результаты поиска решения
5. Результаты расчета задачи представлены на рис. 8.5, из которого видно, что оптимальным является производство 102 столов и 166 шкафов. Этот объем производства принесет фабрике 1940 руб. прибыли.
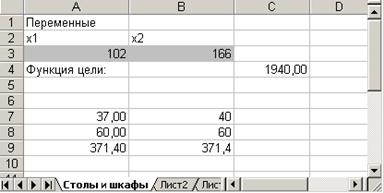
Рис.8.5. Результаты расчета с помощью средства поиска решений для задачи максимизации выпуска столов и шкафов
Индивидуальное задание
1.Построить математическую модель задачи, согласно вашему варианту.
2.Решить задачу с помощью средства MS Excel Поиск решения.
Читайте также:

