Метод идеальной точки excel
Обновлено: 07.07.2024
Данный метод называют также методом смещенного идеала. Метод предполагает построение «идеального объекта», т. е. некоторого варианта решения, которое может приниматься как наилучшее возможное решение. Образ такого «идеального объекта» может не принадлежать реальному множеству объектов и даже не существовать в действительности.
Наличие идеального объекта задает точку отсчета при сравнении реальных альтернатив с этим идеальным вариантом. При этом объекты из множества допустимых альтернатив Аг,А2. Ат> сравниваются с моделью сформированного «идеального объекта» по критерию расстояния от текущего варианта до идеального. На основании этого значения расстояния происходит процедура ранжирования альтернатив по степени близости к «идеальному объекту».
Процедура выбора наиболее предпочтительного объекта состоит из следующих шагов:
- 1) формирование «идеального объекта»;
- 2) определение для каждого объекта многокритериальной метрики (расстояния) до «идеального объекта»;
- 3) анализ множества объектов на соответствие (степень близости) «идеальному объекту»;
- 4) исключение тех объектов из исходного множества г, А2, . Ат>, которые признаны при анализе заведомо нелучшими, и получение сокращенного множества допустимых вариантов;
- 5) оценка сокращенного множества допустимых вариантов на оптимальность решения (нахождение лучшего решения). Если решение выбрано, то процедура выбора заканчивается, если нет, то переход к п. 1 и повторение этапов 1—4 для нового цикла по сокращенному множеству допустимых вариантов.
Пример 8.2. Выбрать лучший дождевальный агрегат методом идеальной точки для условия из примера 8.1.
Сформируем идеальный и наихудший объекты, исходя из экономического смысла частных критериев. Это означает, что параметр «идеального объекта» выбирается как максимальное значение из значений данного параметра всех альтернатив, если частный критерий максимизируется. В случае минимизации частного критерия в качестве параметра «идеального» объекта выбирается минимальное значение в столбце.
Как видно, наивысшую ценность имеют альтернативы 2 и 8. Отрицательные значения ценности не должны приниматься во внимание, ибо нас интересуют только сравнительная только сравнительная ценность альтернатив. Таковыми являются альтернативы 3,7, 9 и 10. Наличие отрицательных значений еще раз показывает условность функции ценности, отсутствие у нее в большинстве случаев реального экономического и технологического смысла.
2.2.3.Метод главного критерия
В методе главного критерия в качестве целевого функционала выбирается один из критериальных выходных параметров, наиболее полно с точки зрения исследователя отражающий цели оптимизаций. Остальные частные критерии оптимальности учитываются с помощью введения необходимых критериальных ограничений, определяющих совместно с прямыми и функциональными ограничениями допустимое множество. Основные трудности такого подхода связаны с проблемой назначения критериальных ограничений. Кроме того, в большом числе случаев всегда есть несколько главных критериев, находящихся в противоречии друг с другом.
Главным критерием является , а для 2-го, 3-го и 4-го критерия допустимыми уровнями будут 5, 5 и 4 соответственно. и нам следует уменьшить, а и увеличить. В данном случае оптимальной альтернативой 3-му и 4-му критериям будет являться 2-я альтернатива. Также по главному критерию оптимальной альтернативой является 2-я. Но по главному критерию оптимальна и 9-ая альтернатива, но она не оптимальна по остальным критериям. Следовательно, 2-я альтернатива являются оптимальной при заданных уровнях значимости и данном главном критерии.
2.2.4.Метод идеальной точки
Особую разновидность количественных методов решения многокритериальных задач представляют те, в которых ценность альтернатив определяется не на основе агрегирования оценок по отдельным критериям (построения функции ценности), а путем определения меры близости решения к некому идеальному (так называемой точке идеала, или идеальной точке). Т.е решение должно обеспечивать наибольшее приближение к множеству одновременно недостижимых целей.
Данный метод используется при различных метриках, функциях расстояния. В общем случае:

(14)

где - желательное значение i- того критерия;
S- характеристика метрики.
При S=2 вычисляется евклидово расстояние:

(15)
При S=1 задача сводится к минимизации суммы модулей относительных с учетом «веса» отклонений:

(16)
При S=∞ имеем равномерную метрику, и задача целевого программирования сводится к минимизации максимального относительного отклонения, т.е.

(17)
Таким образом, с помощью табличного процессора MS Excel введем следующие формулы в ячейку B20:
Далее аналогично формулы вставляем по столбцам, и получим результат решения задачи методом идеальной точки (рис.16).
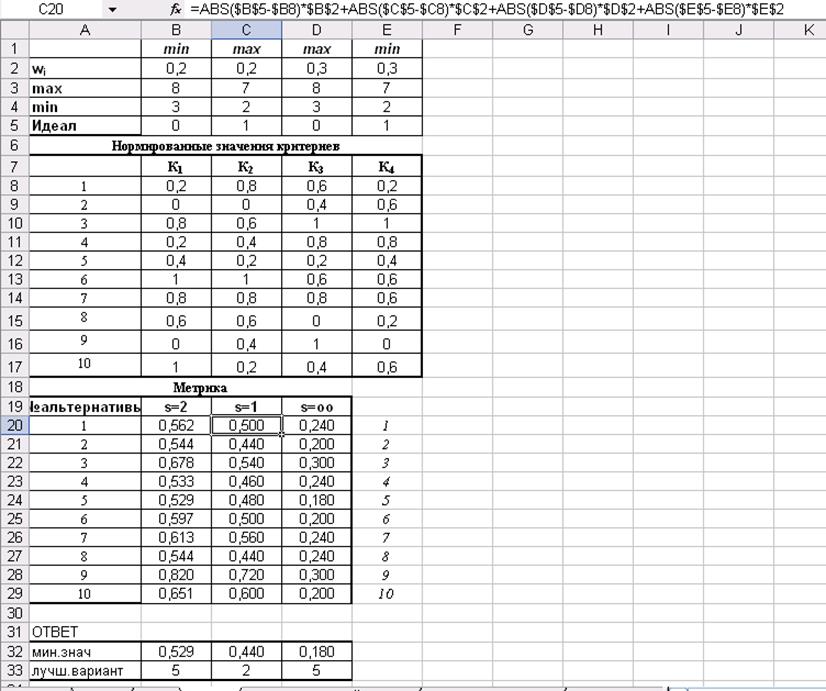
В данном примере лучшим вариантом по двум метрикам является альтернатива 5, по одной метрике альтернатива 2.
В данном примере мы оценивали 10 альтернатив с 4-мя критериями, из них и нам следует уменьшить, а и увеличить, по 4 методам:
· По методу Парето все 10 альтернатив являются оптимальными.
· По методу аддитивной функции ценности наивысшую ценность имеют альтернативы 2 и 8.
· По методу главного критерия 2-я альтернатива являются оптимальной при заданных уровнях значимости и данном главном критерии.
· По методу идеальной точки лучшим вариантом по двум метрикам является альтернатива 5, по одной метрике - альтернатива 2.
Метод идеальной точки
•Идеальной или точкой абсолютного максимума называют точку в
критериальном пространстве, в которой все критерии достигают своих
максимальных значений.
•Если эта точка принадлежит достижимому множеству G, то все
эффективное (паретовское) множество состоит из этой единственной точки
и проблемы как таковой в этом случае нет. Однако идеальная точка обычно
лежит вне множества G и поэтому нереализуема. В связи с этим ее иногда
называют также утопической.
•Идея метода состоит в том, чтобы на множестве G найти точку,
наиболее близкую к идеальной.
2
Решение задачи методом идеальной точки
Задача линейной многокритериальной максимизации с двумя
переменными и двумя целевыми функциями
Пример 1. Найти значения переменных, при которых функции
L1 = 2x1 + x2 + 1 → max
L2 = x1 - x2 + 5 → max
при ограничениях:
x1 + 2x2 ≤ 8,
0 ≤ x ≤ 6,
0 ≤ x ≤ 3.
3
Решение.
1) Построим область допустимых решений. Введем на плоскости прямоугольную
систему координат и построим множество X — область допустимых решений
данной задачи в указанной системе координат. Ограничительные условия
определяют на плоскости многоугольник ABCDE (Рис. 1), вершины которого
имеют соответственно координаты: (0; 0), (0; 3), (2; 3), (6; 1), (6; 0). Следовательно,
представляет собою многоугольник ABCDE.
4
Рисунок 1
2) Строим область допустимых решений в пространстве критериев. Подвергнем
координаты каждой точки плоскости преобразованиям L1 = 2x1+x2+1 → max и L2 = x1-x2+5
→ max . Получим плоскость OL1L2. При этом в силу линейности проводимых
преобразований прямоугольная система координат перейдет в прямоугольную систему
координат , а многоугольник ABCDE в многоугольник A*B*C*D*E*, вершины которого
имеют соответственно координаты: (1; 5), (4; 2), (8; 4), (14; 10), (13; 11) (рис. 2).
Для наглядности укажем описанное соответствие вершин: A(0; 0) → A*(1; 5), B(0; 3)
→ B*(4; 2), C(2; 3) → C*(8; 4), D(6; 1) → D*(14; 10), E(6; 0) → E*(13; 11).
Таким образом, все точки, координаты которых удовлетворяют условиям L 1= 2x1+x2+1
→ max, L2 = x1-x2+5 → max и (x1, x2) ϵ X, определяют на плоскости
многоугольник A*B*C*D*E*. Следовательно, область допустимых решений данной задачи
в системе координат (пространстве критериев) представляет собою
многоугольник A*B*C*D*E*.
5
Рисунок 2
3) Находим множество Парето. Это отрезок D*E*.
4) Находим точку утопии. Выбираем комбинацию наилучших значений всех
критериев. В данном случае это точка U с координатами (14; 11).
6
5) Находим идеальную точку. Теперь необходимо найти во множестве Парето
точку, расположенную ближе всех к точке утопии U. Из рис. 3 видно, что точка I ( I1,
I2 ), являющаяся основанием перпендикуляра, проведенного из точки U (14; 11) к
прямой D*E*, принадлежит отрезку D*E*. Это означает, что точка I — искомая.
Рисунок 3
7
6) Находим координаты идеальной точки. Сейчас необходимо вспомнить аналитическую
геометрию: находим уравнение прямой D*E* и находим точку пересечения перпендикуляра
проходящего через точку утопии U получаем координаты идеальной точки I ( I1, I2 ).
8
Замечание. При нахождении расстояния между точкой утопии и идеальной
точкой, учитывая топологию множества Парето, был применен «геометрический»
метод. В общем случае задача нахождения расстояния между указанными точками
решается как экстремальная. Необходимо найти на множестве Парето точку, такую,
что расстояние между ней и точкой утопии минимально.
9
Заключение
Таким образом, метод может быть использован для построения не
популяционных
алгоритмов
Парето-аппроксимации.
Задачу
Парето-
аппроксимации в этом случае сводят к многократному решению задачи
глобальной оптимизации.
10
Аннотация научной статьи по экономике и бизнесу, автор научной работы — Журавлев Валерий Александрович
В статье рассматриваются применение метода «идеальной точки» и оценка рисков при выборе лучших инновационных и инвестиционных проектов по нескольким критериям.The article discusses the application of «ideal point method» and evaluation of risks when choosing the best investment and innovation projects by multiple criteria.
Похожие темы научных работ по экономике и бизнесу , автор научной работы — Журавлев Валерий Александрович
Оптимизация состояния инновационной активности промышленного предприятия на основе метода «Идеальной точки» Об одном подходе к решению задачи севооборота в многокритериальной постановке Выбор стратегии синхронного развития системы трудовых потоков промышленного регионально-отраслевого комплекса Оценка результативности автоматизированных торговых систем на основе непараметрических методов Разработка модели СППР - для малого предприятия по изготовлению печатных плат i Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.РС! 10.21661/Г-474744 В.А. Журавлев
Применение метода «идеальной точки» и учет рисков при выборе лучших проектов
В статье рассматриваются применение метода «идеальной точки» и оценка рисков при выборе лучших инновационных и инвестиционных проектов по нескольким критериям.
Щ Ключевые слова: выбор лучших проектов, учет рисков, метод «идеальной точки».
Application of the «ideal point» method and account of risks when choosing the best projects
The article discusses the application of «ideal point method» and evaluation of risks when choosing the best investment and innovation projects by multiple criteria.
| Keywords:choosing the best projects, risk, an «ideal point method».
В условиях инновационной экономики на предприятиях ежегодно рассматривается значительное количество проектов. В крупных компаниях таких проектов могут быть десятки и сотни.
Такими проектами являются инновационные проекты по созданию новой продукции, развитию ассортимента и повышению качества продукции, проекты по закупке нового оборудования и внедрению новых технологий, выходу на новые рынки и сегменты и др. Каждый проект характеризует системой показателей, которые определяют эффективность и рискованность проекта. Поэтому важной является задача выбора лучших проектов из рассматриваемых для реализации в плановом периоде, с максимальным уровнем получаемого результата и минимальным уровнем риска. Учет рисков проектов является необходимым в условиях неопределенности будущей рыночной ситуации 1.
Когда рассматривается много проектов, которые характеризуются большим количеством параметров эту задачу надо решать с использованием математических методов и информационных технологий, что позволит
повысить обоснованность и ускорить выбор лучших проектов для их реализации.
Одним из эффективных методов выбора лучших проектов, из рассматриваемых, является метод «идеальной точки». Алгоритм метода «идеальной точки» состоит в следующем:
1. Определяется «идеальная точка», т.е. лучшие параметры, с которыми сравниваются параметры рассматриваемых проектов. Такими идеальными параметрами могут быть лучшие значения параметров у всех рассматриваемых проектов или значения, определяемые экспертами.
2. Поскольку параметры проектов могут быть разными по масштабу, определяются их нормированные значения:
где Н1. _ нормированные значение >го параметра ьго проекта, П1. - значение .-го параметра ьго проекта; П.* - значение .-го параметра «идеальной точки»; i -номер проекта, . - номер параметра.
Таким образом, нормированные значения параметров «идеальной точки» равны единице.
3. Поскольку важность параметров проектов может быть разной, то экспертами определяются коэффициенты важности параметров проектов (Wj). Для определения коэффициентов важности можно использовать, например, 5-ти или 10-ти бальную шкалу. Коэффициенты Wj определяются делением на максимальный балл, как в табл. 1.
4. Определяются «расстояния» между проектами. Расстояния между проектами можно определить по двум формулам:
где R1 (^ к) - расстояние между ьм и к-м проектами, Н1. Нк. - нормированные значение .-го параметра для ь го и к-го проекта, R1*(i) - расстояние от 1-го проекта до идеальной точки, Wj - коэффициент важности .-го параметра, п - количество параметров проектов.
Поскольку нормированные значения параметров «идеальной точки» равны 1,0, то расстояние от проектов до «идеальной точки» определяется по формуле (3).
R, (Lk) = max(Wf \H\- НкЛ).
В этом случае расстояние от проекта до «идеальной точки» определяется по формуле (5):
Имеет место соотношение:
6. Затем проекты ранжируются по возрастанию расстояния до «идеальной точки» R*(i). Лучшим считается проект, у которого расстояние до «идеальной точки» является минимальным.
Пример. Рассмотрим 5 проектов, которые оцениваются по трем параметрам: прибыль, затраты и риск убытка. Требуется выбрать три лучших проекта для реализации. В реальных задачах проектов и параметров может быть намного больше, например, может учитываться риск невыполнения проектов в срок и другие.
Для оценки риска убытка проекта можно использовать формулу относительного риска:
5. Второй формулой определения «расстояния» между проектами является (4):
где РиУб - риск получить убыток при реализации проекта, У1 - возможные варианты убытка, Ру - вероятности убытка, П1 - варианты прибыли, Р - вероятности прибыли по возможным результатам проекта.
Уровни риска РиУб убытка проекта оцениваются по таблице 3.
Если риск убытка недопустимый, то проект отклоняется. Дополнительной оценкой риска является оценка колеблемости возможных результатов проекта с помощью коэффициента вариации.
Затем определятся «идеальная точка» как максимальное значение прибыли и минимальные значения затрат и риска по всем проектам, табл. 4.
Нормируем параметры проектов, делением на параметры идеальной точки. Определим коэффициенты важности W: для прибыли - очень важный (1,0), для затрат - менее важный (0,6), для рисков - важный (0,8).
Определение важности параметров проектов
Важность параметра Очень важный Важный Менее важный Маловажный Неважный
Оценки прибыли и убытка проекта
Значения У1 У2 Ук П1 П2 Пт
Вероятность РУ1 РУ2 РУк РП1 РП2 РПт
Уровни риска убытка проекта
РиУб <0,1 0,1-0,3 0,3-0,5 0,5-0,7 0,7-1,0 >1
Уровень риска Минимальный Ниже среднего Средний Выше среднего Критический Недопустимый
Исходные параметры проектов
Параметры Проекты Идеальная точка
Прибыль 40 50 85 80 90 90
Затраты 300 250 300 350 300 250
Риск 0,3 0,4 0,5 0,3 0,7 0,3
Нормированные параметры проектов
Параметры Коэфф. важности параметра Проекты Идеальная точка
Прибыль 1,0 0,44 0,56 0,94 0,89 1,00 1,0
Затраты 0,6 1,20 1,00 1,20 1,40 1,20 1,0
Риск 0,8 1,00 1,33 1,67 1,00 2,33 1,0
Расстояния и ранги проектов до «идеальной точки» по формуле (3)
Проекты 1 2 3 4 5
Расстояние до идеальной точки по формуле (3) 0,568 0,518 0,549 0,264 1,073
Ранг проекта 4 2 3 1 5
Таблица 7 Расстояния и ранги проектов до «идеальной точки» по формуле (5)
Проекты 1 2 3 4 5
Расстояние до идеальной точки по формуле (5) 0,56 0,44 0,53 0,24 1,07
Ранг проекта 4 2 3 1 5
Определим расстояния проектов до «идеальной точки» по формуле (3) и проранжируем проекты по возрастанию расстояния.
По формуле (3) тремя лучшими проектами являются 4-й, 2-й и 3-й проекты с расстояниями до «идеальной точки» 0,264; 0,518; 0,549 соответственно.
Определим расстояния и ранги проектов до «идеальной точки» по формуле (5).
В примере расстояния от проектов до идеальной точки, определенные по формулам (3) и (5) разные, но ранги проектов совпадают. Если ранги некоторых проектов будут не совпадать, то для получения однозначных рангов проектов надо взять средние арифметические рангов для расстояний (3) и (5). Кроме этого, ранги могут корректироваться экспертами с учетом дополнительных критериев.
2. Мазур И.И. Управление проектами: Учеб. пособие для студентов / И.И. Мазур, В.Д. Шапиро, Н.Г. Ольдерог-ге. - 5-е изд., стер. - М.: Омега-Л, 2007. - 664 с.
3. Михайлова Е.Л. Особенности управления риском в условиях капитализации экономики / Е.Л. Михайлова, Л.П. Милешко // Проблемы современной экономики. - 2018. - №1 (65). - С. 51-54.
4. Колесникова Е.В. Особенности управления рисками на микроуровне в реальном секторе экономики / Е.В. Колесникова, О.А. Юшков // Baikal Research Journal. - 2017. - Т. 8. - №2. - С. 30.
5. Волкова О.Н. Управление рисками - оперативный метод формирования промышленной и торговой политики на предприятиях // Инновационные аспекты социально-экономического развития региона: Сборник статей по материалам участников VII Ежегодной научной конференции аспирантов «МГОТУ». - 2017. - С. 181-188.
Чтобы получить более полную характеристику достоинств и недостатков проектируемого объекта, нужно ввести больше критериев качества в рассмотрение. Как результат, задачи проектирования сложных систем всегда многокритериальные, так как при выборе наилучшего варианта приходится учитывать много различных требований, предъявленных к системе [28].
С привычной точки зрения задача со многими критериями решения не имеет, но к счастью это не так, всегда есть возможность одновременного удовлетворения всех заданных условий [51]. А так, как практически любая подобная ситуация допускает разные компромиссные разрешения, то и подходы к их поиску многочисленны и весьма разнообразны.
Перечислим некоторые из подходов к решению задач многокритериальной оптимизации:
1. Метод уступок – лицо, принимающее решения подводится к выбору решения путем постепенного ослабления первоначальных требований, как правило, одновременно невыполнимых.
2. Метод идеальной точки – в области допустимых значений неизвестных ищется такая их совокупность, которая способна обеспечить набор значений критериев, в том или ином смысле ближайший к наилучшему варианту.
3. Метод свертывая – лицо, принимающее решения сводит многокритериальную задачу к задаче с одним критерием.
Ниже, рассмотрим подробно этих методов решения задачи многокритериальной оптимизации [33,46,48,51].
2.1. Метод последовательных уступок
Метод последовательных уступок решения многокритериальных задач применяется в случае, когда частные критерии могут быть упорядочены в порядке убывающей важности [51]. Предположим, что все критерии максимизируются и пронумерованы в порядке убывания их важности. Вначале определяется максимальное значение , первого по важности критерия в области допустимых решений, решив задачу
Затем назначается, исходя из практических соображений и принятой точности, величина допустимого отклонения (экономически оправданной уступки) критерияи отыскивается максимальное значение второго критерияпри условии, что значение первого должно отклоняться от максимального не более чем на величину допустимой уступки, т.е. решается задача



Снова назначается величина уступки по второму критерию, которая вместе с первой используется при нахождении условного экстремума третьего частного критерия и т.д. Наконец, выявляется экстремальное значение последнего по важности критерияпри условии, что значение каждого из первыхчастных критериев отличается от экстремального не более чем на величину допустимой уступки. Получаемое на последнем этапе решение считается оптимальным.
Существенным недостатком метода последовательных уступок является то, что решение, полученное этим методом, может оказаться неоптимальным по Парето [37].
Рассмотрим пример, математическая модель трехкритериальной задачи имеет вид [51]:



Уступка по первому критерию , а по второму.

Открываем электронную книгу Excel и, как и для решения однокритериальной задачи определяем ячейки под переменные . Для этого в ячейку А2 вводим подпись «Переменные», а соседние три ячейки В2, С2 и D2 вводим значения переменных. Это могут быть произвольные числа, например единицы или нули, далее они будут оптимизироваться.
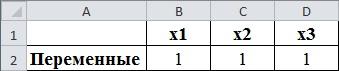
рис. 2.1. Определение переменных значений
В третьей строке задаем целевые функции. В А3 вводим подпись «Целевые», а в В3 формулой «=2*B2+C2-3*D2» задаем первую целевую функцию . Аналогично в С3 и D3 вводим вторуюи третьюцелевую функцию, вводя в С3 «=B2+3*C2-2*D2», а в D3 «=-B2+2*C2+4*D2».
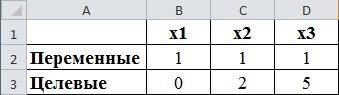
рис.2.2. Определение целевых значений
Ячейка А5 будем называть «Ограничения».

Левые части ограничений распишем от B5:D7, правые части записываем в диапазонF5:F7. Вводим в Е5 формулу «=B5*$B$2+C5*$C$2+D5*$D$2», номера столбцов и номера строк ряда переменных зафиксировано, далее воспользуемся автозаполнением, чтобы заполнить ячейки Е6 и Е7.
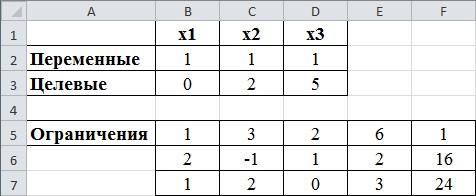
рис.2.3. Определение ограничений
Предварительные действия завершены. Вызываем надстройку «Поиск решения» в меню «Данные».
На первом этапе оптимизируем первую целевую функцию. После открытия окна «Поиск решения» в поле «Оптимизировать целевую функцию» ставим курсор и делаем ссылку на ячейку «В3», щелкая по ней мышью. В окне появится $B$3. В связи с тем, что целевая функция максимизируется, далее нужно проверить, что флажок ниже поля стоит напротив надписи «Максимум».
После ставим курсор в поле «Изменяя ячейки переменных» и обводим ячейки с переменными В2, С2 и D2, выделяя ячейки с переменными. В поле появиться $B$2:$D$2.
В нижней части окна находится поле «Ограничения». Для того, чтобы ввести ограничения, нажимаем кнопку «Добавить», откроется окно «Добавление ограничения». В левом поле «Ссылка на ячейки» вводят ссылку на левую часть первого ограничения – ячейку «Е5», в центральном окне определяем знак«»и в правом «Ограничения» выбираем соответствующую правую часть первого ограничения –«F5». Нажимаем «ОК», видим, что ограничение появилось в окне. Нажимаем вновь «Добавить», вводим «E6» «» и «F6». Вновь нажимаем «Добавить», вводим «E7» «≤» и «F7».
Для ввода дополнительных ограничений вновь нажимаем «Добавить», ставим курсор в левое поле и обводим ячейки В2, С2 и D2 (результат $B$2:$D$2) в среднем окне ставим «» и в правом число 0.
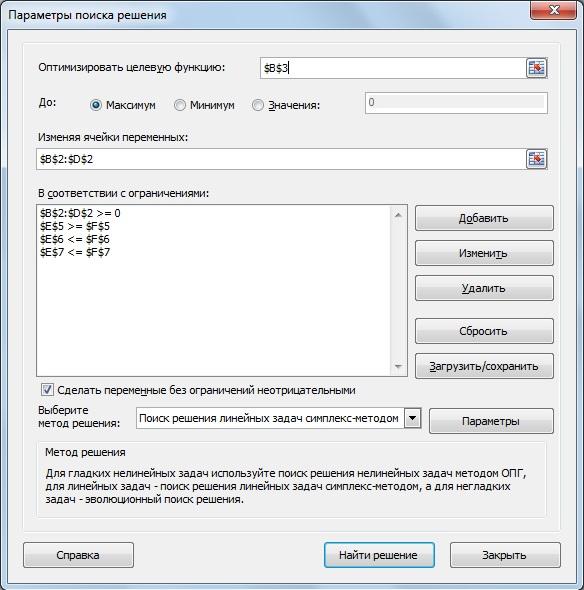
рис. 2.4. Параметры поиска решения
Далее выбираем метод решения «Поиск решения линейных задач симплекс-методом». Для запуска вычислений нажимаем кнопку «Найти решение». Появляется надпись, что решение найдено.

Выбираем «Сохранить найденное решение» и «ОК» видим результат. В ячейках В2, С2 и D2 видны значения переменных соответствующие оптимальному решению: 11,2; 6,4 и 0. В ячейки В3 – значение целевой функции 28,8.
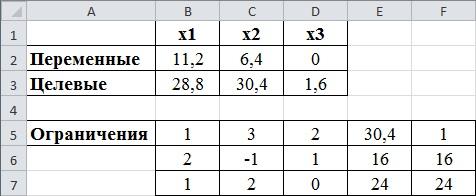
рис.2.5. Результат полученного решения
Вызываем надстройку «Поиск решения», видно, что все прежние данные остались введенными. Меняем ссылку на целевую функцию. Ставим курсор в поле «Оптимизировать целевую функцию» и щелкаем по ячейке С3, в которой находится ссылка на вторую целевую функцию. Так, как вторая целевая минимизируется, то ставим флажок в поле напротив надписи «Минимум». Вводим дополнительное ограничение, связанное с уступкой по первому критерию. Переводим курсор в поле «Ограничения» и нажимаем кнопку «Добавить», правее поля. В появившемся окне «Добавление ограничения» в трех окнах (слева на право) вводим данные «В3», «≥», «С9».

Результат – переменные равны 10,2; 4,4; 0. Вторая целевая функция равна 23,4 (ячейка С3). Первая равна своему минимальному значению 24,8 (ячейка В3).
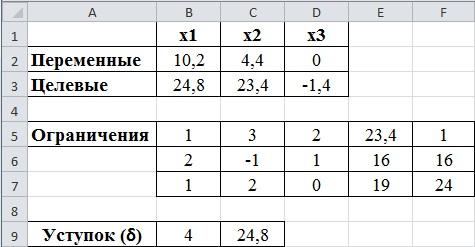
рис.2.6. Определение уступка

На третьем этапе делаем уступку по второму критерию. Величина уступки равна . Так, как вторая функция минимизируется, то ее значение не должно превышать 23,4+5=28,4. Вызываем надстройку «Поиск решения». Меняем ссылку на целевую функцию. Ставим курсор в поле «Оптимизировать целевую функцию» и щелкаем по ячейке D3, в которой находится ссылка на третью целевую функцию. Так, как третья целевая максимизируется, то ставим флажок в поле напротив надписи «Максимум». Вводим дополнительное ограничение, связанное с уступкой по второму критерию. Переводим курсор в поле «Ограничения» и нажимаем кнопку «Добавить». В появившемся окне «Добавление ограничения», вводим данные «С3», «≤», «С10».

Результат – переменные равны 10,76; 6,62; 1,11. Целевые функции равны, соответственно, 24,8; 28,4 и 6,93. Это окончательный ответ. Все дополнительные условия соблюдены.
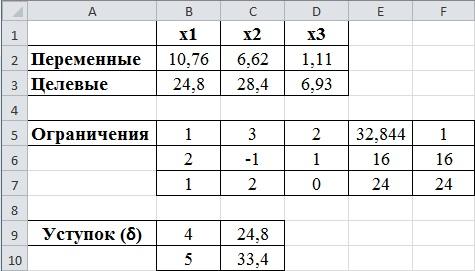
рис.2.7. Окончательный результат решения по методу последовательного уступка
Читайте также:

