Метод искусственного базиса в excel

Обновлено: 07.07.2024

Недавно появилась необходимость создать с нуля программу, реализующую алгоритм симплекс-метода. Но в ходе решения я столкнулся с проблемой: в интернете не так уж много ресурсов, на которых можно посмотреть подробный теоретический разбор алгоритма (его обоснование: почему мы делаем те или иные шаги) и советы по практической реализации — непосредственно, алгоритм. Тогда я дал себе обещание — как только завершу задачу, напишу свой пост на эту тему. Об этом, собственно, и поговорим.

Замечание. Пост будет написан достаточно формальным языком, но будет снабжен комментариями, которые должны внести некоторую ясность. Такой формат позволит сохранить научный подход и при этом, возможно, поможет некоторым в изучении данного вопроса.

§1. Постановка задачи линейного программирования

Определение: Линейное программирование – математическая дисциплина, посвященная теории и методам решения экстремальных задач на множествах n- мерного пространства, задаваемых системами линейными уравнений и неравенств.

Общая задача линейного программирования (далее – ЛП) имеет вид:

§2. Каноническая форма задачи ЛП

Каноническая форма задачи ЛП:

Замечание: Любая задача ЛП сводится к канонической.

Алгоритм перехода от произвольной задачи ЛП к канонической форме:

Неравенства с отрицательными умножаем на (-1).
Если неравенство вида (≤), то к левой части добавляем – добавочную переменную, и получаем равенство.
Если неравенство вида (≥), то из левой части вычитаем , и получаем равенство.
Делаем замену переменных:

Если , то
Если — любой, то , где

§3. Угловые точки. Базисные/свободные переменные. Базисные решения

Определение: Точка называется угловой точкой, если представление возможно только при .

Иными словами, невозможно найти две точки в области, интервал проходящий через которые содержит (т.е. – не внутренняя точка).

Графический способ решения задачи ЛП показывает, что нахождение оптимального решения ассоциируется с угловой точкой. Это является основной концепцией при разработке симплекс-метода.

Определение: Пусть есть система m уравнений и n неизвестных (m < n). Разделим переменные на два множества: (n-m) переменные положим равными нулю, а остальные m переменных определяются решением системы исходных уравнений. Если это решение единственно, то тогда ненулевые m переменных называют базисными; нулевые (n-m) переменных – свободными (небазисными), а соответствующие результирующие значения переменных называют базисным решением.

§4. Симплекс-метод

Симплекс-метод позволяет эффективно найти оптимальное решение, избегая простой перебор всех возможных угловых точек. Основной принцип метода: вычисления начинаются с какого-то «стартового» базисного решения, а затем ведется поиск решений, «улучшающих» значение целевой функции. Это возможно только в том случае, если возрастание какой-то переменной приведет к увеличению значения функционала.

Необходимые условия для применения симплекс-метода:

Задача должна иметь каноническую форму.
У задачи должен быть явно выделенный базис.

Замечание: Базисный вектор имеет размерность (m*1), где m – количество уравнений в системе ограничений.

Для удобства вычислений и наглядности обычно пользуются симплекс-таблицами:

В первой строке указывают «наименование» всех переменных.
В первом столбце указывают номера базисных переменных, а в последней ячейке – букву Z (это строка функционала).
В «середине таблицы» указывают коэффициенты матрицы ограничений — aij.
Последний столбец – вектор правых частей соответствующих уравнений системы ограничений.
Крайняя правая ячейка – значение целевой функции. На первой итерации ее полагают равной 0.

Замечание: Если ограничения в исходной задаче представлены неравенствами вида ≤, то при приведении задачи к канонической форме, введенные дополнительные переменные образуют начальное базисное решение.

Замечание: Коэффициенты в строке функционала берутся со знаком “-”.

Алгоритм симплекс-метода:

1. Выбираем переменную, которую будем вводить в базис. Это делается в соответствии с указанным ранее принципом: мы должны выбрать переменную, возрастание которой приведет к росту функционала. Выбор происходит по следующему правилу:

Если задача на минимум – выбираем максимальный положительный элемент в последней строке.
Если задача на максимум – выбираем минимальный отрицательный.

Замечание: Хотя мы и берем минимальное отрицательное число в задаче на максимум, этот коэффициент показывает направление роста функционала, т.к. строка функционала в симплекс-таблице взята со знаком “-”. Аналогичная ситуация с минимизацией.

Определение: Столбец симплекс-таблицы, отвечающий выбранному коэффициенту, называется ведущим столбцом.

2. Выбираем переменную, которую будем вводить в базис. Для этого нужно определить, какая из базисных переменных быстрее всего обратится в нуль при росте новой базисной переменной. Алгебраически это делается так:

Вектор правых частей почленно делится на ведущий столбец
Среди полученных значений выбирают минимальное положительное (отрицательные и нулевые ответы не рассматривают)

Замечание: Фактически, мы выражаем старые базисные переменные из каждого уравнения системы ограничений через остальные переменные и смотрим, в каком уравнении возрастание новой базисной переменной быстрее всего даст 0. Попадание в такую ситуацию означает, что мы «наткнулись» на новую вершину. Именно поэтому нулевые и отрицательные элементы не рассматриваются, т.к. получение такого результата означает, что выбор такой новой базисной переменной будет уводить нас из области, вне которой решений не существует.

3. Ищем элемент, стоящий на пересечении ведущих строки и столбца.

Определение: Такой элемент называется ведущим элементом.

4. Вместо исключаемой переменной в первом столбце (с названиями базисных переменных) записываем название переменной, которую мы вводим в базис.

5. Далее начинается процесс вычисления нового базисного решения. Он происходит с помощью метода Жордана-Гаусса.

Новая Ведущая строка = Старая ведущая строка / Ведущий элемент
Новая строка = Новая строка – Коэффициент строки в ведущем столбце * Новая Ведущая строка

6. После этого проверяем условие оптимальности. Если полученное решение неоптимально – повторяем весь процесс снова.

§5. Интерпретация результата работы симплекс-метода

1. Оптимальность

Условие оптимальности полученного решения:

Если задача на максимум – в строке функционала нет отрицательных коэффициентов (т.е. при любом изменении переменных значение итогового функционала расти не будет).
Если задача на минимум – в строке функционала нет положительных коэффициентов (т.е. при любом изменении переменных значение итогового функционала уменьшаться не будет).

Однако, стоит отметить, что заданный функционал может не и достигать максимума/минимума в заданной области. Алгебраический признак этого можно сформулировать следующим образом:

При выборе ведущей строки (исключаемой переменной) результат почленного деления вектора правых частей на ведущий столбец содержит только нулевые и отрицательные значения.

Фактически, это значит, что какой бы рост мы не задавали новой базисной переменной, мы никогда не найдем новую вершину. А значит, наша функция не ограничена на множестве допустимых решений.

3. Альтернативные решения

При нахождении оптимального решения возможен еще один вариант – есть альтернативные решения (другая угловая точка, дающая то же самое значение функционала).

Алгебраический признак существования альтернативы:

После достижения оптимального решения имеются нулевые коэффициенты при свободных переменных в строке функционала.

Это значит, что при росте соответствующей переменной с нулевым коэффициентом значение функционала не изменится и новое базисное решение будет также давать оптимум функционала.

Эпилог

Данная статья направлена на более глубокое понимание теоретической части. В замечаниях и пояснениях здесь можно получить ответы на вопросы, которые обычно опускают при изучении этого метода и принимают априори. Однако, надо понимать, что многие методы численной оптимизации основаны на симплекс-методе (например, метод Гомори, М-Метод) и без фундаментального понимания вряд ли получится сильно продвинуться в дальнейшем изучении и применении всех алгоритмов этого класса.

Чуть позже напишу статью о практической реализации симплекс-метода, а также несколько статей о Методе искусственных переменных (М-Метод), Методе Гомори и Методе ветвей и границ.

В Excel 2007 для включения пакета анализа надо нажать перейти в блок Параметры Excel, нажав кнопку в левом верхнем углу, а затем кнопку «Параметры Excel» внизу окна:

Далее в открывшемся списке нужно выбрать Надстройки, затем установить курсор на пункт Поиск решения, нажать кнопку Перейти и в следующем окне включить пакет анализа.

Загрузите файл шаблон для проверки в Excel
Откройте его в MS Excel
Мышкой или с помощью клавиатуры перейдите к ячейке G4
Выполните команду Сервис / Поиск решения

Значение переменных X_i может различаться, но целевая функция F(x) должна иметь такое же значение.

Иногда задание звучит следующим образом: расчеты осуществить на ЭВМ, привести распечатку полученных результатов.

Результаты (Answer). В отчет включаются исходные и конечные значения целевой и влияющих ячеек, дополнительные сведения об ограничениях.
Устойчивость (Sensitivity). Отчет, содержащий сведения о чувствительности решения к малым изменениям в изменяемых ячейках или в формулах ограничений.
Пределы (Limits). Помимо исходных и конечных значений изменяемых и целевой ячеек в отчет включаются верхние и нижние границы значений, которые могут принимать влияющие ячейки при соблюдении ограничений.

Пример. В библиотеке работают 6 пожилых уборщиц. Каждая из них по своим физическим возможностям и состоянию здоровья может выполнять только определенные виды работ, причем с определенной производительностью. Площадь каждой из работ известна. Нужно добиться минимума времени на уборку помещений.

Задание. Реализуйте все нижеприведенные шаги в табличном процессоре Excel, необходимые для решения задачи ЛП табличным симплекс-методом, применяя метод искусственного базиса.

Поясним последовательность действий при решения задачи ЛП методом искусственного базиса (М-методом) на примере.

Задача. Решить задачу табличным симплекс-методом [8].

Порядок выполнения работы:

I. Проверка выполнения условий, необходимых для решения задачи табличным симплекс-методом.

Задача не является канонической, приведите ее к канонической форме.

Переведите исходную функцию на максимум.

Избавьтесь от неравенств во втором и третьем ограничении способом, указанным в 2.1.

В ограничениях 1 и 2 есть базисные переменные: - в первом,- во втором, в третьем ограничении нет базисной переменной, следовательно, необходимо применить М-метод.

Составьте расширенную задачу, добавив искусственные переменные к тем ограничениям, где нет базисных переменных.

Расширенная задача:

В целевой функции расширенной задачи есть базисные переменные. Выполните условие, выразив базисные переменные ичерез небазисные. Подставьте выражения в целевую функцию.

Таким образом, получите задачу линейного программирования, для которой выполняются все 4 условия.

II. Оформление исходных данных.

Откройте табличный процессор Excel и введите заголовок Метод искусственного базиса.

Заполните начальную симплекс-таблицу, таким же образом как в лабораторной работе №4, добавив в нее столбец для переменной и-строку (рис. 42).

Рис. 42. Исходная симплекс таблица.

Проконтролируйте правильность заполнения таблицы. Так как ,,- базисные переменные, то на пересечении(5 строка) с (столбецF) должна стоять 1 (ячейка F5), а в соответствующем столбце ниже – нули, на пересечении (6 строка) с (столбецG) должна стоять 1 (ячейка G6), а в соответствующем столбце ниже – нули, (7 строка) с (столбецI) должна стоять 1 (ячейка I7), а в соответствующем столбце ниже – нули.

Запишите значение целевой функции, начальный опорный план, опираясь на столбец свободных членов (рис. 43).

Рис. 43. Значение целевой функции и начальный опорный план.

III. Нахождение оптимального плана и оптимального значения целевой функции.

Так в индексной строке есть отрицательный коэффициент при переменной, то опорный план не является оптимальным. Организуйте процесс улучшения плана, выполнив предложенные шаги.

В индексной строке найдите отрицательные элементы. Составьте выражения, учитывая -строку. Получите.

В данном случае один отрицательный элемент – это выражение , которое соответствует переменной.

Соответствующий столбец назовите ведущим. Данный столбец показывает, какую переменную необходимо включить в базис (рис. 44).

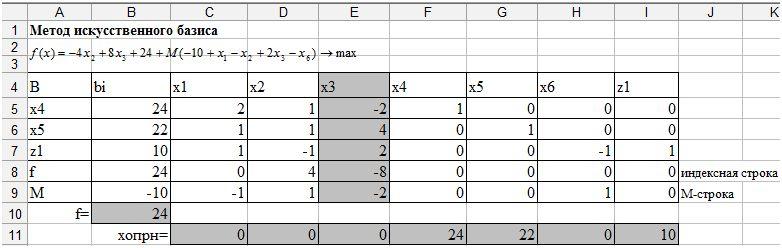
Рис. 44. Ведущий столбец.

Определите какую переменную необходимо исключить из базиса. Для этого составьте отношения для всех элементов столбца свободных членов () к соответствующим элементам ведущего столбца (). Найдите ведущую строку и ведущий элемент (рис. 45).

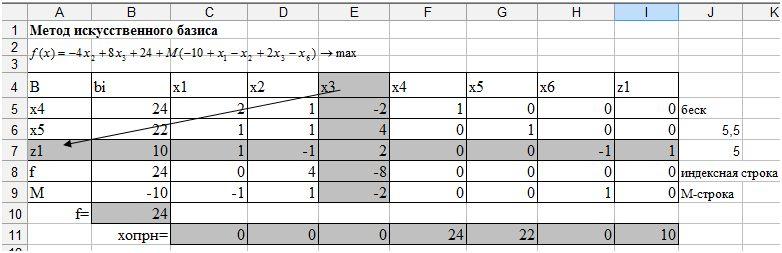
Рис. 45. Ведущая строка и ведущий столбец.

Постройте новую симплексную таблицу. Выведите переменную из базиса, на ее место запишите ту переменную, которой соответствует ведущий столбец. Выполните симплексные преобразования, таким же образом, как и в лабораторной №4, получите базисный столбец, который соответствует переменной. Значения столбцаможно удалить, так как переменная вышла из базиса (рис. 46).

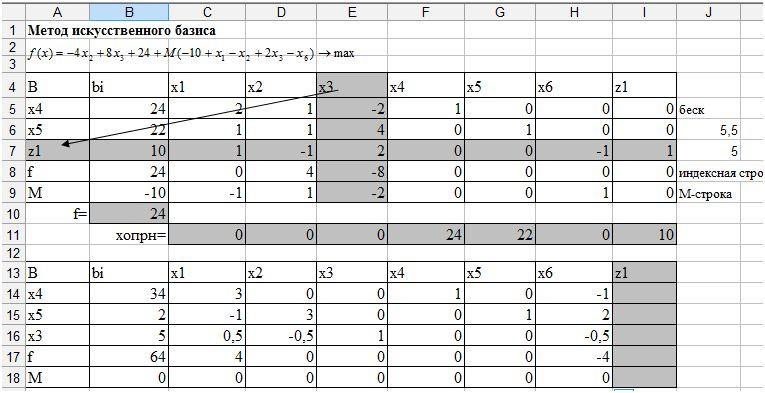
Рис. 46. Первая и вторая симплексные таблицы.

Так как в -строке все нули, то ее можно удалить из таблицы и получить таблицу, в которой будет только функция(рис. 47).

Рис. 47. Симплексная таблица.

В индексной строке есть отрицательные коэффициенты при переменных, опорный план не является оптимальным.

Запишите значение целевой функции, найденный новый опорный план, опираясь на столбец свободных членов (рис. 48). Проконтролируйте, что значение целевой функции максимизируется.

Организуйте процесс улучшения плана, выполнив те же шаги, до тех пор, пока не будет выполняться какой-нибудь из критериев остановки, получите новую таблицу (рис. 48).

Рис. 48. Симплексные таблицы.

В индексной строке нет отрицательных элементов, поэтому план оптимален,. Так как в исходной задаче функция стремится к минимуму, то

Задание. Воспользуйтесь материалами лабораторной работы №3. Выполните проверку, используя программу MathCad.

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Освоение технологии решения задач линейного программирования симплекс-методом в табличном процессоре Excel.

Содержание лабораторной работы.

Дана задача линейного программирования. Требуется найти решение ЗЛП в табличном процессоре EXCEL симплекс – методом.

Задание на лабораторную работу.

Задача:

На арендном предприятии для изготовления двух типов кабеля Аи В выполняется пять технологических операций. Нормы затрат времени на изготовление1000 м кабеля каждого вида по каждой операции, доход от реализации 1000 м кабеля, а также общий фонд рабочего времени по каждой операции приведены в табл. 4.5. Определить оптимальный выпуск продукции, при котором будет получен наибольший доход.

Вид технологической операции

Нормы затрат времени для производства кабеля

Общий фонд времени

Доход от реализации

→max

Избавимся от неравенств в ограничениях, введя в ограничения неотрицательные балансовые переменные, и перейдём к каноническому виду:

→max

Составим опорный план

Теперь выберем разрешающий столбец. В нашем случае это столбец С, поскольку в нём находится наибольшее положительное значение целевой функции. После этого выбираем разрешающий элемент( min i/a_ij>), в нашем случае это элемент С7.

Далее составляем новую симплекс – таблицу, в которой элементы разрешающей строки делятся на разрешающий элемент. Элементы разрешающей строки и столбца становятся равны 0, кроме разрешающего элемента. Остальные элементы определяются по правилу прямоугольника (сумма произведений главной и побочной диагонали делить на разрешающий элемент).

В новой симплекс – таблице значения целевой функции равны нулю или меньше нуля, а это значит, что найдено оптимальное решение:

Ответ: для достижения максимального дохода, который составит 26 ед. необходимо выпустить 2 единицы изделий типа А и отказаться от выпуска изделий типа В.

Ответы на контрольные вопросы.

1. Как построить первоначальный опорный план задачи линейного программирования?

Для построения опорного плана необходимо построить модель ЗЛП в каноническом виде и преобразовать её в симплекс – таблицу для дальнейших преобразований.

2. Перечислите условия оптимальности опорного плана.

План считается оптимальным, если в строке целевой функции симплекс – таблицы все элементы равны нулю или меньше него. Если есть положительные числа, то необходимо перейти к новому опорному плану, который даст более оптимальное значение.

3. Как определяется вектор для включения в базис, если первоначальный план неоптимальный?

Для определения разрешающего столбца нужно, для задачи на максимум, в целевой строке выбрать из отрицательных элементов наибольший по модулю, а в задаче на минимум выбрать наибольший положительный элемент. Столбец, в котором расположен выбранный элемент и будет являться разрешающим.

4. Когда линейная функция не ограничена на многограннике решений?

Если существует такая угловая точка многогранника решений, в которой линейная функция задачи линейного программирования достигает своего оптимума, то эта точка называется оптимальным решением, если такой точки нет, значит функция не ограничена на многограннике решений.

5. Как определить вектор, подлежащий исключению из базиса?

Чтобы определить вектор подлежащий исключению из базиса, необходимо найти отношение свободных членов к элементам разрешающего столбца. Строку с наименьшим отношением исключают.

Элемент, расположенный на пересечении разрешающей строки и разрешающего столбца называется разрешающим.

6. Какой метод решения систем линейных уравнений лежит в основе симплексного метода?

В основе решения задач линейного программирования лежит метод замещения одного опорного плана другим, в котором целевая функция достигает своего оптимального значения. Указанное замещение возможно, если известен некоторый исходный опорный план.

7. Какую простейшую геометрическую интерпретацию можно дать симплексному методу?

Геометрической интерпретацией симплексного метода является выпуклый многогранник.

Читайте также: