Метод квадратур гаусса excel интеграл

Обновлено: 07.07.2024

Задание: Вычислить определенный интеграл, используя квадратурную формулу Гаусса с тремя узлами для числа разбиения отрезка интегрирования n=1. Определить погрешность результата.

Подынтегральная функиция: ln(x)
Нижний предел: 1
Верхний предел: 2.7

Помогите, пожалуйста, написать прогу. все облазил, ничего по этой теме не нашел.

__________________
Помощь в написании контрольных, курсовых и дипломных работ здесь

Вычисление интеграла по квадратурной формуле Гаусса
Помогите, пожалуйста. Не нашел ничего схожего к требуемому заданию. Необходимо вычислить интеграл.

Программа для вычисления интеграла по квадратурной формуле Гаусса
Помогите составить программу на Паскале для вычисления интеграла функции x-0,5/sqrt (sqr(x)-1) по.

Зависит ли от выбора квадратурной формулы решение интеграла?
Всем привет. Мне нужно разложить ф-цию в ряд Фурье-Лагерра с помощью полинома Чебышева-Лагерра.

приближенного вычисления двойного интеграла, основанный на применении квадратурной формулы Симпсона
доброй вечер, помогите найти ошибку в программе, вроде все делаю правильно а результат выходит.

Чет прочитал, многое не понял. Там только вычисление узлов и весов этой формулы. про вычисление с помошью нее интеграла ничего не написано. ап!
Есть такая же задача, выше ссылки прочитал, но там скачал че т не понятно где и куда файлов куча, смысл понял, но незнаю как вогнать в паскал потому что вообще не знаю его не команды ничего. в общем вот условие.
Вычислить определенный интеграл, используя квадратурную формулу Гаусса с 4 узлами для числа разбиения отрезка интегрирования n=6
функиция: xL^x
Нижний предел: 0
Верхний предел: 1
да и функция какая то xl я незнаю даж как правильно ее вписать в паскаль =(
Вообщем помогите чайнику, мне хотя бы или написать программу ну или на край хотя бы написанная на паскале уже готовая программа очень похожая что бы, что там поменять(дописать) может сам додумаю( не подумайте что я халявщик, просто в интернете написанных программ на эту тему готовых я не нашел даже подобных.
на край если никто не хочет помоч бесплатно, могу на мобильный оплатить немного.
просто край нужно, хвост уже год висит ну пусть фунция будет arcsinx например, хоть даже с такой написать Tinager, Вы наверное не на дворника учитесь и наверное это должны знать. Я например первый раз о таком услышал из этой темы и ради вас не собираюсь это изучать.

Кстати тема интересная. Вот моя функция вычисления. Константы взяты из какого-то справочника или учебника, ща уже не помню даже.

Tronix, спасибо большое.

По формуле Гаусса при n = 3 вычислить интеграл
на matlabe По формуле Гаусса при n = 3 вычислить интеграл

Вычислить поверхностный интеграл по формуле Гаусса — Остроградского
\iint_ (r , n) \operatornameb D: замкнутое пространство, полученное с помощью пространств.

Используя формулы центральных прямоугольников вычислить интеграл

В статье подробно, вплоть до самых мелочей, рассмотрены три способа взятия интеграла Эйлера-Пуассона. В одном из способов выводится вспомогательная формула редукции. Для нахождения некоторых сложных интегралов можно использовать формулы редукции, которые позволяют понизить степень подынтегрального выражения и вычислить соответствующие интегралы за конечное число шагов.

Данный интеграл берется от гауссовой функции:
Здесь есть очень интересный математический способ. Чтобы найти исходный интеграл, сначала ищут квадрат этого интеграла, а потом от результата берут корень. Почему? Да потому что так гораздо проще и безболезненно можно перейти в полярный координаты. Поэтому, рассмотрим квадрат Гауссового интеграла:

Мы видим, что у нас получается двойной интеграл от некоторой функции . В конце этого поверхностного интеграла стоит элемент площади в декартовой системе координат .
Теперь давайте переходить в полярную систему координат:

Тут нужно заметить, что r может изменяться в пределах от 0 до +∞, т.к. x изменялось в таких же пределах. А вот угол φ изменяется от 0 до π/2, что описывают область интегрирования в первой четверти декартовой системы координат. Подставляя в исходный, получим:

В силу симметричности интеграла и положительной области значений подынтегральной функции, можно заключить, что

Давайте поищем ещё какие-нибудь решения? Это ведь интересно! :)

Рассмотрим функцию
А теперь вспомним школьную математику и проведем простейшее исследование функции с помощью производных и пределов. Не то, чтобы мы здесь будем считать сложные пределы (ведь в школе их не проходят), а просто порассуждаем что будет с функцией, если её аргумент стремится к нулю или к бесконечности, таким образом прикинем асимптотическое поведение, что в математике всегда очень важно. Это похоже на качественную оценку того, что происходит.

Она ограничена сверху единицей на интервале (-∞;+∞) и нулем на интервале [-1;+∞).

Cделаем следующую замену переменных
И получим:

Ограничим в первом неравенстве изменение (0,1), а во втором — промежутком (0;+∞), возведём оба неравенства в степень n, так как неравенства с положительными членами можно возводить в любую положительную степень. Получим:

Давайте для наглядного доказательства неравенств построим графики при n = 1

Теперь попробуем проинтегрировать неравенства в пределах, которые указаны в соответствующих системах. И сразу объединим всё в одно неравенство:

Опять таки, если посмотреть на графики, то данное неравенство справедливо.

С учетом небольшой замены, легко увидеть, что:

Т.е. в том большом неравенстве в середине у нас интеграл Эйлера-Пуассона, а вот теперь нам нужно найти интегралы, которые стоят на границах данного неравенства.

Найдем интеграл от левой границы:

Для того, чтобы его посчитать и оценить, давайте сначала найдем интеграл общего вида. Сейчас я покажу вам как можно вывести формулу редукции ( в математике под такими формулами подразумевают понижения степени ) для данного интеграла.

Теперь если с помощью формулы редукции рассмотреть тот же интеграл, но с нашими пределами от 0 до π/2, то можно сделать некоторые упрощения:

Как мы видим, понижать можно до бесконечности (зависит от n). Однако, и тут есть одна тонкость. Формула изменяется в зависимости то того, является ли n четным числом или не является.
Для этого рассмотрим два случая.

Где n!! — двойной факториал. Двойной факториал числа n обозначается n!! и определяется как произведение всех натуральных чисел в отрезке [1, n], имеющих ту же чётность что и n

В силу того, что 2n+1 — нечетное число при любом значении n, получим для левой границы нашего неравенства:

Найдем интеграл от правой границы:
(здесь используем ту же формулу редукции, которую доказали ранее)

После того, как мы оценили левую и правую части неравенства, сделаем некоторые преобразования, чтобы оценить пределы левой и правой частей неравенства при условии, что n стремится к ∞:

Возведем обе части неравенства в квадрат:

Теперь сделаем небольшое лирическое отступление. В 1655 году Джон Валлис (английский математик, один из предшественников математического анализа.) предложил формулу для определения числа π. Дж. Валлис пришёл к ней, вычисляя площадь круга. Это произведение сходится крайне медленно, поэтому для практического вычисления числа π формула Валлиса мало пригодна. Но для оценки нашего выражения она отлично подходит :)

Теперь преобразуем наше неравенство так, чтобы мы могли увидеть где подставить формулу Валлиса:

Из формулы Валлиса следует, что и левое, и правое выражение стремятся к π/4 при n → ∞
В силу того, что функция exp[-x²] является четной, мы смело полагаем, что

Впервые одномерный гауссов интеграл вычислен в 1729 году Эйлером, затем Пуассон нашел простой приём его вычисления. В связи с этим он получил название интеграла Эйлера — Пуассона.

Давайте еще попробуем вычислить Гауссов интеграл. Его можно написать в разных видах. Ведь ничего не меняет изменение название переменной, по которой идет интегрирование.

Можно перейти от трехмерных декартовых к сферическим координатам и рассмотреть куб интеграла Гаусса.

Якобиан этого преобразования можно посчитать следующим образом:

Посчитаем интегралы последовательно, начиная с внутреннего.

Тогда в результате получим:

Интеграл Эйлера-Пуассона часто применяется в теории вероятностей.

Надеюсь, что для кого-нибудь статья будет полезной и поможет разобраться в некоторых математических приемах :)

Давайте разберёмся, как вычислить определённый интеграл таблично заданной функции с помощью программы Excel из состава Microsoft Office.

1 Инструкция по нахождению определённого интегралав программе Microsoft Excel

1 Постановка физической задачина расчёт определённого интеграла

Допустим, у нас есть таблично заданная некоторая величина. Для примера пусть это будет накопленная доза радиации при авиаперелёте. Скажем, был такой эксперимент: человек с дозиметром летел на самолёте из пункта А в пункт Б и периодически измерял дозиметром мощность дозы (единицы измерений – микрозиверт в час, мкЗв/ч). Возможно, Вас это удивит, но при обычном перелёте на самолёте человек попадает под радиоактивное излучение, превышающее фоновый уровень до 10 раз и даже больше. Но воздействие это кратковременное, и поэтому не столь опасное. По результатам измерений у нас есть таблица вот такого формата: Время – Мощность дозы.

Таблично заданная величина для расчёта определённого интеграла

Необходимо посчитать суммарную накопленную за время полёта дозу.

2 Геометрический смыслопределённого интеграла

Как мы помним из курса школьной алгебры, определённый интеграл – это площадь под графиком измеряемой величины. Чтобы определить накопленную дозу радиации в рассматриваемом примере, нужно определить площадь фигуры под графиком таблично заданной мощности дозы. Накопленная доза радиации равна площади фигуры под графиком мощности дозы

График изменения мощности дозы во время полёта

3 Методика вычисленияопределённого интеграла

Вычислять интеграл мы будем самым простым, но довольно точным методом – методом трапеций. Напомню, площадь фигуры под графиком любой кривой можно разделить на прямоугольные трапеции. Сумма площадей этих трапеций и будет искомым значением определённого интеграла.

Площадь трапеции определяется как полусумма оснований, умноженная на высоту: S_трап = (A + B) / 2 × h Основания в нашем случае – это табличные измеренные значения мощности дозы за 2 последовательных промежутка времени, а высота – это разница времени между двумя измерениями.

Метод трапеций для вычисления значения определённого интеграла

4 Согласованиеединиц измерения

В нашем примере измерения мощности дозы радиации даётся в мкЗв/час, а шкала времени – с точностью до минут. Мы не можем брать интеграл по времени, измеряемому в минутах, для величины, измеряемой в часах. Поэтому необходимо перевести мкЗв/час в мкЗв/мин.

Для перевода просто разделим мощность дозы в мкЗв/час построчно на количество минут в часе, т.е. на 60. Добавим ещё один столбец в нашу таблицу. На иллюстрации это столбец "D". В столбце "D" в строке 2 вписываем =С2/60 А потом с помощью маркера заполнения распространяем эту формулу на все остальные ячейки в столбце "D", (т.е. тянем мышью чёрный прямоугольник в правом нижнем углу ячейки). Таким образом, в столбце "D" у нас появятся значения мощности дозы радиации, измеряемые в микрозивертах в минуту для каждой минуты перелёта.

Согласуем единицы измерения по шкале времени и шкале мощности дозы

5 Вычисление площадей отдельных трапеций

Теперь нужно найти площади трапеций за каждый промежуток времени. В столбце "E" будем вычислять по приведённой выше формуле площади трапеций. Полусумма оснований – это половина суммы двух последовательных мощностей дозы из столбца "D". Так как данные идут с периодом 1 раз в минуту, а мы берём интеграл по времени, выраженному в минутах, то высота каждой трапеции будет равна единице (разница времени между каждыми двумя последовательными измерениями, например, 17ч31мин — 17ч30мин = 0ч1мин = 1мин).

Получаем формулу в ячейке "E3": =1/2*(D3+D2)*1. Понятно, что "×1" в этой формуле можно не писать. И аналогично, с помощью маркера заполнения, распространяем формулу на весь столбец. Теперь в каждой ячейке столбца "Е" посчитана накопленная доза за 1 минуту полёта.

Вычисление площадей прямоугольных трапеций за каждый промежуток времени

Если бы данные шли не через 1 минуту, то нам нужно было бы написать формулу так:
=1/2*(D3+D2)*(МИНУТЫ(A3) – МИНУТЫ(A2)).
Правда при этом, если есть переход на следующий час, то получится отрицательное значение. Чтобы этого не произошло, впишем в формулу часы:
=1/2*(D3+D2)*(ЧАС(A3)*60+МИНУТЫ(A3)) – (ЧАС(A2)*60+МИНУТЫ(A2)).
Если переходим на следующие сутки, то нужно будет уже добавлять даты, и т.д.

5 Определение площадипод графиком функции

Осталось найти сумму вычисленных площадей трапеций. Можно в ячейке "F2" написать формулу: =СУММ(E:E) Это и будет сумма всех значений в столбце "E", т.е. численное значение искомого определённого интеграла. Но давайте сделаем вот что: определим накопленную дозу в разные моменты полёта. Для этого в ячейку "F4" впишем формулу =СУММ(E$3:E4) и маркером заполнения распространим на весь столбец "F".

Обозначение E$3 говорит программе Excel, что увеличивать индекс ячейки "3" в столбце "E" при переносе формулы на следующие строки не нужно. Т.е. в строке 4 формула будет определять сумму в ячейках с "Е3" по "Е4", в строке 5 – сумму с "Е3" по "Е5", в строке 6 – с "Е3" по "Е6" и т.д.

Построим график по столбцам "F" и "A". Это график изменения накопленной дозы радиации во времени. Наглядно видно монотонное увеличение накопленной дозы радиации за время полёта. Это говорит о том, что мы правильно рассчитали интеграл. И окончательное значение накопленной за двухчасовой полёт дозы радиации, которое получается в последней ячейке этого столбца, равно примерно 4,5 микрозиверт.

Вычисление суммарной площади всех трапеций, что численно равно искомому определённому интегралу

Таким образом, мы только что нашли определённый интеграл таблично заданной функции в программе Excel на реальном физическом примере. В качестве приложения к статье – файл Excel с нашим примером.

Назначение сервиса . Сервис предназначен для онлайн вычисления определенного интеграла по формуле прямоугольников.

Правила ввода функции

Формула средних прямоугольников

Это самая простая квадратурная формула вычисления интеграла, в которой используется одно значение функции
(1)
где ; h=x₁-x₀.
Формула (1) представляет собой центральную формулу прямоугольников. Вычислим остаточный член. Разложим в ряд Тейлора функцию y=f(x) в точке ε₀:
(2)
где ε₁[x,ε₀]; x∈[x₀,x₁]. Проинтегрируем (2):
(3)

Во втором слагаемом подынтегральная функция нечетная, а пределы интегрирования симметричны относительно точки ε₀. Поэтому второй интеграл равен нулю. Таким образом, из (3) следует .
Т. к. второй множитель подынтегрального выражения не меняет знак, то по теореме о среднем получим , где . После интегрирования получим . (4)
Сравнивая с остаточным членом формулы трапеций, мы видим, что погрешность формулы прямоугольников в два раза меньше, чем погрешность формулы трапеций. Этот результат верен, если в формуле прямоугольников мы берём значение функции в средней точке.
Получим формулу прямоугольников и остаточный член для интервала [a, b]. Пусть задана сетка x_i=a+ih, i=0,1. n, h=x_i+1-x_i . Рассмотрим сетку ε_i=ε₀+ih, i=1,2. n, ε₀=a-h/2. Тогда . (5)
Остаточный член .
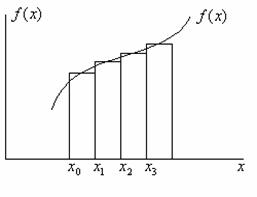
Геометрически формула прямоугольников может быть представлена следующим рисунком:

Если функция f(x) задана таблично, то используют либо левостороннюю формулу прямоугольников (для равномерной сетки)

либо правостороннюю формулу прямоугольников

.
Погрешность этих формул оценивается через первую производную. Для интервала [x₀, x₁] погрешность равна

Читайте также: