Как найти соотношение сторон треугольника

Обновлено: 04.07.2024

Соотношение сторон в треугольнике всегда подчиняется следующему правилу:длина любой стороны треугольника не может быть больше суммы длин двух других сторон.

Это правило так же называется теоремой о неравенстве треугольника. С помощью этой теоремы можно для любых трех сторон ответить на вопрос: можно ли из них построить треугольник?

Существует ли треугольник со сторонами 3, 4, 5?

Необходимо сравнить каждую сторону с суммой длин двух других.

Возьмем сторону длиной 3. Тогда сумма длин двух других сторон равна: 4 + 5 = 9; 3 < 9.

Возьмем сторону длиной 4. Тогда сумма длин двух других сторон равна: 3 + 5 = 8; 4 < 8.

Возьмем сторону длиной 5. Тогда сумма длин двух других сторон равна: 3 + 4 = 7; 5 < 7.

Во всех трех случаях правило выполняется, значит, треугольник со сторонами 3, 4, 5 существует.

Существует ли треугольник со сторонами 9, 5, 2.

Возьмем сторону длиной 9. Тогда сумма длин двух других сторон равна 5 + 2 = 7; 9 > 7.

Правило не выполняется, значит, треугольник со сторонами 9, 5, 2 построить невозможно.

Соотношение углов и сторон в треугольнике

Для любого треугольника верно следующее:

· Сумма углов треугольника равна 180°.

· Напротив большего угла лежит большая сторона треугольника.

· Напротив меньшего угла лежит меньшая сторона треугольника.

По присутствующим углам в треугольнике выделяют:

· остроугольные треугольники (содержат только острые углы);

· прямоугольные треугольники (содержат один прямой угол);

· тупоугольные треугольники (содержат один тупой угол).

Зная длины всех сторон треугольника, всегда можно определить, к какому из перечисленных типов треугольника относится данный:

· для остроугольного треугольника для всех сторон выполняется неравенство:

a2 + b2 > c2;

Докажите, что треугольник со сторонами 4, 5, 8 является тупоугольным.

Т. к. тупой угол будет наибольшим в данном треугольнике, против него должна лежать наибольшая сторона, т. е. длиной 8.

Проверим, будет ли выполняться неравенство a2 + b2 < c2, где с – сторона, лежащая против тупого угла:

Неравенство выполняется, значит, данный треугольник является тупоугольным, причем против тупого угла лежит сторона, длиной 8.

Особые треугольники

Среди всех треугольников выделяют три особых треугольника: правильный, равнобедренный, прямоугольный.

У таких треугольников есть ряд особых свойств.

Равносторонний треугольник:

· Все стороны равны.

· Все углы равны 60°.

· Биссектриса, проведенная из любого угла, является медианой и высотой.

Равнобедренный треугольник:

· Боковые стороны равны.

· Углы при основании равны.

· Высота, проведенная из вершины, является медианой и высотой.

Прямоугольный треугольник:

· Медиана, проведенная из вершины прямого угла, равна половине гипотенузы.

· Центр описанной окружности является серединой гипотенузы.

Формулы для нахождения площади треугольника

Иррациональные уравнения

Арифметический корень

Пусть n — натуральное число, отличное от единицы, а — неотрицательное число.

Арифметическим корнем n-й степени из неотрицательного числа а называетсянеотрицательное число, n-я степень которого равна а.

По определению = a.

Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

a , b , c - стороны произвольного треугольника

α , β , γ - противоположные углы

Формула длины через две стороны и угол (по теореме косинусов), ( a ):

* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение

Формула длины через сторону и два угла (по теореме синусов), ( a):

2. Как узнать сторону прямоугольного треугольника

Есть следующие формулы для определения катета или гипотенузы

a , b - катеты

c - гипотенуза

α , β - острые углы

Формулы для катета, ( a ):

Формулы для катета, ( b ):

Формулы для гипотенузы, ( c ):

Формулы сторон по теореме Пифагора, ( a , b ):

3. Формулы сторон равнобедренного треугольника

Вычислить длину неизвестной стороны через любые стороны и углы

b - сторона (основание)

a - равные стороны

α - углы при основании

β - угол образованный равными сторонами

Формулы длины стороны (основания), (b ):

Формулы длины равных сторон , (a):

4. Найти длину высоты треугольника

Высота- перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).

Высоты треугольника пересекаются в одной точке, которая называется - ортоцентр.

H - высота треугольника

a - сторона, основание

b, c - стороны

β , γ - углы при основании

p - полупериметр, p=(a+b+c)/2

R - радиус описанной окружности

S - площадь треугольника

Формула длины высоты через стороны, ( H ):

Формула длины высоты через сторону и угол, ( H ):

Формула длины высоты через сторону и площадь, ( H ):

Формула длины высоты через стороны и радиус, ( H ):

5. Формулы высоты прямого угла в прямоугольном треугольнике

В прямоугольном треугольнике катеты, являются высотами. Ортоцентр - точка пересечения высот, совпадает с вершиной прямого угла.

H - высота из прямого угла

a, b - катеты

с - гипотенуза

c₁, c ₂ - отрезки полученные от деления гипотенузы, высотой

α , β - углы при гипотенузе

Формула длины высоты через стороны, ( H ):

Формула длины высоты через гипотенузу и острые углы, ( H ):

Формула длины высоты через катет и угол, ( H ):

Формула длины высоты через составные отрезки гипотенузы , ( H ):

6. Найти длину биссектрисы в треугольнике

L - биссектриса, отрезок |OB|, который делит угол ABC пополам

a, b - стороны треугольника

с - сторона на которую опущена биссектриса

d, e - отрезки полученные делением биссектрисы

γ - угол ABC , разделенный биссектрисой пополам

p - полупериметр, p =(a+b+ c )/2

Длина биссектрисы через две стороны и угол, ( L ):

Длина биссектрисы через полупериметр и стороны, ( L ):

Длина биссектрисы через три стороны, ( L ):

Длина биссектрисы через стороны и отрезки d , e , ( L ):

Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.

7. Биссектриса прямоугольного треугольника

1. Найти по формулам длину биссектрисы из прямого угла на гипотенузу:

L - биссектриса, отрезок ME , исходящий из прямого угла (90 град)

a, b - катеты прямоугольного треугольника

с - гипотенуза

α - угол прилежащий к гипотенузе

Формула длины биссектрисы через катеты, ( L ):

Формула длины биссектрисы через гипотенузу и угол, ( L ):

2. Найти по формулам длину биссектрисы из острого угла на катет:

L - биссектриса, отрезок ME , исходящий из острого угла

a, b - катеты прямоугольного треугольника

с - гипотенуза

α , β - углы прилежащие к гипотенузе

Формулы длины биссектрисы через катет и угол, ( L ):

Формула длины биссектрисы через катет и гипотенузу, ( L ):

8. Длина биссектрисы равнобедренного треугольника

L - высота = биссектриса = медиана

a - одинаковые стороны треугольника

b - основание

α - равные углы при основании

β - угол образованный равными сторонами

Формулы высоты, биссектрисы и медианы, через сторону и угол, ( L ):

Формула высоты, биссектрисы и медианы, через стороны, ( L ):

9. Найти медиану биссектрису высоту равностороннего треугольника

Формула для вычисления высоты = биссектрисы = медианы.

В равностороннем треугольнике: все высоты, биссектрисы и медианы, равны. Точка их пересечения, является центром вписанной окружности.

L - высота=биссектриса=медиана

a - сторона треугольника

Формула длины высоты, биссектрисы и медианы равностороннего треугольника, ( L ):

10. Найти длину медианы треугольника по формулам

Медиана - отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам.

Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.

M - медиана, отрезок |AO|

c - сторона на которую ложится медиана

a, b - стороны треугольника

γ - угол CAB

Формула длины медианы через три стороны, ( M ):

Формула длины медианы через две стороны и угол между ними, ( M ):

11. Длина медианы прямоугольного треугольника

Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c , пополам.

Медиана в прямоугольном треугольнике ( M ), равна, радиусу описанной окружности ( R ).

Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.

СВОЙСТВА ТРЕУГОЛЬНИКА:

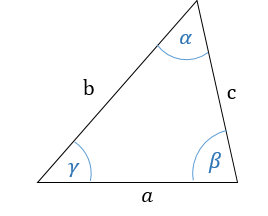
1. Сумма углов в треугольнике равна α + β + γ = 180°.

2. Против большей стороны находится больший угол; против меньшего угла находится меньшая сторона. Отсюда следует, что если:

Если это правило не выполняется — треугольник не существует.

4. Формулы площади треугольника:

1 (через высоту)

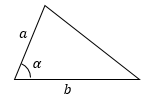
2 (через две стороны и синус угла между ними)

3 (формула Герона)

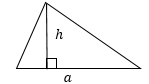
$S = \displaystyle\frac12 a h_a$

$S = \displaystyle\fracab\,\sin \alpha$

Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне.

Площадь треугольника равна половине произведения его сторон на синус угла между ними.

Площадь треугольника равна квадратному корню из произведения его полупериметра на разности полупериметра и каждой из его сторон.

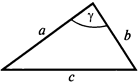
5. Теорема косинусов: квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

6. Теорема синусов: Отношения сторон треугольника к синусам противоположных им углов равны. Это отношение равно 2R, где R — радиус описанной окружности.

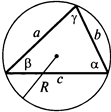
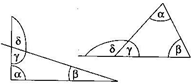
7. Внешний угол треугольника — δ, является смежным с одним из внутренних углов (сумма = 180°). Из этого следует, что внешний угол равен сумме двух внутренних, но не смежных с ним, углов треугольника (α + β = δ).

ВИДЫ ТРЕУГОЛЬНИКОВ:

остроугольными (если все его углы острые),
тупоугольными (если один из его углов тупой),
прямоугольными (если один из его углов прямой).

равнобедренным, если две его стороны равны;
равносторонним, если все три стороны равны;
разносторонним, если все его стороны разные.

ЭЛЕМЕНТЫ ТРЕУГОЛЬНИКА:

БИССЕКТРИСА

Биссектриса ― луч, который соединяет вершину треугольника с противоположной стороной, при этом разделяя угол на две равные части.

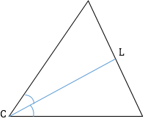
Свойства биссектрисы треугольника:

1. Все три биссектрисы треугольника пересекаются в одной точке. Эта точка — центр вписанной в треугольник окружности.

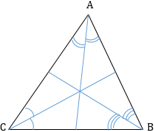
2. Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные двум другим сторонам.

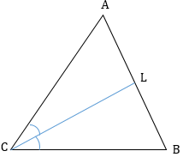
3. Формулы для биссектрисы треугольника. Если а и b — стороны треугольника, γ — угол между ними, l — биссектриса треугольника, проведённая из вершины этого угла, а а' и b' — отрезки, на которые биссектриса делит третью сторону треугольника, то

МЕДИАНА

Медиана ― отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

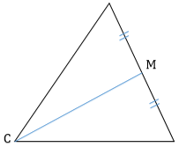
Свойства медианы треугольника:

1. Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и точкой пересечения делятся в отношении 2 к 1, считая от вершины.

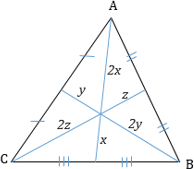
Медиана разбивает треугольник на два равновеликих (по площади) треугольника.
Треугольник делится тремя медианами на шесть равновеликих треугольников.
В прямоугольном треугольнике медиана, проведённая из вершины с прямым углом, равняется половине гипотенузы.
Формула для медианы треугольника. Если стороны треугольника a и b, m_c — медиана треугольника, проведённая к стороне c, то

ВЫСОТА

Высота — перпендикуляр, опущенный из вершины треугольника на противоположную сторону (точнее, на прямую, содержащую противоположную сторону).

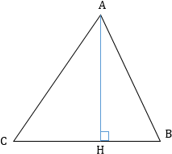
В зависимости от типа треугольника высота может содержаться:

внутри треугольника (для остроугольного треугольника),
совпадать с его стороной (являться катетом прямоугольного треугольника),
проходить вне треугольника (для тупоугольного треугольника).

Свойства высоты треугольника:

1. Все три высоты треугольника пересекаются в одной точке, которая называется ортоцентром.

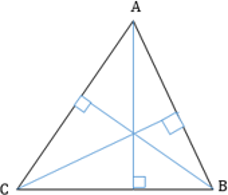
2. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.

3. Если в треугольнике две высоты равны, то треугольник — равнобедренный.

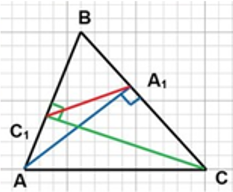
4. Если CC₁ и АА₁ — высоты треугольника АВС, то треугольник ВА₁С₁ подобен треугольнику АВС, причём коэффициент подобия равен cos B.

Сложные теоремы:

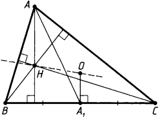
5. Если Н — точка пересечения высот треугольника AВС, а О — центр его описанной окружности, то отрезок АН вдвое больше расстояния от точки О до середины стороны ВС. То есть AH = 2OM.

6. Если Н — точка пересечения высот треугольника AВС, М — точка пересечения медиан треугольника AВС, а О — центр его описанной окружности, то точки О, H и М лежат на одной прямой (прямая Эйлера), причём точка М лежит на отрезке ОН и ОМ : МН = 1 : 2.

СРЕДИННЫЙ ПЕРПЕНДИКУЛЯР

Срединный перпендикуляр треугольника — прямая, перпендикулярная стороне треугольника и проходящая через его середину.

Все три срединных перпендикуляра треугольника пересекаются в одной точке, которая является центром описанной около треугольника окружности.

СРЕДНЯЯ ЛИНИЯ

Средняя линия треугольника — отрезок, соединяющий середины двух сторон этого треугольника

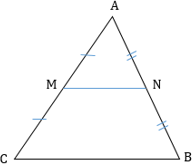
Свойства средней линии треугольника:

Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине:

В любом треугольнике три средних линии, при пересечении которых образуются 4 равных треугольника, подобных исходному с коэффициентом 1/2.

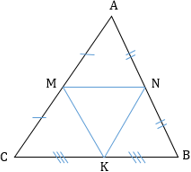
$\bigtriangleup AMN = \bigtriangleup NKB = \bigtriangleup NMK = \bigtriangleup MCK$

ПОДОБИЕ И РАВЕНСТВО ТРЕУГОЛЬНИКОВ

Подобные треугольники

Равные треугольники

Треугольники подобны, если их углы равны. В подобных фигурах сохраняется отношение между соответствующими сторонами и другими линейными величинами (высоты, медианы, биссектрисы и периметры):

$\displaystyle\frac=\frac=\frac=\frac$

Также сохраняется внутреннее отношение длин:

$\displaystyle\frac=\frac\ \ или\ \ \frac=\frac$

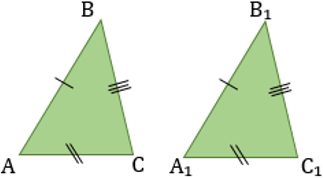
Два треугольника равны, если у них соответствующие стороны равны и соответствующие углы равны (треугольники равны, если их можно совместить наложением).

Признаки подобия треугольников:

1. По двум пропорциональным сторонам и углу между ними:

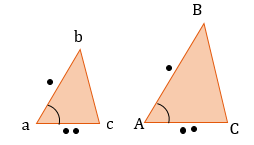
3. По двум равным углам (тогда и третьи тоже будут равны)

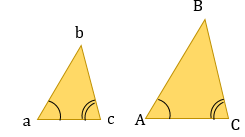
5. По трем пропорциональным сторонам:

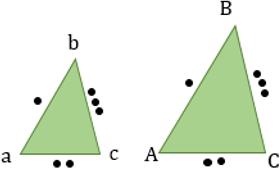
Признаки равенства треугольников:

1. По двум сторонам и углу между ними:

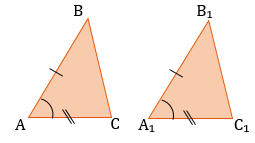
2. По стороне и двум прилежащим к ней углам.

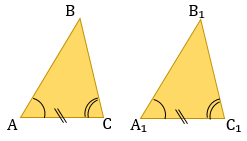
3. По трем сторонам.

ОСОБЫЕ ТРЕУГОЛЬНИКИ И ИХ СВОЙСТВА:

«Особенными», то есть обладающими какими — то дополнительными свойствами, считаются:

равнобедренный,
равносторонний
прямоугольный треугольники.

РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК

Равнобедренный треугольник ― это треугольник, у которого две стороны равны (АВ = АС).

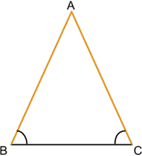
Равные стороны (АВ и АС) в таком треугольнике называются боковыми, а оставшаяся третья сторона (ВС) ― основанием.

Свойства равнобедренного треугольника:

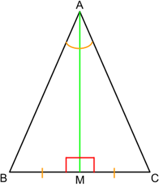
1. Углы при основании равны (∠АВС = ∠АСВ).

2. Медиана, проведённая к основанию, является биссектрисой и высотой. То есть она не только делит противолежащую сторону пополам (ВМ = МС), но и падает на неё под углом 90°, а кроме того делит угол, из которого выходит, пополам (∠ВАМ = ∠МАС).

Посмотрим на пример конкретной задачи. В равнобедренном треугольнике внешний угол равен 80°, необходимо найти все углы треугольника. Сразу возникает вопрос ― внешний угол при каком угле треугольника? Предположим, что это внешний угол при угле В (с нашего первого рисунка). Но в таком случае выходит, что сам ∠В = 100° (по сумме смежных углов). Значит, и ∠С = 100°, так как треугольник равнобедренный. Но тогда сумма только двух углов получается 200°, чего быть никак не может. Значит, речь идёт о внешнем угле при угле А треугольника. Тогда ∠А = 100°, а ∠В = ∠С = 40°.

РАВНОСТОРОННИЙ ТРЕУГОЛЬНИК

Равносторонний треугольник ― треугольник, у которого все три стороны равны

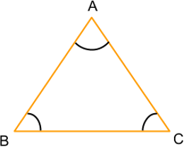
Свойства равностороннего треугольника:

1. Кроме равенства сторон в таком треугольнике равны и все углы (каждый из которых по 60° ― так как 180°/3 = 60°).

2. Медиана, проведённая из любого угла, будет являться биссектрисой и высотой (другими словами, равносторонний треугольник с любой стороны является равнобедренным).

1. Центры вписанной и описанной окружностей совпадают.

2. Формулы 2 и 3 для площади треугольника превращаются в одну формулу:

— Через синус (так как все стороны равны и каждый угол равен 60°):

— Формула Герона (так как все стороны равны):

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК

Прямоугольный треугольник ― треугольник, у которого один угол равен 90° (собственно, это и есть прямой угол, дающий название всему треугольнику). Сторона, лежащая против такого угла, называется гипотенузой (АВ), а две другие стороны ― катетами (АС и ВС).

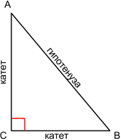
Свойства прямоугольного треугольника:

1. В любом прямоугольном треугольнике гипотенуза всегда больше катета (против большего угла лежит большая сторона, и наоборот).

2. Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов

Теорема, обратная теореме Пифагора: Если для сторон произвольного треугольника выполняется отношение АВ 2 = АС 2 + ВС 2 , то треугольник является прямоугольным.

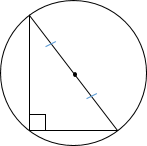
3. Центр описанной вокруг прямоугольного треугольника окружности всегда лежит на середине гипотенузы (доказательство: прямой ∠С становится вписанным, а против вписанного угла в 90° всегда лежит диаметр ― значит, гипотенуза является диаметром).

Высота, проведенная к гипотенузе, разбивает треугольник на два подобных прямоугольных треугольника, каждый из которых подобен исходному треугольнику: $\bigtriangleup ACH\sim\bigtriangleup HCB\sim\bigtriangleup ABC$

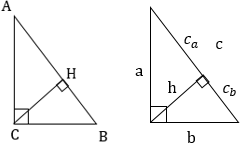
4. Высота, проведенная к гипотенузе, равна:

Произведению катетов, деленному на гипотенузу

Среднему геометрическому из произведений отрезков, на которые гипотенуза делится высотой

5. Медиана, проведенная к гипотенузе равна половине гипотенузы, то есть радиусу описанной около треугольника окружности.

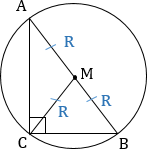
6. Формулы площади прямоугольного треугольника:

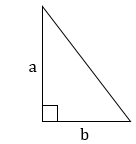
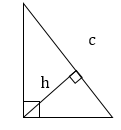
Площадь прямоугольного треугольника равна половине произведения его катетов.

Площадь прямоугольного треугольника равна половине произведения гипотенузы на опущенную к ней высоту.

Площадь прямоугольного треугольника равна половине произведения его катета, гипотенузы и синуса угла между ними.

ЗОЛОТОЙ И СЕРЕБРЯНЫЙ ТРЕУГОЛЬНИКИ:

Серебряный треугольник

— треугольник с углами 45°, 45° и 90° (разрубленный по диагонали квадрат)

Отношение сторон в серебряном треугольнике:

Типы треугольников

По величине углов

Остроугольный треугольник

Тупоугольный треугольник

Прямоугольный треугольник

По числу равных сторон

Разносторонний треугольник

Равнобедренный треугольник

Равносторонний (правильный) треугольник

Вершины, углы и стороны треугольника

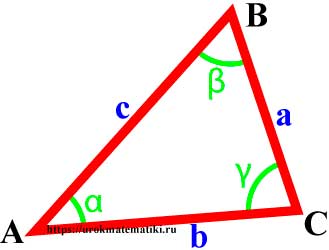
Свойства углов и сторон треугольника

Сумма углов треугольника равна 180°

В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы

если α > β , тогда a > b
если α = β , тогда a = b

Сумма длин двух любых сторон треугольника больше длины оставшейся стороны

Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов.

a sin α = b sin β = c sin γ

Теорема косинусов

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведение этих сторон на косинус угла между ними.

a 2 = b 2 + c 2 - 2 b c · cos α
b 2 = a 2 + c 2 - 2 a c · cos β
c 2 = a 2 + b 2 - 2 a b · cos γ

Теорема о проекциях

Для остроугольного треугольника:

a = b cos γ + c cos β
b = a cos γ + c cos α;
c = a cos β + b cos α;

Формулы для вычисления длин сторон треугольника

Формулы сторон через медианы

a = 2 3 2 m b 2 + m c 2 - m a 2

b = 2 3 2 m a 2 + m c 2 - m b 2

c = 2 3 2 m a 2 + m b 2 - m c 2

Медианы треугольника

Свойства медиан треугольника

Медианы треугольника пересекаются в одной точке. Точка пересечения медиан называется центроидом.

S ∆AOF = S ∆AOE = S ∆BOF = S ∆BOD = S ∆COD = S ∆COE

Формулы медиан треугольника

Формулы медиан треугольника через стороны

m a = 1 2 2 b 2 + 2 c 2 - a 2

m b = 1 2 2 a 2 + 2 c 2 - b 2

m c = 1 2 2 a 2 + 2 b 2 - c 2

Биссектрисы треугольника

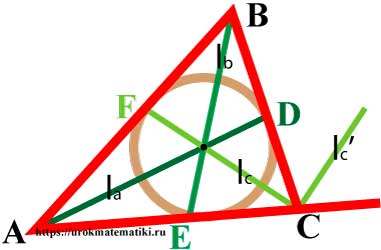
Свойства биссектрис треугольника

Биссектрисы треугольника пересекаются в одной точке, равноудаленной от трех сторон треугольника, - центре вписанной окружности.

Угол между l c и l c ' = 90°

Формулы биссектрис треугольника

Формулы биссектрис треугольника через стороны

l a = 2 b c p p - a b + c

l b = 2 a c p p - b a + c

l c = 2 a b p p - c a + b

Формулы биссектрис треугольника через две стороны и угол

l a = 2 b c cos α 2 b + c

l b = 2 a c cos β 2 a + c

l c = 2 a b cos γ 2 a + b

Высоты треугольника

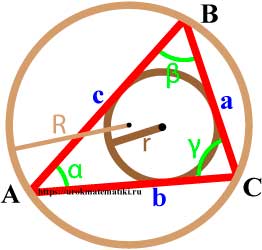
В зависимости от типа треугольника высота может содержаться:

Свойства высот треугольника

Высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника.

Формулы высот треугольника

Формулы высот треугольника через сторону и угол

h a = b sin γ = c sin β

h b = c sin α = a sin γ

h c = a sin β = b sin α

Формулы высот треугольника через сторону и площадь

Формулы высот треугольника через две стороны и радиус описанной окружности

Окружность вписанная в треугольник

Окружность называется вписанной в треугольник, если она касается всех трех его сторон.

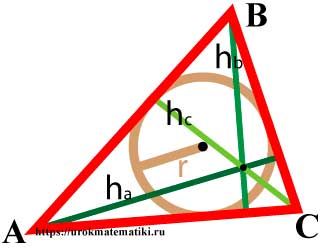
Свойства окружности вписанной в треугольник

Центр вписанной в треугольник окружности лежит на пересечении биссектрис внутренних углов треугольника.
В любой треугольник можно вписать окружность, и только одну.

Формулы радиуса окружности вписанной в треугольник

Радиус вписанной в треугольник окружности равен отношению площади треугольника к его полупериметру

Радиус вписанной в треугольник окружности через три стороны

Формулы высот треугольника через две стороны и радиус описанной окружности

Окружность описанная вокруг треугольника

Окружность называется описанной вокруг треугольника, если она содержит все вершины треугльника.

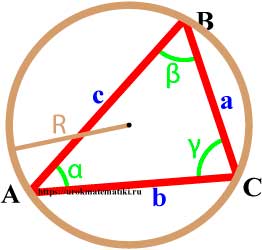
Свойства окружности описанной вокруг треугольника

Центр описанной вокруг треугольника окружности лежит на пересечении серединных перпендикуляров к его сторонам.
Вокруг любого треугольника можно описать окружность, и только одну.

Свойства углов

Центр описанной окружности лежит внутри остроугольного треугольника, снаружи тупоугольнго треугольника, на середине гипотенузы прямоугольного треугольника.

Формулы радиуса окружности описанной вокруг треугольника

Радиус описанной окружности через три стороны и площадь

Радиус описанной окружности через площадь и три угла

Радиус описанной окружности через сторону и противоположный угол (теорема синусов)

Связь между вписанной и описанной окружностями треугольника

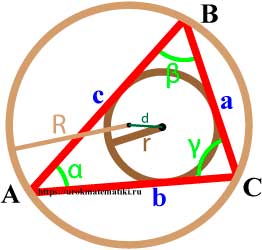
Формулы радиуса окружности описанной вокруг треугольника

d 2 = R 2 - 2 R r

Радиус описанной окружности через площадь и три угла

Средняя линия треугольника

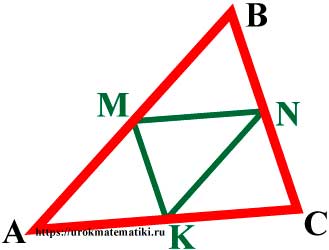
Свойства средней линии треугольника

Любой треугольник имеет три средних линии.
Средняя линия треугольника параллельна основанию и равна его половине.
MN = 1 2 AC ; KN = 1 2 AB ; KM = 1 2 BC

Признаки

Периметр треугольника

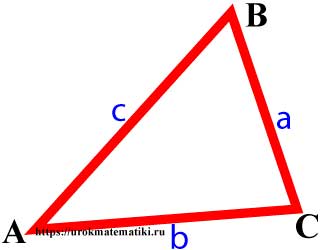
Периметр треугольника ∆ABC равен сумме длин его сторон.

Формулы площади треугольника

Формула площади треугольника по стороне и высоте

Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты.

S = 1 2 a · h a ,
S = 1 2 b · h b ,
S = 1 2 c · h c ,

Формула площади треугольника по трем сторонам

Формула Герона формула для вычисления площади треугольника S по длинам его сторон a, b, c .

S = p p - a p - b p - c ,

Формула площади треугольника по двум сторонам и углу между ними

Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.

S = 1 2 a · b · sin γ ,
S = 1 2 b · c · sin α ,
S = 1 2 a · c · sin β ,

Формула площади треугольника по трем сторонам и радиусу описанной окружности

Формула площади треугольника по трем сторонам и радиусу вписанной окружности

Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

Равенство треугольников

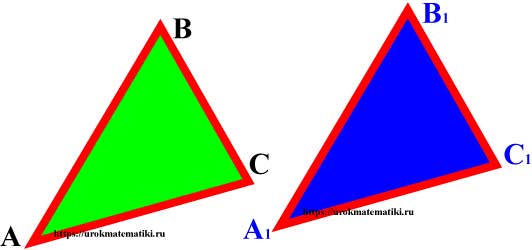
Определение

Если два треугольника АВС и А₁В₁С₁ можно совместить наложением, то они равны.

Свойства

У равных треугольников равны и их соответствующие элементы. (В равных треугольниках против равных сторон лежат равные углы, против равных углов лежат равные стороны).

Признаки равенства треугольников

По двум сторонам и углу между ними

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

По стороне и двум прилежащим углам

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

По трем сторонам

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Подобие треугольников

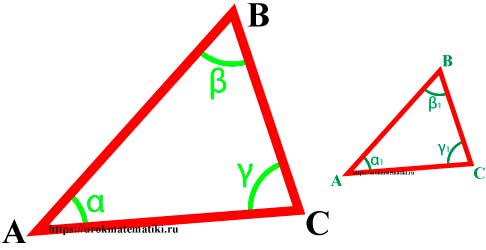
Определение

∆MNK => α = α 1 , β = β 1 , γ = γ 1 и AB MN = BC NK = AC MK = k

Признаки подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
Если две стороны одного треугольника пропорциональны двум сторонам другого, а углы, между этими сторонами, равны, то такие треугольники подобны.

Свойства

Площади подобных треугольников относятся как квадрат коэффициента подобия:

S ∆АВС S ∆MNK = k 2

Прямоугольные треугольники

Свойства прямоугольного треугольника

Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы (гипотенуза в два раза длиннее катета, лежащего против угла в 30°).

Докажем, что BC=2AC.
Приложим к треугольнику ABC равный ему треугольник ABD , как показано на рисунке.
Получим треугольник BCD, в котором ∡B = ∡D = 60° , поэтому DC = BC. Но DC = 2AC. Следовательно, BC = 2AC.

Справедливо и обратное суждение: Если катет прямоугольного треугольника равен половине гипотенузы (или гипотенуза в два раза длиннее катета), то угол, лежащий против этого катета, равен 30°.

Признаки равенства прямоугольных треугольников

Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.

Свойства

Площади подобных треугольников относятся как квадрат коэффициента подобия:

Читайте также: