Метод якоби в экселе
Обновлено: 07.07.2024
В данной статье мы расскажем общие сведения об итерационных методах решения СЛАУ, познакомим с методом Зейделя и Якоби, а также приведем примеры решения систем линейных уравнений при помощи данных методов.
Общие сведения об итерационных методах или методе простой итерации
Метод итерации — это численный и приближенный метод решения СЛАУ.
Суть: нахождение по приближённому значению величины следующего приближения, которое является более точным. Метод позволяет получить значения корней системы с заданной точностью в виде предела последовательности некоторых векторов (итерационный процесс). Характер сходимости и сам факт сходимости метода зависит от выбора начального приближения корня x 0 .
Рассмотрим систему A x = b .
Чтобы применить итерационный метод, необходимо привести систему к эквивалентному виду x = B x + d . Затем выбираем начальное приближение к решению СЛАУ x ( 0 ) = ( x 1 0 , x 2 0 , . . . x m 0 ) и находим последовательность приближений к корню.
Для сходимости итерационного процесса является достаточным заданное условие В < 1 . Окончание итерации зависит от того, какой итерационный метод применили.
Метод Якоби
Метод Якоби — один из наиболее простых методов приведения системы матрицы к виду, удобному для итерации: из 1-го уравнения матрицы выражаем неизвестное x 1 , из 2-го выражаем неизвестное x 2 и т.д.
Результатом служит матрица В , в которой на главной диагонали находятся нулевые элементы, а все остальные вычисляются по формуле:
b i j = - a i j / a i i , i , j = 1 , 2 . . . , n
Элементы (компоненты) вектора d вычисляются по следующей формуле:
d i = b i / a i i , i = 1 , 2 , . . . , n
Расчетная формула метода простой итерации:
x ( n + 1 ) = B x ( x ) + d
Матричная запись (координатная):
x i ( n + 1 ) = b i 1 x n 1 + b i 2 x ( n ) 2 + . . . + b
Критерий окончания в методе Якоби:
x ( n + 1 ) - x ( n ) < ε 1 , где ε 1 = 1 - B B ε
В случае если B < 1 / 2 , то можно применить более простой критерий окончания итераций:
x ( n + 1 ) - x ( n ) < ε
Решить СЛАУ методом Якоби:
10 x 1 + x 2 - x 3 = 11 x 1 + 10 x 2 - x 3 = 10 - x 1 + x 2 + 10 x 3 = 10
Необходимо решить систему с показателем точности ε = 10 - 3 .
Приводим СЛАУ к удобному виду для итерации:
x 1 = - 0 , 1 x 2 + 0 , 1 x 3 + 1 , 1 x 2 = - 0 , 1 x 1 + 0 , 1 x 3 + 1 x 3 = 0 , 1 x 1 - 0 , 1 x 2 + 1
Выбираем начальное приближение, например: x ( 0 ) = 1 , 1 1 1 — вектор правой части.
В таком случае, первая итерация имеет следующий внешний вид:
x 1 ( 1 ) = - 0 , 1 × 1 + 0 , 1 × 1 + 1 , 1 = 1 , 1 x 2 ( 1 ) = - 0 , 1 × 1 , 1 + 0 , 1 + 1 = 0 , 99 x 3 ( 1 ) = 0 , 1 × 1 , 1 - 0 , 1 × 1 + 1 = 1 , 01
Аналогичным способом вычисляются приближения к решению:
x ( 2 ) = 1 , 102 0 , 991 1 , 011 , x ( 3 ) = 1 , 102 0 , 9909 1 , 0111 , x ( 4 ) = 1 , 10202 0 , 99091 1 , 01111
Находим норму матрицы В , для этого используем норму B ∞ .
Поскольку сумма модулей элементов в каждой строке равна 0,2, то B ∞ = 0 , 2 < 1 / 2 , поэтому можно вычислить критерий окончания итерации:
x ( n + 1 ) - x ( n ) < ε
Далее вычисляем нормы разности векторов:
x ( 3 ) - x ( 2 ) ∞ = 0 , 002 , x ( 4 ) - x ( 3 ) ∞ = 0 , 00002 .
Поскольку x ( 4 ) - x ( 3 ) ∞ < ε , то можно считать, что мы достигли заданной точности на 4-ой итерации.
x 1 = 1 , 102 ; x 2 = 0 , 991 ; x 3 = 1 ,01 1 .
Метод Зейделя
Метод Зейделя — метод является модификацией метода Якоби.
Суть: при вычислении очередного ( n + 1 ) - г о приближения к неизвестному x i при i > 1 используют уже найденные ( n + 1 ) - е приближения к неизвестным x 1 , x 2 , . . . , x i — 1 , а не n - о е приближение, как в методе Якоби.
x i ( n + 1 ) = b i 1 x 1 ( n + 1 ) + b i 2 x 2 ( n + 1 ) + . . . + b i , i - 1 x i - 2 ( n + 1 ) + b i , i + 1 x i + 1 ( n ) +
+ . . . + b i m x m ( n ) + d i
За условия сходимости и критерий окончания итераций можно принять такие же значения, как и в методе Якоби.
Решить СЛАУ методом Зейделя. Пусть матрица системы уравнений А — симметричная и положительно определенная. Следовательно, если выбрать начальное приближение, метод Зейделя сойдется. Дополнительных условий на малость нормы некоторой матрицы не накладывается.
Решим 3 системы уравнений:
2 x 1 + x 2 = 3 x 1 - 2 x 2 = 1 , x 1 + 2 x 2 = 3 2 x 1 - x 2 = 1 , 2 x 1 - 0 , 5 x 2 = 3 2 x 1 + 0 , 5 x 2 = 1
Приведем системы к удобному для итерации виду:
x 1 ( n + 1 ) = - 0 , 5 x 2 ( n ) + 1 , 5 x 2 ( n + 1 ) = 0 , 5 x 1 ( n + 1 ) + 0 , 5 , x 1 ( n + 1 ) = - 2 x 2 ( n ) + 3 x 2 ( n + 1 ) = 2 x 1 ( n + 1 ) - 1 , 2 x 1 - 0 , 5 x 2 = 3 2 x 1 + 0 , 5 x 2 = 1 .
Отличительная особенность, условие сходимости выполнено только для первой системы:
Вычисляем 3 первых приближения к каждому решению:
1-ая система: x ( 0 ) = 1 , 5 - 0 , 5 , x ( 1 ) = 1 , 75 0 , 375 , x ( 2 ) = 1 , 3125 0 , 1563 , x ( 3 ) = 1 , 4219 0 , 2109
Решение: x 1 = 1 , 4 , x 2 = 0 , 2 . Итерационный процесс сходится.
2-ая система: x ( 0 ) = 3 - 1 , x ( 1 ) = 5 9 , x ( 2 ) = - 15 - 31 , x ( 3 ) = 65 129
Итерационный процесс разошелся.
Решение: x 1 = 1 , x 2 = 2
3-я система: x ( 0 ) = 1 , 5 2 , x ( 1 ) = 2 - 6 , x ( 2 ) = 0 2 , x ( 3 ) = 0 2
Итерационный процесс зациклился.
Решение: x 1 = 1 , x 1 = 2
Метод простой итерации
Если А — симметричная и положительно определенная, то СЛАУ приводят к эквивалентному виду:
x = x - τ ( A x - b ) , τ - итерационный параметр.
Расчетная формула имеет следующий внешний вид:
x ( n + 1 ) = x ( n ) - τ ( A x n - b ) .
Здесь B = E - τ A и параметр τ > 0 выбирают таким образом, чтобы по возможности сделать максимальной величину B 2 .
Пусть λ m i n и λ m a x - максимальные и минимальные собственные значения матрицы А .
τ = 2 / ( λ m i n + λ m a x ) - оптимальный выбор параметра. В этом случае B 2 принимает минимальное значение, которое равняется ( λ m i n + λ m a x ) / ( λ m i n - λ m a x ) .
Рассмотрим достаточные условия сходимости итерационной последовательности n>.
Практически, для применения метода итерации систему линейных уравнений удобно "погрузить" в одну из трёх следующих метрик:
(3.4)
Для того, чтобы отображение F, заданное в метрическом пространстве соотношениями (3.2), было сжимающим, достаточно выполнение одного из следующих условий:
а) в пространстве с метрикой ρ1: , т. е. максимальная из сумм модулей коэффициентов в правой части системы (3.2), взятых по строкам, должна быть меньше единицы.
б) в пространстве с метрикой ρ2: , т. е. максимальная из сумм модулей коэффициентов в правой части системы (3.2), взятых по столбцам, должна быть меньше единицы.
в) в пространстве с метрикой ρ3: , т. е. сумма квадратов при неизвестных в правой части системы (3.2) должна быть меньше единицы
Пример . Вычислить два приближения методом простой итерации. Оценить погрешность второго приближения. В качестве начального приближения выбрать x 0 =(0; 0; 0).
Так как диагональные элементы системы являются преобладающими, то приведем систему к нормальному виду:
Последовательные приближения будем искать по формулам:
При большом числе неизвестных схема метода Гаусса, дающая точное решение, становится весьма сложной. В этом случае для решения СЛАУ иногда удобнее пользоваться методом простой итерации.
Метод итераций для системы уравнений в Excel
На листе Excel организуется таблица в три зоны: первая зона состоит из одного столбца (номер итерации), вторая зона определяет переменные x , третья зона под вычисления точности epsilon .Во второй зоне по итерационной схеме организуется расчет переменных x (в примере для случая трех переменных):
Итерация №1: =$F$2/$B$2-C6*$C$2/$B$2-D6*$D$2/$B$2;=$F$3/$C$3-B6*$B$3/$C$3-D6*$D$3/$C$3;=$F$4/$D$4-B6*$B$4/$D$4-C6*$C$4/$D$4
Итерация №2: =$F$2/$B$2-C7*$C$2/$B$2-D7*$D$2/$B$2;=$F$3/$C$3-B7*$B$3/$C$3-D7*$D$3/$C$3;=$F$4/$D$4-B7*$B$4/$D$4-C7*$C$4/$D$4
Пример 3.1.Найти решение системы линейных алгебраических уравнений (3.1) методом Якоби.
Итерационные методы можно использовать для заданной системы, т.к. выполняется условие «преобладания диагональных коэффициентов», что обеспечивает сходимость этих методов.
Расчетная схема метода Якоби приведена на рис (3.1).
Приведите систему(3.1). к нормальному виду:
или в матричной форме
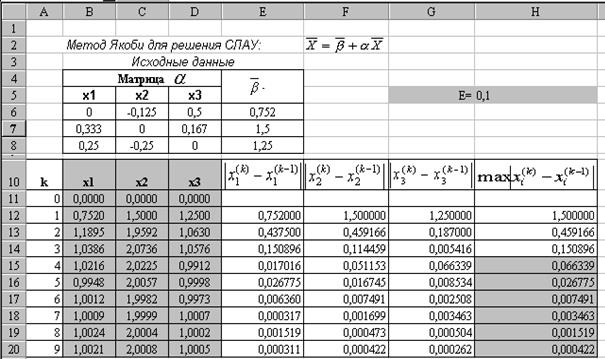 |
Рис.3.1.
Для определения количества итераций, необходимое для достижения заданной точности e,и приближенного решения системы полезно в столбце Н установить Условный формат. Результат такого форматирования виден на рис.3.1. Ячейки столбца Н, значения которых удовлетворяют условию (3.4) тонированы.
Анализируя результаты, принимаем за приближенное решение исходной системы с заданной точностью e=0,1 четвертую итерацию,
Изменяя значение eв ячейке Н5 можно получить новое приближенное решение исходной системы с новой точностью.
Проанализируйте сходимость итерационного процесса, построив графики изменения каждой компоненты решения СЛАУ в зависимости от номера итерации.
Для этого выделите блок ячеек А10:D20 и, используя Мастер диаграмм, постройте графики, отражающие сходимость итерационного процесса, рис.3.2.
Аналогично решается система линейных алгебраических уравнений методом Зейделя.
Лабораторная работа №4
Тема. Численные методы решения линейных обыкновенных дифференциальных уравнений с краевыми условиями. Метод конечных разностей
Задание.Решить краевую задачу методом конечных разностей, построив два приближения (две итерации) с шагом h и с шагом h/2.
Проанализировать полученные результаты. Варианты заданий приведены в приложении 4.
Порядок выполнения работы
1. Постройте вручную конечноразностную аппроксимацию краевой задачи (конечноразностную СЛАУ) с шагом h, заданным вариантом.
2. Используя метод конечных разностей, сформируйте в Excelсистему линейных алгебраических конечно-разностных уравнений для шага h разбивки отрезка [a, b]. Запишите эту СЛАУ на рабочем листе книги Excel. Расчетная схема приведена на рис.4.1.
3. Полученную СЛАУ решите методом прогонки.
4. Проверьте правильность решения СЛАУ с помощью надстройки Excel Поиск решения.
5. Уменьшите шаг сетки в 2 раза и еще раз решите задачу. Результаты представьте в графическом виде.
6. Сравните полученные результаты. Сделайте вывод о необходимости продолжения или о прекращении счета.
Решение краевой задачи с использованием электронных таблиц Microsoft Excel.
Пример 4.1.Методом конечных разностей найти решение краевой задачи ,y(1)=1, y ’ (2)=0,5 на отрезке xÎ[1, 2] с шагом h=0,2 и с шагом h=0,1. Сравнить полученные результаты и сделать вывод о необходимости продолжения или о прекращении счета.
Расчетная схема для шага h=0,2 приведена на рис.4.1.
Полученное решение (сеточную функцию) Y, Х в столбце L и B можно принять за первую итерацию (первое приближение) исходной задачи.
 |
Для нахождения второй итерации сделайте сетку вдвое гуще (n=10, шаг h=0,1) и повторите приведенный выше алгоритм.
Это можно проделать на том же или на другом листе книги Excel. Решение (второе приближение) приведено на рис.4.2.
Сравните полученные приближенные решения. Для наглядности можно построить графики этих двух приближений (двух сеточных функций), рис.4.3.
Порядок построения графиков приближенных решений краевой задачи
1. Постройте график решения задачи для разностной сетки с шагом h=0,2 (n=5).
2. Активизируйте уже построенный график и выберите команду меню Диаграмма\Добавить данные
3. В окне Новые данные укажите данные xi, yi для разностной сетки с шагом h/2 (n=10).
4. В окне Специальная вставка установите флажки в полях:
Ø категории(значение оси х) в первом столбце.

Как видно из приведенных данных, два приближенных решения краевой задачи (две сеточные функции) отличаются друг от друга не более, чем на 5%. Поэтому за приближенное решение исходной задачи принимаем вторую итерацию, т.е.
Для решения систем линейных алгебраических уравнений (СЛАУ) большой размерности, а также систем, имеющих разреженные матрицы, применение точных методов (например, метод Гаусса) не является целесообразным, так как сказывается ограниченность разрядной сетки и накапливается погрешность округления.
Система с разреженной матрицей получается, например, при составлении системы уравнений теплового баланса технологической схемы или же при численном расчете потенциалов из дифференциального уравнения Гельмгольца на равномерной сетке. Есть и другие примеры, которые приводят нас к необходимости решать СЛАУ с разряженной матрицей.
Рассмотрим здесь простейший метод решения линейных систем - метод простых итераций.
Так как я не люблю сложные теоретические усложнения, то начну с простого примера системы с тремя неизвестными.
Допустим, у вас есть следующая система уравнений:
Здесь x1, x2, x3 - неизвестные, а a[i][j] и b[i] - известные постоянные Здесь x1, x2, x3 - неизвестные, а a[i][j] и b[i] - известные постоянныеВ матричном виде эту систему можно было бы записать так:
Выразим из 1-го уравнения системы первую неизвестную x1
Выразим из 2-го уравнения системы вторую неизвестную x2
Выразим из 3-го уравнения системы третью неизвестную x3
Заметим, что элементы, лежащие на главное диагонали матрицы не должны быть нулевые. Ну а если такое случается, то надо переставлять местами уравнения, так, чтобы выполнялось условие неравенства нулю диагональных элементов.
Итак, все эти три уравнения мы можем записать общей формулой, если перейдем к индексам: первый индекс будет пробегать по строкам, а второй по столбцам. В нашей теории нумерация начинается с 1.
Обратите внимание, что в скобках, где находится сумма произведений, не встречается элемента с совпадающими индексами (тот а[k][k] который лежит на диагонали), поэтому при суммировании мы должны его пропустить.
В принципе, этот пропуск можно реализовать конструкцией continue при программировании алгоритма. Но если вам это не нравится, то общую формулу суммы можно переписать в другом виде:
Таким образом мы тоже можем пропустить ненужный элемент, не использую дополнительных конструкций if при программировании. Таким образом мы тоже можем пропустить ненужный элемент, не использую дополнительных конструкций if при программировании.Постараюсь сделать схему решения еще более понятной для программирования:
Важные уточнения:
columns - количество столбцов
k - текущий корень системы, совпадает с номером строки матрицы
i - номер столбца, индекс, по которому проводится суммирование
x[i] - старые корни, полученные на предыдущей итерации
x[k] - новый корень, которые считается на базе корней, полученных на предыдущей итерации
Иногда, в книгах по численным методам еще используется верхний индекс (чаще всего в скобках, чтоб не спутали со степенью), чтобы разграничить где решение на новой итерации, а где решение на предыдущей итерации.
У нас получается рекуррентная формула:
На мой взгляд, не нужно особо обращать внимание на верхние индексы, показывающие где новая итерация, а где старая. Так как начинающих это только сбивает с толку. В реальной программе это будет перезапись одной и той же переменной, БЕЗ как либо верхних индексов.
Приведу очень простой пример, почему на практике не нужны загромождения верхними индексами для рекуррентной формулы :
Теперь опять вернемся к нашей задаче. Итерационный процесс можно запустить до бесконечности и далее. Шучу, нельзя. Компилятор быстро спустит вас с небес на землю! Но когда останавливаться? Теория говорит нам, что можно остановиться при достижении необходимой точности.
Точность часто обозначается буквой экспилон ε , ну а в программировании взяли за правило обозначать eps ( сокращение от epsilon ), так как греческими буквами нам нельзя пользоваться при написании названий переменных.
Для остановки и проверки точности, а также завершения вычислений на основе вычисления расстояния между соседними элементами в последовательности итераций можно воспользоваться Евклидовой метрикой .
В этом случае, условие завершения вычислений следующее:
Евклидова метрика для определения достижения необходимой точности Евклидова метрика для определения достижения необходимой точностиПо сути, это что-то вроде относительной погрешности, учитывающий все решения, а именно среднеквадратичные отклонения, чтобы исключить влияние знака. Потому что при сложении абсолютных разниц у нас могла произойти иллюзия достижения необходимой точности и иллюзия маленького разброса, если бы одна разница была бы большой со знаком "+", а другая разница примерно такой же большой, но со знаком "-". Они бы просто друг друга аннигилировали и дали бы нам ложный результат. Именно поэтому используются квадраты отклонений, а потом уже накладывается корень.
Для того, чтобы мы могли считать Евклидову метрику на каждой итерации, нам необходимо сохранять вектор решения на предыдущей итерации. То есть считая новый набор корней на новой итерации, мы должны сохранить старый набор корней на предыдущей итерации, чтобы было потом с чем сравнивать.
На практике же, я бы посоветовал помимо погрешности ограничивать выполнения цикла каким-либо предельным количеством итераций. Например, чтобы максимальное число итераций было 100
500 . Для адекватной сходимости этого достаточно за глаза. Так как, если метод сходится, то система достигает нужной точности примерно за 20-50 итераций (чаще всего, если точность eps = 0.0001 ).
Уже совсем другое дело, если решение расходится. Именно тогда вас спасает ограничение по числу итераций, чтобы не войти в бесконечный цикл.
Следует отметить, что скорость сходимости итерационного процесса выше для матриц, у которых элементы главной диагонали велики по сравнению с внедиагональными элементами. В связи с этим, перед началом численного решения задачи желательно преобразовать систему уравнений так, чтобы преобладали диагональные элементы.
Также, чтобы запустить рекуррентную формулу и начать любой метод итераций, нам нужно начальное приближение корней. Можно взять любое, но в разумных пределах. К примеру, можно использовать столбец свободных коэффициентов в матричном представлении системы. Или просто обнулить начальное приближение. Или везде поставить единицы. Если метод будет сходиться, то он в любом случае придет к корням с нужным приближением.
Порядок решения СЛАУ методом Якоби такой:
● Приведение системы уравнений к виду, в котором на каждой строчке выражено какое-либо неизвестное значение системы.
● Произвольный выбор нулевого решения, в качестве него можно взять вектор-столбец свободных членов.
● Производим подстановку произвольного нулевого решения в систему уравнений, полученную под пунктом 1.
● Осуществление дополнительных итераций, для каждой из которых используется решение, полученное на предыдущем этапе.
Читайте также:

