Множества с которыми работает компьютер может быть бесконечным

Обновлено: 04.07.2024

Что такое «множество», мы понимаем интуитивно. В этом смысле это понятие первично, так же как «точка» или «плоскость».

Создатель теории множеств Г.Кантор описывал множество как «многое, мыслимое нами как единое».

Приведём примеры множеств:

Множество людей в салоне самолёта

Множество деревьев в парке

Множество планет Солнечной системы

Множество электронов в атоме

Множество натуральных чисел

Множество «синих-синих презелёных красных шаров»

Конечное, бесконечное и пустое множества

Людей в салоне самолёта легко посчитать, это множество конечно.

С деревьями в парке, планетами и электронами – сложней. Скорее всего, мы не сможем назвать точное количество элементов этих множеств в данный момент времени. Однако, и эти множества конечны.

Натуральное число – это идеальный объект, абстракция. Множество натуральных чисел бесконечно. Как оказалось, человек может оперировать и абстракциями, и бесконечностями.

Можно себе представить даже то, «чего на свете вообще не может быть». Поскольку таких объектов нет, их множество будет пустым. Пустое множество является частью любого другого множества.

Конечные множества

Бесконечные множества

Пустые множества

Помидоры на грядке

Числа (натуральные, рациональные, действительные и т.д.)

Количество рациональных чисел на отрезке [0;1]

Полосатые летающие слоны

Все точки пересечения двух параллельных прямых на плоскости

Способы задания множеств

1) Перечисление – в списке задаются все элементы множества.

Множество всех континентов Земли:

Множество букв слова «математика»:

Множество натуральных чисел меньших 5:

2) Характеристическое свойство – указывается особенность элементов множества.

A = $\$ - множество всех действительных положительных x

B = $\$ - множество всех натуральных n, кратных 5

C = $\$ – множество всех действительных точек координатной плоскости (x,y), расстояние от которых до начала координат не больше 1 (круг с центром в начале координат, радиусом 1).

D = – множество всех материков планеты Земля

3) Графическое изображение – визуальное моделирование с помощью различных диаграмм (круги Эйлера, интервалы, графики и т.п.)

Подмножества

Множество A называют подмножеством множества B (A $\subseteq$ B), если всякий элемент множества A также является элементом множества B:

$$ A \subseteq B \iff (a \in \Bbb A \Rightarrow a \in \Bbb B) $$

Говорят, что B содержит A, или B покрывает A.

Пустое множество является подмножеством любого множества.

Знак $\subseteq$ является аналогом $\ge$, т.е. «нестрогим» неравенством. Это значит, что множества A и B могут и совпадать (любое множество является подмножеством самого себя).

Между множествами можно также ввести отношение «строгое подмножество», $A \subset B$, в котором B заведомо «шире» множества A (аналог строгого неравенства $\lt$).

Примеры подмножеств:

Множество людей является подмножеством приматов, живущих на Земле.

Множество натуральных чисел меньших 5 является подмножеством натуральных чисел меньших $10: A = \, B = \, A \subseteq B$

Множество квадратов является подмножеством прямоугольников.

Множество полосатых летающих слонов – как пустое множество - является подмножеством чего угодно: приматов, чисел, прямоугольников. Что удобно для размышлений о смысле всего.

Множество всех подмножеств данного множества A называют булеаном или степенью множества A.

Булеан конечного множества из n элементов содержит $2^n$ элементов:

Примеры

Пример 1. Запишите данное множество с помощью перечисления элементов:

Задано множество целых чисел, квадрат которых меньше 5. Перечисляем:

Задано множество целых чисел, модуль которых не больше 3. Перечисляем:

Задано множество рациональных чисел, являющихся корнями уравнения

(x-1)(2x+5) = 0. Перечисляем:

Задано множество натуральных чисел, входящих в полуинтервал $9 \lt n \le 12$.

Пример 2. Запишите данное множество с помощью характеристического свойства:

а) Множество всех натуральных чисел меньше 10

б) Множество всех действительных чисел, кроме 0

в) Множество всех точек с целыми координатами, принадлежащих прямой y = 2x+1

г) Множество всех целых решений уравнения $x^3+x^2+4 = 0$

Пример 3. Изобразите на графике в координатной плоскости данное множество:

Задано конечное множество точек, которое можно представить перечислением:

Задано бесконечное множество точек, принадлежащих данной гиперболе $y = \frac$ в данном интервале $-4 \le x \le -1$. На графике:

Пример 4. Укажите и запишите с помощью перечисления одно из непустых конечных подмножеств для данного множества:

Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.

Информатика. Учебник для 9 класса (по учебнику К. Ю. Полякова, Е.А. Еремина, базовый уровень)

§12. Множества и логика.

Множества

Ключевые слова:

Множество — некоторый набор элементов, каждый из которых отличается от остальных. Множество может состоять из конечного числа элементов (например, множество букв русского алфавита), бесконечного числа элементов (например, множество натуральных чисел) или вообще быть пустым (например, множество слонов, живущих на Северном полюсе). Пустое множество обозначается символом ∅. Множества, с которыми работает компьютер, не могут быть бесконечными, потому что его память конечна.

Чтобы определить множество, мы можем перечислить все его элементы. Например, множество, состоящее из Васи, Пети и Коли, можно записать так: .

Запишите в виде перечисления элементов:

а) множество натуральных чисел на отрезке [-5; 5];
б) множество чётных однозначных чисел;
в) множество целых чисел, делящихся на 4, на отрезке [0; 22];
г) множество простых чисел на отрезке [5; 20].

Запишите (словами или в символьном виде) условие, которое определяет множество:

Хотя множество — это математическое понятие, с множествами мы имеем дело каждый раз, когда обращаемся к поисковой системе в Интернете: ведь нас интересует множество страниц, на которых есть нужная нам информация. Задать такое множество перечислением элементов невозможно: во-первых, мы не знаем адресов этих страниц; во-вторых, их очень много. Поэтому для того, чтобы задать нужное нам множество, требуется написать поисковый запрос — логическое выражение, которое его определяет.

Диаграммы Эйлера-Венна

Множества удобно изображать графически, в виде диаграмм. Их называют диаграммами Эйлера—Венна в честь авторов этой идеи — математика Леонарда Эйлера и логика Джона Венна. На такой диаграмме каждому множеству соответствует какая-то область (круг, прямоугольник и др.) — рис. 2.34. Все элементы внутри этой области принадлежат множеству, все элементы вне области — не принадлежат.

Рис. 2.34

Вы уже знаете, что множество можно задать условием (логическим выражением), которое выполняется для всех элементов множества и не выполняется для всех элементов, не входящих в него. Дальше для сокращения записи мы будем вместо слов «множество, для которого выполняется условие А» писать просто «множество А». Тогда множество «НЕ А» на диаграмме — это все точки за границами круга (рис. 2.35).

Рис. 2.35

Такое множество называется дополнением множества А до универсального множества U, включающего все элементы некоторого класса. Например, если мы рассматриваем только целые числа и А — это множество чётных целых чисел, то А — множество нечётных целых чисел.

Можно считать, что дополнение А — это «разность» между универсальным множеством U и множеством А, т. е. все элементы из U, которые не входят в А.

Для каждого из следующих множеств выберите универсальное множество и запишите дополнение А:

На диаграмме можно изображать несколько множеств, каждому из них соответствует своя область (круг). Круги на диаграмме могут пересекаться. Элементы, расположенные в общей части кругов А и В, — это пересечение множеств А и В. Для этих элементов выполняется как условие А, так и условие В, т. е. выполняется условие А и В (А • В) — рис. 2.36.

Рис. 2.36

Если круги не пересекаются (множества не содержат общих элементов), их пересечение — это пустое множество ∅.

Для пары множеств определите пересечение А • В:

Элементы, входящие хотя бы в одно из множеств: в А или в В, образуют новое множество, которое называется объединением множеств А и В. Для всех элементов этого множества выполняется условие А или В (А + В) — рис. 2.37.

Рис. 2.37

Для пары множеств определите объединение А + В:

Подобные диаграммы можно нарисовать для любого логического выражения, ведь каждое из них определяет некоторое множество. Например, возьмём выражение А + В. Оно равно 0 только при А = 1 и В = 0, поэтому на диаграмме незакрашенной останется только область, которая входит в круг А и не входит в круг В (рис. 2.38).

Рис. 2.38

В тетради постройте диаграммы для логических выражений:

а) А + B;
б) А • B + А • В;
в) А • B + А • B.

Диаграмма для трёх переменных содержит три круга, каждый из которых (в общем случае) пересекается с двумя другими (рис. 2.39).

Рис. 2.39

Для удобства на рис. 2.39 области пронумерованы. Запишем, для примера, логическое выражение для области 3. Эта область находится внутри кругов А и B (следовательно, выражения А и B истинны), но вне круга С, поэтому выражение С ложно. Получается условие А и B и (не С), или, в других обозначениях, А • B • C.

Запишите в тетради логические выражения для остальных областей на рис. 2.39.

Для того чтобы найти выражение для объединения двух или нескольких областей, надо сложить (используя логическое сложение — операцию ИЛИ) выражения для всех составляющих. Например, выражение для объединения областей 3 и 4 на рис. 2.39 имеет вид:

3 + 4:А • В • C + А • В • C.

Вместе с тем точки в этих областях отличаются от других тем, что они входят в область Б и не входят в область С. Поэтому справедлива более простая формула:

Это означает, что логические выражения в некоторых случаях можно упростить.

Количество элементов во множестве

Предположим, что множество А содержит 10 элементов, множество B — 15 элементов, а их пересечение (множество А • B) — два элемента. Как определить, сколько элементов содержится во множестве А + В?

Попробуем рассмотреть задачу в общем виде и вывести формулу для её решения. Обозначим через N_x число элементов в области X. Далее операцию И будет обозначать символом &, а операцию ИЛИ — символом | (именно эти символы используются в поисковых запросах в Интернете).

Построим диаграмму с двумя областями — А и В. Эти области могут быть разделены (рис. 2.40, а) или пересекаться (рис. 2.40, б).

Рис. 2.40

В первом случае (рис. 2.40, а), когда области не пересекаются, получаем очевидную формулу:

Во втором случае (рис. 2.40, б) в сумму N_A + N_B общие элементы (элементы множества N_A&B) входят дважды. Поэтому, чтобы получить количество элементов в объединении множеств, нужно из этой суммы вычесть число общих элементов:

Эта формула, которую называют формулой включений и исключений, справедлива и для рис. 2.40, а, где N_A&B = 0.

Используя формулу (*), постройте выражения для вычисления N_A и N_A&B

Рыбаки в посёлке ловят только лещей и судаков. 25 рыбаков ловят лещей, 12 рыбаков — судаков, причём 5 рыбаков ловят и лещей, и судаков. Сколько всего рыбаков в посёлке? Выполните формализацию задачи и решите её.

У дяди Вани живёт 30 животных: овцы и кролики. Все кролики белые, а у овец разный цвет шерсти. Известно, что у дяди Вани живёт 18 овец и 25 животных с белой шерстью. Сколько белых овец у дяди Вани? Выполните формализацию задачи и решите её.

В физико-математическом классе 27 учеников. Среди них нет таких, которые не программируют и не ходят в турпоходы. Известно, что 20 человек ходят в турпоходы, среди них 5 программистов. Сколько в классе программистов? Выполните формализацию задачи и решите её.

Сложные запросы в поисковых системах

Для решения задач, в которых используются множества, например множества страниц, полученных от поисковой системы в ответ на какой-то запрос, удобно применять диаграммы Эйлера-Венна.

Задача 1. Известно количество страниц, которые находит поисковый сервер по следующим запросам (здесь символ «&» обозначает операцию И, а «|» — операцию ИЛИ):

собаки | кошки 770

собаки & кошки 100

Сколько страниц будет найдено по запросу собаки?

Введём два множества: А — множество страниц, где есть слово «собаки», В — множество страниц со словом «кошки». По формуле, которая получена в предыдущем пункте, получаем:

Известно количество страниц, которые находит поисковый сервер по следующим запросам:

лилия & незабудка 100

лилия | незабудка 450

Сколько страниц найдёт этот сервер по запросу лилия?

Известно количество страниц, которые находит поисковый сервер по следующим запросам:

кашалот | енот 450

Сколько страниц найдет этот сервер по запросу

Известно количество страниц, которые находит поисковый сервер по следующим запросам:

Франция & Италия 80

Сколько страниц найдёт этот сервер по запросу

Рассмотрим теперь более сложную задачу с тремя областями.

Задача 2. Известно количество страниц, которые находит поисковый сервер по следующим запросам:

собаки & лемуры 320

кошки & лемуры 280

(кошки | собаки) & лемуры 430

Сколько страниц будет найдено по запросу

кошки & собаки & лемуры?

Заметим, что во всех запросах есть часть & лемуры. Это означает, что область поиска во всех случаях ограничена страницами, на которых встречается слово «лемуры».

Обозначим буквами С, К и Л области (группы страниц), содержащие ключевые слова «собаки», «кошки» и «лемуры» соответственно. Нас интересует только область, выделенная фоном на рис. 2.41, а.

Рис. 2.41

Эта область образована в результате пересечения двух областей (рис. 2.41, б):

А = собаки & лемуры

В = кошки & лемуры

Поэтому задачу можно свести к задаче с двумя областями.

Известно количество страниц, которые находит поисковый сервер по следующим запросам:

Сколько страниц будет выдано по запросу А & В?

Используя формулу включений и исключений, полученную в предыдущем пункте, находим:

Известно количество страниц, которые находит поисковый сервер по следующим запросам:

берёза & сирень 220

берёза & сирень & арбуз 30

сирень & (берёза | арбуз) 340

Сколько страниц найдёт этот сервер по запросу

Известно количество страниц, которые находит поисковый сервер по следующим запросам:

яхта & диван 270

диван & пирог 350

яхта & диван & пирог 80

Сколько страниц найдёт этот сервер по запросу

(пирог | яхта) & диван?

Задачу с тремя областями не всегда удаётся свести к более простой задаче с двумя областями. Серьёзным упрощением может стать то, что какие-то два множества не имеют общих элементов.

Если два множества не имеют общих элементов, что можно сказать об их изображении на диаграмме Эйлера-Венна?

Задача 3. Известно количество страниц, которые находит поисковый сервер по следующим запросам:

кошки | собаки 450

кошки & лемуры 40

собаки & лемуры 50

Сколько страниц найдёт этот сервер по запросу

(кошки | собаки) & лемуры?

Здесь часть & лемуры встречается не во всех запросах, поэтому свести задачу к задаче с двумя областями не удаётся. Используя те же обозначения, что и в задаче 2, построим диаграмму с тремя переменными и выделим интересующую область, которая соответствует запросу (кошки I собаки) & лемуры.

На рисунке 2.42 эта область выделена фоном.

Рис. 2.42

В общем виде задача с тремя областями очень сложна. Попробуем найти какое-нибудь упрощающее условие. Например, выделим три условия:

кошки | собаки 450

Это означает, что область кошки | собаки равна сумме областей кошки и собаки, т. е. эти области не пересекаются! Таким образом, в нашем случае диаграмма выглядит так (рис. 2.43).

Рис. 2.43

Размеры областей 1 (собаки & лемуры) и 2 (кошки & лемуры) нам известны, они составляют соответственно 40 и 50 страниц, поэтому по запросу

(кошки | собаки) & лемуры

поисковый сервер найдёт 40 + 50 = 90 страниц.

Известно количество страниц, которые находит поисковый сервер по следующим запросам:

крабы | солнце 450

солнце & лето 20

Сколько страниц найдёт этот сервер по запросу

крабы | солнце | лето?

Выводы

• Множество — это набор неповторяющихся элементов.
• Множество может состоять из конечного числа элементов, бесконечного числа элементов или быть пустым. Множества, с которыми работает компьютер, не могут быть бесконечными, потому что его память конечна.
• Чтобы определить множество, можно перечислить все его элементы или задать условие, которое определяет элементы множества. Для всех элементов множества это условие должно быть истинным, для элементов, не входящих во множество, — ложным.
• Дополнение множества А до универсального множества U, включающего все элементы некоторого класса, — это все элементы из U, которые не входят в А.
• Пересечение двух множеств — это множество, составленное из элементов, входящих в оба исходных множества.
• Объединение двух множеств — это множество, составленное из элементов, которые входят хотя бы в одно из этих множеств.
• Для наглядного изображения множеств используют диаграммы Эйлера-Венна, на которых каждое множество обозначается кругом или другой фигурой.
• На диаграмме Эйлера-Венна дополнение множества А — это все точки за пределами области А; пересечение множеств А и В — это общая часть областей А и В, а объединение множеств А и В — это все точки, входящие в область А или в область В.
• Количество элементов в объединении двух множеств вычисляется по формуле включений и исключений:

где N_A и N_B — число элементов соответственно в множествах А и В, a N_A&B — число их общих элементов.

Самым первым видом данных, с которыми начали работать компьютеры, были числа. ЭВМ первого поколения могли производить только математические расчёты (вычисления).

Из курса информатики основной школы вы помните, что компьютеры работают с целыми и вещественными числами. Их представление в памяти осуществляется разными способами.

Во многих задачах, решаемых на компьютере, обрабатываются целочисленные данные. Прежде всего, это задачи экономического характера, при решении которых данными служат количества акций, сотрудников, деталей, транспортных средств и др. Целые числа используются для обозначения даты и времени, для нумерации различных объектов: элементов массивов, записей в базах данных, машинных адресов и т. д. По своей природе множество целых чисел дискретно, т. к. состоит из отдельных элементов.

И хотя любое целое число можно рассматривать как вещественное, но с нулевой дробной частью, предусмотрены специальные способы представления целых чисел. Это обеспечивает: эффективное расходование памяти, повышение быстродействия, повышение точности вычислений за счёт введения операции деления нацело с остатком.

Для компьютерного представления целых чисел используется несколько различных способов, отличающихся друг от друга количеством разрядов (под целые числа обычно отводится 8, 16, 32 или 64 разряда) и наличием или отсутствием знакового разряда.

Беззнаковое представление можно использовать только для неотрицательных целых чисел.

Для получения компьютерного представления беззнакового целого числа в n-разрядной ячейке памяти достаточно перевести его в двоичную систему счисления и, при необходимости, дополнить полученный результат слева нулями до n-разрядов.

Например, десятичные числа 130 и 39 в восьмиразрядном представлении будут иметь вид:

Понятно, что существуют ограничения на числа, которые могут быть записаны в n-разрядную ячейку памяти. Максимальное значение целого неотрицательного числа достигается в случае, когда во всех разрядах ячейки хранятся единицы. Для n-разрядного представления оно будет равно 2 n - 1. Минимальное число соответствует n нулям, хранящимся в n разрядах памяти, и равно нулю. Далее приведены диапазоны значений для беззнаковых целых n-разрядных чисел:

При знаковом представлении целых чисел старший разряд ячейки отводится под знак (0 — для положительных, 1 — для отрицательных чисел), а остальные разряды — под цифры числа.

Представление числа в привычной для человека форме «знак-величина», при которой старший разряд ячейки отводится под знак, а остальные разряды — под цифры числа, называется прямым кодом.

Например, прямые коды чисел 48 и -52 для восьмиразрядной ячейки равны:

Минимальное отрицательное число, которое можно записать в знаковом представлении в n разрядах, равно 2 n-1 . Максимальное положительное число, которое можно записать в знаковом представлении в п разрядах, равно 2 n-1 - 1. Ниже приведены диапазоны значений для знаковых представлений целых чисел в ячейках с различной разрядностью:

В математике множество целых чисел бесконечно.

Компьютер работает с ограниченным множеством целых чисел.

Прямой код положительного числа отличается от прямого кода равного по абсолютной величине отрицательного числа только содержимым знакового разряда.

В прямом коде числа можно хранить, но выполнение арифметических операций над числами в прямом коде затруднено — оно требует более сложной архитектуры центрального процессора, «умеющего» выполнять не только сложение, но и вычитание, а также «знающего» особый алгоритм обработки не имеющего «веса» знакового разряда. Этих трудностей позволяет избежать использование дополнительного кода.

Чтобы понять сущность дополнительного кода, рассмотрим работу реверсивного счётчика, последовательность показаний которого можно представить в виде замкнутого кольца из чисел (рис. 3.5).

При возрастании показаний счётчика до максимального, например до 999, следующими его состояниями должны быть 1000, 1001, 1002 и т. д. Но для изображения старшей единицы в счётчике не хватает разряда, происходит переполнение разрядной сетки. Поэтому мы увидим 000, 001, 002 и т. д.

При убывании показаний счётчика после состояния 000 будут идти 999, 998, 997 и т. д. Но после достижения нуля последовательное вычитание единицы должно давать -1, -2, -3 и т. д.

Будем рассматривать числа 999, 998, 997 как коды чисел -1, -2, -3 и проверим на их примере соотношение: у + (-у) = 0:

001 + 999 = 1000;
002 + 998 = 1000;
003 + 997 = 1000.

С учётом того что единица переполнения теряется, мы, сложив число и код противоположного ему числа, получаем ноль!

Вот ещё несколько примеров:

5 - 2 = 5 + [-2] = 5 + 998 = 1003;
7 - 5 = 7 + [-5] = 7 + 995 = 1002.

Для устранения неоднозначности в кольце будем считать половину состояний (0-499) кодами нуля и положительных чисел, а оставшуюся половину (500-999) — кодами отрицательных чисел.

Таким образом, дополнительный код положительного числа совпадает с этим числом, а для отрицательного числа он равен дополнению его величины до числа q n , возникающего при переполнении разрядной сетки. Здесь q — основание системы счисления, n — число разрядов в разрядной сетке.

Рассмотрим алгоритм получения дополнительного n-разрядного кода отрицательного числа:

1) модуль числа представить прямым кодом в n двоичных разрядах;

2) значения всех разрядов инвертировать (все нули заменить единицами, а единицы — нулями);

3) к полученному представлению, рассматриваемому как n-разрядное неотрицательное двоичное число, прибавить единицу.

Пример 1. Найдём 16-разрядный дополнительный код отрицательного числа -2017₁₀.

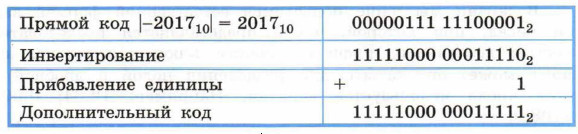
Использование дополнительного кода позволяет свести операцию вычитания чисел к операции поразрядного сложения кодов этих чисел.

Пример 2. Как известно, 48 - 2017 = -1969.

Выполним эту операцию в 16-разрядных машинных кодах.

Нам потребуются прямой код числа 48 и дополнительный код числа -2017.

Рассмотрим полученный результат. Это отрицательное число (об этом говорит 1 в знаковом разряде), представленное в дополнительном коде. Перейдём к прямому коду модуля соответствующего числа, по которому сможем восстановить десятичное представление результата.

Прямой код можно получить из дополнительного кода, если применить к нему операцию инвертирования и прибавить единицу.

В математике множество вещественных чисел непрерывно, бесконечно и не ограничено.

Попробуйте обосновать это утверждение.

Вещественные числа записываются в естественной или в экспоненциальной форме.

В жизни мы чаще пользуемся естественной формой записи чисел, при которой: число представляется последовательностью десятичных цифр со знаком плюс или минус, знак плюс может опускаться, для разделения целой и дробной частей числа используется запятая. Например: 12,34; 0,0056; -708,9.

В экспоненциальной форме вещественное число а представляется как а = ± m • q p , где m — мантисса числа, q — основание системы счисления, р — порядок числа.

Например, длину некоторого отрезка, равного 47,8 см, можно записать так:

1) 478 • 1 0-1 см;
2) 47,8 • 10 0 см;
3) 4,78 • 10 1 см;
4) 0,478 • 10 2 см;
5) 0,000478 • 10 5 см.

Такое многообразие вариантов записи в экспоненциальной форме одного и того же числа не всегда удобно. Для однозначного представления вещественных чисел в компьютере используется нормализованная форма.

Нормализованная запись отличного от нуля вещественного числа 1 — это запись вида а = ± m • q p , где р — целое число (положительное, отрицательное или ноль), m — дробь, целая часть которой содержит одну значащую (ненулевую) цифру, т. е. 1 ≤ m < q.

1 Стандарт IEEE 754.

Примеры нормализации чисел:

Диапазон вещественных чисел в памяти компьютера очень широк, но, тем не менее, ограничен. Множество вещественных чисел, которые могут быть представлены в компьютере, конечно.

Поясним это на примере калькулятора, который производит вычисления в десятичной системе счисления. Пусть это будет калькулятор с десятью знакоместами на дисплее:

6 знакомест отводится под мантиссу (одно знакоместо отводится под знак мантиссы, четыре — под цифры мантиссы, одно — под точку, разделяющую целую и дробную части мантиссы);
одно знакоместо отводится под символ «Е»;
три знакоместа отводятся под порядок (одно — под знак порядка, два — под цифры порядка).

У калькуляторов первая значащая цифра, с которой и начинается мантисса, изображается перед точкой.

Число 12,34 в таком калькуляторе будет представлено как +1.234Е+01.

Число 12,35 будет представлено как +1.235Е+01.

Как известно, между числами 12,34 и 12,35 находится бесконечное множество вещественных чисел, например: 12,341; 12,3412; 12,34123 и т. д.

Каждое из этих чисел в нашем калькуляторе будет представлено как + 1.234Е+01. Для последних разрядов у нас просто не хватает знакомест! Аналогичная ситуация имеет место и в компьютерном представлении вещественных чисел, независимо от того, ячейки какой разрядности там использованы.

Получается, что точно мы можем представить в компьютере лишь некоторую конечную часть множества вещественных чисел, а остальные числа — лишь приближённо.

Таким образом, множество вещественных чисел, представляемых в компьютере, дискретно, конечно и ограничено.

Самое главное

В математике множество целых чисел дискретно, бесконечно и не ограничено.

Для компьютерного представления целых чисел используется несколько различных способов, отличающихся друг от друга количеством разрядов (8, 16, 32 или 64 разряда) и наличием или отсутствием знакового разряда. В любом случае компьютерное представление целых чисел дискретно, конечно и ограничено.

В математике множество вещественных чисел непрерывно, бесконечно и не ограничено.

Для компьютерного представления вещественных чисел используется нормализованная запись вещественного числа а = ± m • q p , где q — основание системы счисления, р — целое число (положительное, отрицательное или ноль), m — дробь, целая часть которой содержит одну значащую (ненулевую) цифру, т. е. 1 ≤ m < q.

Компьютерное представление вещественных чисел дискретно, конечно и ограничено.

Учебник Информатика 10 класс Углубленный уровень Поляков Еремин часть 1 - 2014-2015-2016-2017 год: Читать онлайн (cкачать в формате PDF) - Щелкни! Пояснение: Для скачивания книги (с Гугл Диска), нажми сверху справа - СТРЕЛКА В ПРЯМОУГОЛЬНИКЕ . Затем в новом окне сверху справа - СТРЕЛКА ВНИЗ . Для чтения - просто листай колесиком страницы вверх и вниз.

>(В>С))ЦВ> А) ^(С> В)). Чему равно В, если А = 27 и С = 25? Логические основы компьютеров Данное сложное высказывание состоит из трёх простых: (А = В\ (А>В)^С), (В> А)^(С>В). Они связаны операцией *И», т. е. должны быть истинными одновременно. Из условия (А = В) = 1 сразу следует, что АфВ. Далее можно использовать несколько способов решения. Способ 1 (решение «по частям»). Предположим, что А> В, тогда из второго условия получаем 1 (В > С). Это выражение может быть истинно тогда и только тогда, когда (В>С) = 1, поэтому имеем А> В>С. Этому условию соответствует только число 26. Одно решение найдено. Теперь проверим вариант А (В>С), это выражение истинно при любом В. Проверяем третье условие; получаем 1->(С>В) = 1; это выражение может быть истинно тогда и только тогда, когда С>В, и тут мы получили противоречие, потому что нет такого числа В, для которого С> В> А. Таким образом, правильный ответ — 26, других решений нет. Способ 2. Раскрываем импликацию через операции «ИЛИ» и «НЕ»: (А>В)-»(В>С) = (А>В) + (В>С) = (В> А) + (В>0, (В> А)^(С>В) = (В> А) + (С>В) = (В и и 27) +(В >25) = (В >25), (В 25 и В В) + (А —»В); б) (А ->В) (А -4В); в) (А В)(А 4-В); г) (А 4-В)-» (А В); д) (А -^В) (А-ьС) (А •С); е) (А ^ В) (А ^ С); ж) А В(В 4-С); з) (А ^ В) -»(А -» С); и) (А С). Логические операции 3. Символом F обозначено одно из указанных ниже логических выражений от трёх аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F. Какие из этих выражений могут соответствовать F? X у Z F 1 1 1 1 1 1 0 1 1 0 0 1 и) X + Y + Z; б) X + Y+Z; B)X + Y + Z; r)X + Y-Z. 4. Для предыдущего задания определите, сколько различных логических функций соответствует заданной частичной таблице истинности. 5. Задано 5 строк таблицы истинности некоторого логического выражения с тремя переменными. Сколько различных логических функций ей соответствуют? 6. Символом F обозначено одно из указанных ниже логических выражений от трёх аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F. Какие из этих выражений могут соответствовать F? X у Z F 0 1 0 0 1 1 0 1 0 1 1 0 а) X + Y + Z; б) XYZ; в) X + Y + Z; r)X + YZ. 7. Символом F обозначено одно из указанных ниже логических выражений от трёх аргументов: X, У, Z. Дан фрагмент таблицы истинности выражения F. Какие из этих выражений могут соответствовать F? X у Z F 1 0 0 1 0 0 0 1 1 1 1 0 а) X -+’(Y + Z); б) X Y Z; B)X + Y + Z; г) X + Y + Z. Логические основы компьютеров 8. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F. Какие из этих выражений могут соответствовать F7 X у Z F 1 0 0 1 0 0 0 0 1 1 1 0 &)XYZ\ б) X ^(y + Z); b)X + Y + Z\ v)Y -^ Z b) (x + Y)-^Z b)X+ 2) —^ (X > 3) для X = 1, 2, 3, 4. 11. Определите значение логического выражения ((X (Х (Х 3)н-(Х (Х 2 Х-25)-^(Х>7)дляХ = 4, 5, 6, 7. 15. Найдите все целые значения X, при которых логическое выражение (X > 2) (X > 5) ложно. 16. Найдите все целые значения X, при которых логическое выражение ((X > 0) -I- (X > 4)) —»(X >4) ложно. Логические операции §19 17. Автопилот может работать, если исправен главный бортовой компьютер или два вспомогательных. Выполните формализацию и запишите логические формулы для высказываний «Автопилот работоспособен» и «Автопилот неработоспособен*. 18. Каково наибольшее целое положительное число X, при котором истинно утверждение: <Х(Х + 3) >Х2 + 9) -> (Х(Х + 2) Х-1-5)? 20. Каково наибольшее целое положительное число X, при котором ложно утверждение: (X (X + 6) -I- 9 > 0) ^ (Х2 > 45)? 21. Каково наибольшее целое положительное число X, при котором истинно утверждение: (Х2 -1 > 100) (X(X -1) 65)? 23. Известно, что для чисел А, В и С истинно утверждение ((С (2С >А)) ((А (А >2С)). Чему равно А, если С = 10 и В = 22? ■ Логические основы компьютеров §20 Диаграммы Венна Выражения, зависящие от небольшого количества переменных (обычно не более четырёх), удобно изображать в виде диаграмм, которые называют диаграммами Венна или кругами Эйлера. На такой диаграмме каждой переменной соответствует круг, внутри которого она равна единице, а вне его — нулю. Круги могут пересекаться. Области, в которых рассматриваемое логическое выражение истинно, закрашиваются каким-либо цветом. На рисунке 3.14 приведены диаграммы для простейших операций с одной и двумя переменными. Серым цветом залиты области, где рассматриваемое выражение равно единице. Рис. 3.14 Такие диаграммы часто используются при работе с множествами: операция «И» соответствует пересечению двух множеств, а «ИЛИ» — объединению. Для трёх переменных диаграмма будет немного сложнее. Для каждой из областей показанной на рис. 3.15 диаграммы запишем логические выражения. А В С 2: А-Ъ-С 3: АВС 4: АВС Ъ: А-ВС 6: А-ВС 7-.А-В-С 8: А-ВС Рис. 3.15 Диаграммы Венна §20 Для того чтобы найти выражение для объединения двух или нескольких областей, надо применить логическое сложение (операцию «ИЛИ») к выражениям для всех составляющих. Например, выражение для объединения областей 3 и 4 имеет вид 3 + 4: А В С + А В С. Вместе с тем если не обращать внимания на область А, то можно заметить, что справедлива формула 3 -f-4: В С. Это означает, что логические выражения в некоторых случаях можно упростить. Как это делается, вы узнаете в следующем параграфе. Диаграммы удобно применять для решения задач, в которых используются множества, например множества страниц, полученных от поисковой системы в ответ на какой-то запрос. Рассмотрим следующую задачу. Задача 1. Известно количество страниц, которые находит поисковый сервер по следующим запросам (здесь символ «&» обозначает операцию «И», а «|» — операцию «ИЛИ»): собаки I кошки кошки собаки & кошки 770 550 100 Сколько страниц будет выдано по запросу собаки? Сначала попробуем рассмотреть задачу в общем виде и вывести формулу для её решения. Построим диаграмму с двумя областями А и В. Эти области могут быть разделены (рис. 3.16, а) или пересекаться (рис. 3.16, б). А&.В Рис. 3.16 Логические основы компьютеров Обозначим через число страниц, которые выдаются по запросу X. В первом случае, когда области не пересекаются, получаем очевидную формулу:

^а '^^в- значит, что коли- чество страниц, полученных lio запросу А \ В, будет равно сумме результатов по отдельным запросам. Во втором случае (рис. 3.16, б) сумма +Ng дважды включает общую область, т. е. результат запроса А & В. Поэтому формула изменяется: . В

^А&В • Это более общий случай, справедливый и для рис. 3.16, а, где ^А&в нашей задачи (область А — собаки, область В — кошки) получаем: =^А\в

А + АВ = (а + А)(а + В) = ^ + В. Таким образом, мы вывели формулу, которая позволяет заменить импликацию через операции «НЕ» и «ИЛИ». Способ 2. Если в таблице истинности нулей меньше, чем единиц, удобнее сначала найти формулу для обратного выражения, X, а потом применить операцию «НЕ». В данном случае выражение равно нулю в единственной строке, при А = 1 и Б = 0, только в этой строке ^ = 1, поэтому, используя предыдущий способ, получаем Х = А В. Теперь остаётся применить операцию «НЕ» и закон де Моргана: Х = АВ=А+В. Рассмотрим более сложный пример, когда выражение зависит от трёх переменных. В этом случае в таблице истинности будет 8 строк (рис. 3.20). А В с X 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 0 1 0 1 1 1 1 0 0 1 1 1 1 АВС АВС АВС АВС АВС АВС Рис. 3.20 Отметим все строки, где Х = 1, и для каждой из них построим выражение, истинное только для этой комбинации переменных (см. рис. 3.20). Теперь выполним логическое сложение: Х = 'а Ъ с + ^ В С +

А В С + ^ В С + А В С + А В С. 7-^8 Логические основы компьютеров Упрощение этого выражения даёт: Х = АВ(С + С) +АВ(С + С) +А-С-(Б + В) = = АВ + А-В + А-С = А(В + В) + АС = = А +АС = (А +А)-(А+С) = А+С. Используя второй способ, получаем: х = аЪс + авс = ас(в + в) = ас. Тогда Х = А С=А+С. В данном случае второй способ оказался проще, потому что в столбце X таблицы истинности меньше нулей, чем единиц. Способ 3. При небольшом количестве нулей можно использовать ещё один метод. Попробуем применить операцию «НЕ» к исходному выражению для X, без предварительного упрощения: Х = АВС+АВС. Применяя закон де Моргана, получим: Х = (АВС)-(АВС). Используя закон де Моргана для обеих скобок, находим: Х=(а + В+С)(а+Ъ + С). Заметим, что выражение в каждой скобке ложно только для одной комбинации исходных данных, при которых Х = 0. Таким образом, третий способ заключается в том, чтобы для каждой строки в таблице истинности, где выражение равно О, построить логическую сумму, в которую переменные, равные в этой строке единице, входят с инверсией, а равные нулю — без инверсии. Выражение для X — это произведение полученных сумм. В нашем примере выражение упрощается с помощью распределительного закона для «И» и закона исключённого третьего: Х=(А + В+С)(А+В + С) = (А+С) + ВВ = А+С. Неудивительно, что мы получили тот же ответ, что и раньше. Иногда при упрощении выражений может потребоваться искусственный приём, который сначала вроде бы усложняет запись, но затем позволяет получить более простую форму. Например, рассмотрим выражение Х = ^В +

АС + ЪС. Синтез логических выражений §22 Учитывая, что В + В=1, можно представить второе слагаемое в виде: _ _____ _ _ _ _ А С = А (В + В) С = А В С +А В С. Тогда получаем: X =

А - В С + ^ Ъ С + Ъ С =

Понятие “Множество” в математике и информатике играет очень важную роль. В математике существует целая теория множеств.

В курсе А.В. Горячева “Информатика в играх и задачах”, рассчитанного на учащихся начальной школы, тема “Множества” рассматривается и во 2 классе, и в 3 и в 4 классах. Естественно, что эта тема прорабатывается с детьми не один урок, а задания постепенно усложняются.

1. На первом уроке по теме “Множества” важно сразу же дать четкие определения тех терминов, которые потом будут использоваться в самых различных заданиях. Урок основан на использовании презентации (см. Приложение 1).

Множество произошло от слова “много”. Но в математике понятие “множество” используется более широко.

Множество может объединять любое количество предметов, чисел, существ. Каждый предмет множества называется элементом множества.

Множество, которое не содержит элементов, называется пустым.

Множество может иметь подмножества.

Множества могут пересекаться, не пересекаться, объединяться.

Равными называются множества, состоящие из одинакового числа одинаковых элементов.

(Желательно, чтобы эти определения были записаны учащимися в тетрадь, чтобы потом они могли к ним вернуться.)

Эти определения необходимо закрепить на простейших примерах, например: множество животных имеет несколько подмножеств: рыбы, птицы, звери, насекомые – и они не пересекаются. Если же мы возьмем множество морских животных, то оно будет пересекаться с множеством птиц и множеством зверей (приводятся несколько примеров). В качестве пустого множества можно дать такой пример: в яркий солнечный день на небе нет облаков, поэтому в этот день множество облаков (такое множество естественно существует) – пустое, а в другой день оно уже не будет пустым. Этот пример используется в тетради А.В. Горячева “Информатика в играх и задачах” 3 класс, часть 2. Можно привести и другие примеры, когда какое-то множество в конкретной ситуации будет пустым.

Также для удобства выполнения различных заданий необходимо ввести систему обозначения множеств (геометрические фигуры), подчеркнув, что это только условное обозначение, но оно очень удобно. Элементы множеств обозначаются точками.

Для закрепления понятия “элементы множества” учащимся предлагается следующее задание 1 (приложение 2) (его можно давать как домашнее задание, которое вклеивается в тетрадь).

2. Далее вводятся понятия, связанные с использованием логических связок в названиях множеств.

В названиях множеств и высказываниях могут употребляться логические связки: “и”, “не”, “или” и их комбинация: “не … и”, “не … или”. “не … и не …”

Если в названии множества есть связка “не”, то его элементы находятся за пределами фигуры, обозначающей это множество.

Если в названии множества есть связка “и”, то его элементы находятся на пересечении фигур, обозначающих множества.

Если в названии множества есть связка “или”, то это означает, что его элементы находятся в нескольких фигурах.

Эти схемы также необходимо закрепить с учащимися на разных примерах, включенных в задания в тетради (курс Горячева для начальной школы), а также на тех, где они сами приводят примеры различных множеств. Для закрепления понятий пересечения и объединения множеств учащимся предлагается дополнительное задание 2.

3. На следующем(их) уроке(ах) следует продолжить подробный разбор заданий, например, включив задания на пересечение трех множеств. (Желательно также, чтобы эти схемы были зарисованы учащимися в тетрадях).

При пересечении 2-х множеств образуется IV области: 2 области без пересечения, одна область пересечения множеств и одна область, лежащая за пределами выделенных множеств.

При пересечении 3-х множеств образуется VIII областей: 3 области без пересечения, 4 области пересечения множеств и 1 область, лежащая за пределами выделенных множеств.

При пересечении двух множеств закрашивается вся область пересечения этих множеств. При объединении двух множеств закрашиваются оба множества. При пересечении трех множеств закрашивается общая часть всех трех множеств. При отрицании всех трех множеств закрашивается область, не включающая в себя сами множества.

Данные схемы сделаны для задания, когда надо распределить слова, в состав которых входят буквы “С”, “Т” и “О”. Набор слов должен включать слова только с “Т”, только с “С”, только с “О”, а также одновременно с двумя и тремя буквами. Два-три слова должны быть без букв “С”, “Т”, “О”. (Например: рельсы, купе, проводник, скорость, колесо, электровоз, тамбур, вагон, сумка, место, шпалы, поезд, машинист, билет, состав, дверь, станция).

В курсе информатики А.В. Горячева в тетради 2 класса есть аналогичное задание на множества “Круглые”, “Желтые”, “Шары”.

Закрепление теоретического материала должно сопровождаться решением задач. Простейшие задачи, например, “Про коз и коров”, “Фиалки и подруги”, “Газеты и журналы” могут быть использованы даже во 2 классе (см. приложение 4). Для более сильных учеников и для более старших классов, соответственно, можно подобрать задачи нужного уровня, а можно также использовать какие-то задачи и для проведения конкурсов, КВНов, школьных олимпиад, недели математики и информатики. Подобные задачи удобно решать, используя схему множеств и обозначая элементы просто точками (если числа малые) или указывая число элементов в соответствующей области (в пересечении, без пересечения).

Читайте также: