Алгоритм шифрования rsa уязвимость при создании цифровой электронной подписи
Обновлено: 06.07.2024
Постановка задачи: во многих публикациях отмечается, что неверный выбор параметров шифра RSA может привести к уменьшению его криптостойкости. В некоторых случаях открытый и закрытый ключи могут полностью совпасть и тогда абонент случайно опубликует секретный ключ . Целью работы является доказательство возможности формирования ключей близнецов, когда открытый и закрытый ключ полностью совпадают. Используемые методы: возможность формирования ключей близнецов теоретически обоснована с помощью восьми лемм . Наличие ключей близнецов подтверждено проведёнными расчётами с помощью математической системы Mathcad. При проведении расчётов были рассмотрены функции Эйлера , кратные десяти, и открытые экспоненты, которые оканчивались цифрами 1 и 9. Новизна: показано, что при значениях функции Эйлера , кратных десяти, существует вероятность открытой публикации секретного ключа , если открытая экспонента оканчивается на цифры 1 или 9. Функция Эйлера формируется кратная десяти, если хотя бы одно простое число оканчивается единицей. Результат: расчётным путём подтверждена возможность формирования ключей близнецов. Практическая значимость: полученные результаты позволяют повысить криптостойкость шифра RSA путём проверки на совпадение сформированных открытых и закрытых ключей и тем самым предотвратить атаку на ключи близнецы.
Похожие темы научных работ по математике , автор научной работы — Алексеев Александр Петрович
Анализ быстродействия алгоритмов вычисления секретного ключа в асимметричной криптосистеме RSA Новая семантически стойкая система шифрования с открытым ключом на базе RSA Генерирование ключа дешифрования для криптосистемы RSA с применением минимально избыточной модулярной системы счисления Примитивы криптосистем с открытым ключом: конечные некоммутативные группы четырехмерных векторов i Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.Vulnerabilities Algorithm for Computing the Secret Key in the RSA Cryptosystem
Текст научной работы на тему «Уязвимости алгоритма вычисления секретного ключа в криптосистеме RSA»
Системы управления,связи и безопасности №3. 2015
Уязвимости алгоритма вычисления секретного ключа в криптосистеме RSA
Постановка задачи: во многих публикациях отмечается, что неверный выбор параметров шифра RSA может привести к уменьшению его криптостойкости. В некоторых случаях открытый и закрытый ключи могут полностью совпасть и тогда абонент случайно опубликует секретный ключ. Целью работы является доказательство возможности формирования ключей близнецов, когда открытый и закрытый ключ полностью совпадают. Используемые методы: возможность формирования ключей близнецов теоретически обоснована с помощью восьми лемм. Наличие ключей близнецов подтверждено проведёнными расчётами с помощью математической системы Mathcad. При проведении расчётов были рассмотрены функции Эйлера, кратные десяти, и открытые экспоненты, которые оканчивались цифрами 1 и 9. Новизна: показано, что при значениях функции Эйлера, кратных десяти, существует вероятность открытой публикации секретного ключа, если открытая экспонента оканчивается на цифры 1 или 9. Функция Эйлера формируется кратная десяти, если хотя бы одно простое число оканчивается единицей. Результат: расчётным путём подтверждена возможность формирования ключей близнецов. Практическая значимость: полученные результаты позволяют повысить криптостойкость шифра RSA путём проверки на совпадение сформированных открытых и закрытых ключей и тем самым предотвратить атаку на ключи близнецы.
Ключевые слова: асимметричная криптосистема RSA, уязвимость, секретный ключ, открытый ключ, функция Эйлера, лемма, простое число, чётное число, нечётное число, числа Ферма.
Криптосистему RSA разработали R. Rivest, A. Shamir, L. Adleman [1], а саму концепцию шифрования с помощью открытого ключа предложили W. Diffie и M. Hellman [2].
Асимметричная криптосистема RSA широко используется в современных инфокоммуникационных системах благодаря своим несомненным достоинствам. Положительными свойствами этой криптосистемы являются возможность передачи приватной информации по незащищённым каналам связи без предварительной передачи секретных ключей с помощью курьеров [3] и обеспечение цифровой подписи финансовых документов [4]. На базе RSA реализована известная почтовая программа PGP [5]. Многие фирмы выпускают микросхемы, которые аппаратно реализуют криптосистему RSA [7].
В работах [9, 10] отмечается, что для формирования ключей необходимо использовать простые числа, длины которых должны быть примерно одинаковые. Для предотвращения факторизации модуля разрядность простых чисел в настоящее время должна быть не менее 1024.. .4096 бит [8, 10].
В ряде публикаций отмечается, что недопустимо использовать открытую экспоненту малой разрядности [10, 14]. При формировании открытой
экспоненты из множества допустимых значений рекомендуют формировать её по случайному закону [7, 11, 13]. В некоторых источниках предлагают
Системы управления,связи и безопасности №3. 2015
использовать открытые экспоненты, которые содержат малое число единиц при их представлении в двоичной системе счисления [7], например, 3, 17, 65537. Это позволяет повысить скорость шифрования, так как уменьшается число операций возведения в степень. В других источниках рекомендуют использовать числа Мерсенна, Ферма [6] и малые нечётные числа [10, 12].
Использование некоторых из перечисленных рекомендаций может привести к появлению уязвимостей в криптосистеме RSA. Взлом криптосистемы возможен путём проведения атаки на наличие ключей близнецов.
Известно, что расчёт секретной экспоненты t в криптосистеме RSA осуществляется с помощью сравнения [1]:
s • t = 1(mod (p(r)), (1)
здесь s - число взаимно простое с p(r), так называемая открытая экспонента; r -произведение двух простых чисел p и q (модуль); p(r) - функция Эйлера, которая вычисляется по формуле:
Из соотношения (1) по вычисленному значению функции Эйлера p(r) и выбранному значению s требуется найти такое значение t, при котором целочисленное деление величины s • на p(r) даст остаток 1.
Для проведения анализа уязвимостей криптосистемы RSA рассмотрим несколько лемм.
Функция Эйлера p(r) является чётным числом.
Функция Эйлера вычисляется по формуле (2). Все простые числа, используемые в криптографии, нечётные, поэтому функция Эйлера, равная произведению двух чётных чисел, является чётным числом.
Множество чисел открытой экспоненты s состоит из множества нечётных чисел.
В соответствии с алгоритмом формирования ключей для асимметричной криптосистемы RSA числа s должны быть взаимно простыми с чётными числами p(r) [1], поэтому числа s будут обязательно нечётными.
Секретная экспонента t является нечётным числом.
В соответствии с выражением (1) целочисленное деление произведения s-t на чётное число p(r) должно дать остаток, равный единице. Это возможно только при нечётных значениях произведения s-t. В соответствии с леммой 2 число s является нечётным. Произведение s-t будет нечётным только при нечётных значениях t.
Системы управления,связи и безопасности №3. 2015
Функция Эйлера кратна 10, если хотя бы одно простое число модуля (p или q) оканчивается на 1.
Используемые в практической криптографии простые числа могут оканчиваться только цифрами 1, 3, 7 и 9. Единственное простое число, которое оканчивается на 5 - это само число 5. Однако оно слишком мало для формирования реальных криптографических ключей. В соответствии с формулой для вычисления функции Эйлера (2) произведение указанных сомножителей будет кратно 10, если хотя бы одно простое число оканчивается на 1.
Считая, что формирование простых чисел происходит по случайному закону, можно ожидать, что 40% ключей создаётся при значениях функции Эйлера, кратной 10.
Если (p(r) кратно 10, а число s оканчивается цифрой 7, то число t оканчивается цифрой 3.
Так как произведение указанных чисел s и t будет оканчиваться единицей, то в результате вычитания единицы из произведения s-t будет получено число, кратное 10.
Таким образом, величину t нужно искать среди чисел, у которых последняя цифра 3, например, 3, 13, 23 и т.д.
Пусть (p(r) = 440, s = 27. Расчёт секретного ключа с помощью обобщённого алгоритма Евклида [12] дал t = 163.
Если (p(r) кратно 10, а число s оканчивается цифрой 3, то число t оканчиваться цифрой 7.
Доказательство аналогично доказательству леммы 5.
Итак, величину t нужно искать среди чисел, оканчивающихся на цифру 7, например, 7, 17, 27 и т.д.
Пусть (p(r) = 440, s = 23, тогда t = 287.
Если cp(r) кратно 10, а s оканчивается цифрой 9, то последняя цифра числа t должна быть 9.
Только произведение двух чисел, оканчивающихся цифрами 9 (при s, оканчивающимся на 9), даёт число, у которого последняя цифра 1. В этих случаях число s t-1 будет кратно 10.
Пусть <p(r) = 120, s = 19. Расчёт дал t = 19.
Системы управления,связи и безопасности №3. 2015
Если p(r) кратно 10, а s оканчивается цифрой 1, то последняя цифра числа t должна быть 1.
Только произведение двух чисел, оканчивающихся цифрами 1 (при числе s, оканчивающимся цифрой 1), даёт число, у которого последняя цифра 1. В этих случаях число s-t-1 будет кратно 10.
Пусть (p(r) = 120, s = 31. Расчёт дал t = 31.
Леммы 7 и 8 указывают на снижение криптостойкости в рассмотренных случаях (последние цифры открытого и закрытого ключей обязательно совпадают). Можно предположить, что могут быть сформированы полностью совпадающие числа s и t (ключи близнецы), то есть секретный ключ может быть ошибочно опубликован абонентом. Примеры 3 и 4 подтверждают это утверждение.
Другими словами, при p(r) кратном десяти и открытых экспонентах, оканчивающихся цифрами 1 и 9 есть вероятность открытой публикации секретного ключа. Если величина s выбирается по случайному закону, то для p(r), кратных 10, вероятность формирования экспонент, оканчивающихся цифрами 1 или 9, составляет 0,2 (половина всех ключей, у которых функция Эйлера кратна десяти). При этом небольшая часть секретных ключей полностью совпадёт с открытыми ключами.
Рассмотренная гипотеза о возможности совпадения открытых и закрытых ключей была проверена расчётным путём с помощью математической системы Mathcad 15. Программа для расчёта ключей приведена в Приложении 1. Для p(r)=440 выявлено 15 уязвимостей (открытый и закрытый ключи полностью совпали, например, 241, 351, 309, 419). Для p(r)=18240 выявлено также 15 ключей близнецов (например, 14401, 14591, 15391). В последнем случае анализировались только ключи, оканчивающиеся на единицу.
Расчёты проводились следующим образом. Выбирались простые числа, которые оканчивались цифрой 1 (в этом случае функция Эйлера будет кратна 10). Для выбранного значения функции Эйлера определялись все допустимые значения открытой экспоненты s. Для значений s, которые оканчивались цифрами 1 или 9, вычислялись секретные экспоненты t. Отмечались совпадающие значения s и t.
Фрагмент протокола выполненных вычислений приведён в таблице 1.
Системы управления,связи и безопасности №3. 2015
Таблица 1. Фрагмент протокола вычислений
(dr) s t (dr) s t (dr) s t
440 21 21 18240 191 191 120 11 11
440 111 111 18240 2431 2431 120 31 31
440 131 131 18240 3041 3041 120 61 61
440 221 221 18240 5281 5281 120 71 71
440 241 241 18240 5471 5471 120 91 91
440 331 331 18240 6271 6271 120 101 101
440 351 351 18240 8321 8321
440 89 89 18240 9121 9121
440 109 109 18240 9311 9311
440 199 199 18240 11551 11551
440 219 219 18240 12161 12161
i Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.440 309 309 18240 14401 14401
440 329 329 18240 14591 14591
440 419 419 18240 15391 15391
440 439 439 18240 17441 17441
При практическом формировании ключей в криптосистеме RSA в случаях, когда функция Эйлера кратна 10, а открытая экспонента оканчивается цифрами 1 или 9, следует произвести проверку на полное совпадение сформированных открытого и зарытого ключей. Очевидно, что совпадающие ключи не должны быть использованы.
Для исключения возникновения ключей близнецов при формировании открытой экспоненты нужно использовать числа, которые оканчиваются на 3 или 7, например, простые числа Ферма 17, 257, 65537.
Определить теоретически число ключей близнецов не представляется возможным. Выполненный объём вычислений в настоящее время мал, поэтому пока невозможно точно определить вероятность возникновения ключей близнецов. Их число нетривиально зависит от значения функции Эйлера. В настоящее время известна только верхняя граница вероятности появления одинаковых ключей (не более 0,2). Отсутствие оценки вероятности возникновения ключей близнецов объясняется необходимостью разработки соответствующего программного обеспечения и большим временем счёта. Если используются 1024-х битные простые числа, то число возможных функций Эйлера оценивается величиной 3,2 10616. Для получения статистически устойчивого результата нужна репрезентативная выборка. Понятно, что время счёта будет внушительным. Однако предотвратить формирование ключей близнецов легко. Для этого достаточно произвести сравнение открытой и закрытой экспонент. Основная цель данной работы показать наличие ключей близнецов. В дальнейшем предстоит получить количественную оценку вероятности их формирования и оценить, насколько имеющееся ограничение уменьшит пространство допустимых ключей.
Системы управления,связи и безопасности №3. 2015
Программа на языке Mathcad 15 для формирования открытой и закрытой
Mathcad 15 Выбор простых чисел pi := 91 ql := Ш1
Общая схема
Схема электронной подписи обычно включает в себя:
- алгоритм генерации ключевых пар пользователя;
- функцию вычисления подписи;
- функцию проверки подписи.
Функция вычисления подписи на основе документа и секретного ключа пользователя вычисляет собственно подпись. В зависимости от алгоритма функция вычисления подписи может быть детерминированной или вероятностной. Детерминированные функции всегда вычисляют одинаковую подпись по одинаковым входным данным. Вероятностные функции вносят в подпись элемент случайности, что усиливает криптостойкость алгоритмов ЭЦП. Однако, для вероятностных схем необходим надёжный источник случайности (либо аппаратный генератор шума, либо криптографически надёжный генератор псевдослучайных бит), что усложняет реализацию.
В настоящее время детерминированые схемы практически не используются.
Функция проверки подписи проверяет, соответствует ли данная подпись данному документу и открытому ключу пользователя. Открытый ключ пользователя доступен всем, так что любой может проверить подпись под данным документом.
Защищённость
Цифровая подпись обеспечивает:
Возможны следующие угрозы цифровой подписи:
- Злоумышленник может попытаться подделать подпись для выбранного им документа.
- Злоумышленник может попытаться подобрать документ к данной подписи, чтобы подпись к нему подходила.
- Злоумышленник может попытаться подделать подпись для какого-нибудь документа.
При использовании надёжной хэш-функции, вычислительно сложно создать поддельный документ с таким же хэшем, как у подлинного. Однако, эти угрозы могут реализоваться из-за слабостей конкретных алгоритмов хэширования, подписи, или ошибок в их реализациях.
Тем не менее, возможны ещё такие угрозы системам цифровой подписи:
- Злоумышленник, укравший закрытый ключ, может подписать любой документ от имени владельца ключа.
- Злоумышленник может обманом заставить владельца подписать какой-либо документ, например используя протокол слепой подписи.
- Злоумышленник может подменить открытый ключ владельца (см. управление ключами) на свой собственный, выдавая себя за него.
Алгоритмы ЭЦП
Управление ключами
Важной проблемой всей криптографии с открытым ключом, в том числе и систем ЭЦП, является управление открытыми ключами. Необходимо обеспечить доступ любого пользователя к подлинному открытому ключу любого другого пользователя, защитить эти ключи от подмены злоумышленником, а также организовать отзыв ключа в случае его компрометации.
Задача защиты ключей от подмены решается с помощью сертификатов. Сертификат позволяет удостоверить заключённые в нём данные о владельце и его открытый ключ подписью какого-либо доверенного лица. В централизованных системах сертификатов (например PKI) используются центры сертификации, поддерживаемые доверенными организациями. В децентрализованных системах (например PGP) путём перекрёстного подписывания сертификатов знакомых и доверенных людей каждым пользователем строится сеть доверия.
Управлением ключами занимаются центры распространения сертификатов. Обратившись к такому центру пользователь может получить сертификат какого-либо пользователя, а также проверить, не отозван ли ещё тот или иной открытый ключ.
Описание алгоритма RSA
Описание RSA было опубликовано в 1977 году Рональдом Ривестом (Ronald Linn Rivest), Ади Шамиром (Adi Shamir) и Леонардом Адлеманом (Leonard Adleman) из Массачусетского Технологического Института (MIT).
Британский математик Клиффорд Кокс (Clifford Cocks), работавший в центре правительственной связи (GCHQ) Великобритании, описал аналогичную систему в 1973 году во внутренних документах центра, но эта работа не была раскрыта до 1977 года и Райвест, Шамир и Адлеман разработали RSA независимо от работы Кокса.
В 1983 году MIT был выдан патент 4405829 США, срок действия которого истёк 21 сентября 2000 года.
Описание алгоритма
Генерация ключей
Для того, чтобы сгенерировать пару ключей выполняются следующие действия:
1. Выбираются два больших простых числа и
2. Вычисляется их произведение
3. Вычисляется Функция Эйлера
4. Выбирается целое такое, что и взаимно простое с
5. С помощью расширенного алгоритма Евклида находится число такое, что
Зашифрование и расшифрование
Число и используется в качестве шифртекста. Для расшифрования нужно вычислить
для некоторого целого , следовательно
Согласно теореме Эйлера:
Некоторые особенности алгоритма
Генерация простых чисел
Для нахождения двух больших простых чисел и , при генерации ключа, обычно используются вероятностные тесты чисел на простоту, которые позволяют быстро выявить и отбросить составные числа.
Для генерации и необходимо использовать криптографически надёжный генератор истинно случайных чисел. У нарушителя не должно быть возможности получить какую-либо информацию о значениях этих чисел.
Выбор значения открытого показателя
RSA работает значительно медленнее симметричных алгоритмов. Для повышения скорости шифрования открытый показатель выбирается небольшим, обычно 3, 17 или 65537. Эти числа в двоичном виде содержат только по две единицы, что уменьшает число необходимых операций умножения при возведении в степень. Например, для возведения числа в степень 17 нужно выполнить только 5 операций умножения:
Выбор значения секретного показателя
Значение секретного показателя должно быть достаточно большим. В 1990 году Михаэль Винер (Michael J. Wiener) показал, что если и , то имеется эффективный способ вычислить по и . Однако, если значение выбирается небольшим, то оказывается достаточно большим и проблемы не возникает.
Длина ключа
Число n должно иметь размер не меньше 512 бит. В настоящий момент система шифрования на основе RSA считается надёжной, начиная с размера N в 1024 бита.
Применение RSA
Система RSA используется для защиты программного обеспечения и в схемах цифровой подписи. Также она используется в открытой системе шифрования PGP.
II. Реализация
Для примера была реализована программа для цифрового подписания файлов и проверки подписей. Использовался алгоритм RSA и сертификаты X.509. Сертификат пользователя выбирается из хранилища сертификатов windows.
Выясняем, как и откуда можно получить электронную подпись на примере криптосистемы RSA.

Содержание
Определения и обозначения
Описание криптосистемы RSA
Асимметричные криптографические системы
Шифрование и дешифрование
Электронная подпись документов
Введение
Наверняка вы сталкивались с таким понятием, как "электронная подпись". Если обратиться к федеральному закону, то можно найти следующее её определение:
«Электронная подпись - информация в электронной форме, которая присоединена к другой информации в электронной форме (подписываемой информации) или иным образом связана с такой информацией и которая используется для определения лица, подписывающего информацию»
Задача ЭП ясна, теперь хотелось бы увидеть и прочувствовать, что именно скрывается за этими двумя словами. Копаясь дальше в гугле, можно найти довольно много различных алгоритмов создания цифровой подписи (DSA, ГОСТ Р 34.10-2012, RSA-PSS и т.д.), разбираться в которых неподготовленному пользователю сложно.
Спасти эту ситуацию и помочь разобраться в том, что есть ЭП, может криптосистема RSA, разработанная Ривестом, Шамиром и Адлеманом в 1978 году. Она не загромождена безумным количеством алгоритмов и основывается на относительно простой математике. В связи с этим можно шаг за шагом прийти от модульной арифметики к алгоритму создания электронной подписи, чему я и хочу посвятить данную статью.
Теорминимум

Сформируем небольшой словарик терминов, которые нам пригодятся далее:
Открытый текст – данные, подлежащие шифрованию или полученные в результате расшифрования
Шифртекст – данные, полученные в результате применения шифра к открытому тексту
Шифр – совокупность обратимых преобразований, зависящая от некоторого параметра (ключа)
Ключ – параметр шифра, определяющий выбор одного преобразования из совокупности.
Факторизация – процесс разложения числа на простые множители.
НОД – наибольший общий делитель.
Числа a и b называются взаимно простыми, если НОД этих чисел равен 1.
Функция Эйлера φ(n) – функция, равная количеству натуральных чисел, меньших n и взаимно простых с ним.
Хочу отметить, что на данном этапе подразумевается, что вы знакомы с арифметическими операциями по модулю. Если нет, то здесь можно о них почитать.
Как оно устроено
Прежде, чем окунуться в необъятный мир математики рассмотреть, как именно устроена RSA, обратимся к тому, как работают
Асимметричные криптосистемы
Рассмотрим задачу сохранности содержимого посылки при передаче от отправителя к адресату. Вот картинка с многим полюбившимся Алисой и Бобом:
Теперь к математике
Асимметричные криптографические системы основаны на так называемых односторонних функциях с секретом. Под односторонней понимается такая функция я y=f(x), которая легко вычисляется при имеющемся x, но аргумент x при заданном значении функции вычислить сложно. Аналогично, односторонней функцией с секретом называется функция y=f(x, k), которая легко вычисляется при заданном x, причём при заданном секрете k аргумент x по заданному y восстановить просто, а при неизвестном k – сложно.
Подобным свойством обладает операция возведения числа в степень по модулю:
Что есть что разобрались, теперь перейдём к конкретике, а именно – генерации ключей Боба. Давайте выберем число n такое, что:
где p и q – некоторые разные простые числа. Для такого n функция Эйлера имеет вид:
Такой выбор n обусловлен следующим. Как вы могли заметить ранее, закрытый ключ d можно получить, зная открытый e. Зная числа p и q, вычислить функцию Эйлера не является вычислительно сложной задачей, ровно как и нахождение обратного элемента по модулю. Однако в открытом ключе указано именно число n. Таким образом, чтобы вычислить значение функции Эйлера от n (а затем получить закрытый ключ), необходимо решить задачу факторизации, которая является вычислительно сложной задачей для больших n (в современных системах, основанных на RSA, n имеет длину 2048 бит).
Возвращаемся к генерации ключей. Выберем целое число e:
Для него вычислим число d:
Для отыскания числа, обратного по модулю, можно воспользоваться алгоритмом Евклида.
Мы завершили с этапом генерации ключей. Теперь Боб публикует свой открытый ключ (e, n), прячет закрытый d, а мы переходим к Алисе.
Шифруем, дешифруем.
Здесь за с обозначен шифртекст, который Алиса будет должна передать Бобу. Отметим также, что c ∈ [1, n − 1], как и m. Расшифруем шифртекст, возведя его в степень закрытого ключа Боба d:
А теперь ответим на вопрос, почему m ≡ m′ . Ниже я приведу доказательство данного утверждения, но если оно (доказательство) вам не сильно интересно, то можете его пропустить и просто поверить, что это так.
Здесь нам понадобится теорема Эйлера:
Также полезной будет китайская теорема об остатках:

Ещё раз напишем две ключевые формулы шифрования и расшифрования соответственно:
Если Алиса получила, что m ≡ m′, то подпись считается правильной.
Дочитавших до этого места хочу поздравить с получением первой цифровой подписи "на бумаге"!

Подпись документов
Рассмотренный алгоритм получения подписи изящен и прост в осознании, однако операция возведения в степень несколько "мешается". Наша текущая задача – подписать объёмный документ. Чтобы сэкономить время, мы не будем подписывать содержимое документа, а прибегнем к помощи хэш-функций (если вы не знаете, что такое хэш-функция, рекомендую почитать википедию). Скажу лишь то, что выходная последовательность хэш-функции имеет небольшую (по сравнению с размером ключей) длину, а также по имеющемуся хэшу нельзя однозначно восстановить исходные данные.
На картинках наглядно показано, в какой момент мы используем хэширование. Создание подписи:
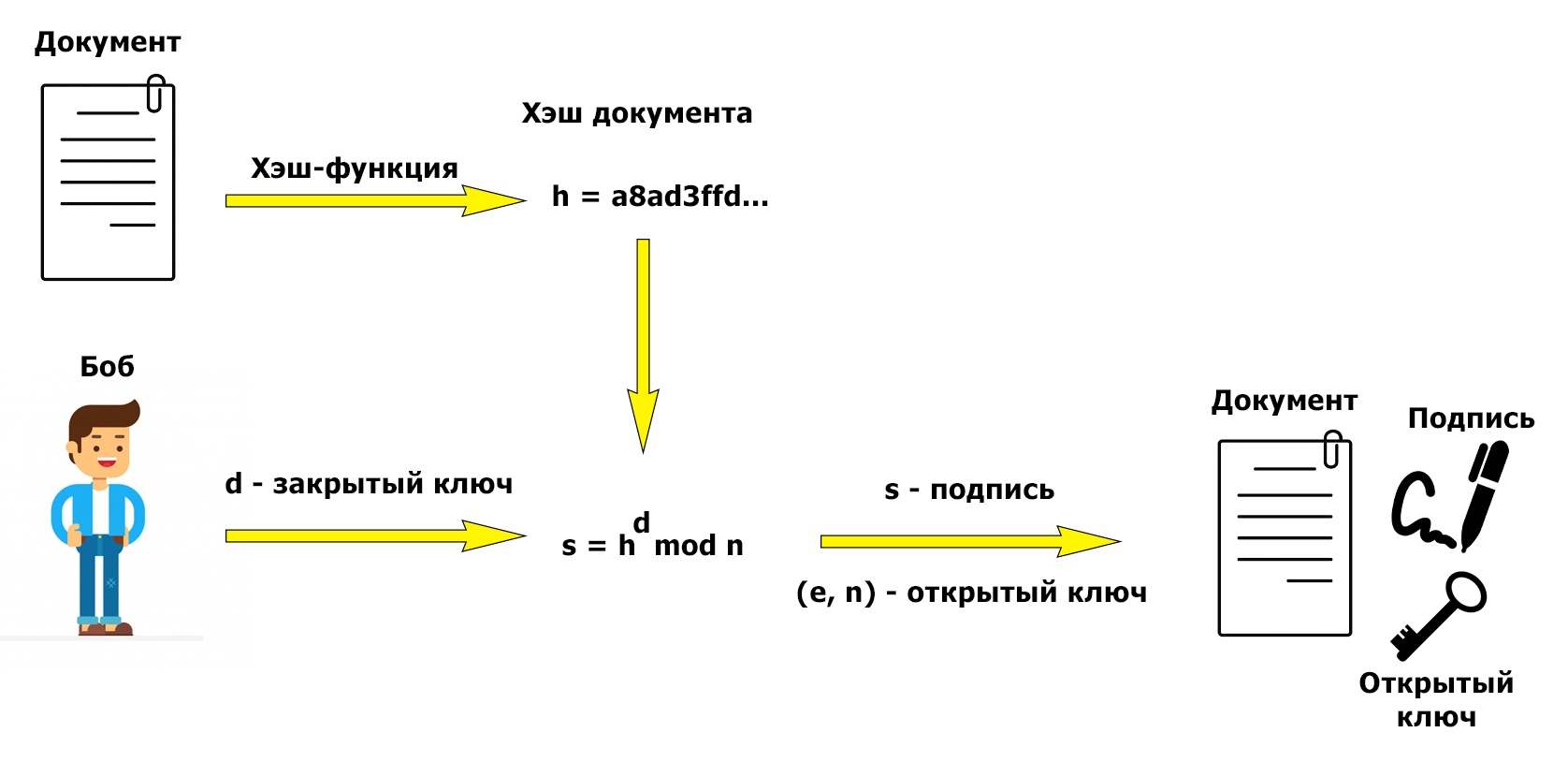

В качестве хэш-функции можно использовать SHA-256, как это сделано, например, в PGP. По теме практического создания электронной подписи с использованием PGP на хабре уже написана статья, поэтому на этом месте имеет смысл поставить точку и перейти к заключению.
Заключение
Вот мы и прошли все стадии создания электронной подписи, начиная с простой модульной арифметики и заканчивая, собственно, получением подписи. Обладая этими знаниями, вы можете попробовать перевести их на ваш любимый язык программирования и написать свою защищенную аську, например. В том, как именно их применить, вас ограничит только ваше воображение.
Отмечу, что другие существующие алгоритмы создания ЭП основаны на схожих принципах, поэтому надеюсь, что после прочтения этой статьи вам будет проще разобраться в них. "Следующей по сложности" я обозначу криптосистему Эль-Гамаля, но о ней уже не в этом посте.
Спасибо за внимание!
Источники
Handbook of Applied Cryptography by A. Menezes, P. van Oorschot and S. Vanstone
Криптографические методы защиты информации: учеб. пособие / С. М. Владимиров, Э. М. Габидулин, А. И. Колыбельников, А. С. Кшевецкий; под ред. А. В. Уривского. – М.: МФТИ, 2016
Маховенко Е. Б. Теоретико-числовые методы в криптографии — М.: Гелиос АРВ, 2006.
NIST Special Publication 800-57 Part 3 Revision 1
Молдовян Н.А. Теоретический минимум и алгоритмы цифровой подписи. – СПб.: БХВ-Петербург, 2010. - Учебное пособие
Цель лекции: познакомиться с некоторыми алгоритмами формирования и проверки электронной цифровой подписи ( ЭЦП , ЭП).
Электронная подпись на основе алгоритма RSA
В результате каждый пользователь имеет свои собственные открытый (состоящий из двух частей) и закрытый ключи. Затем пользователи обмениваются открытыми ключами. Это подготовительный этап протокола.
Основная часть протокола состоит из следующих шагов.
Возможность применения алгоритма RSA для получения электронной подписи связана с тем, что секретный и открытый ключи в этой системе равноправны. Каждый из ключей, d или e , могут использоваться как для шифрования, так и для расшифрования. Это свойство выполняется не во всех криптосистемах с открытым ключом.
Алгоритм RSA можно использовать также и для обмена ключами.
Цифровая подпись на основе алгоритма Эль-Гамаля
Принцип создания и проверки подписи

. Таким образом, каждый пользователь получает пару (закрытый ключ; открытый ключ) = (Хi, Yi) . Открытые ключи пользователей могут храниться в общей базе системы распределения ключей и при необходимости предоставляться всем абонентам системы.

- Первый пользователь выбирает случайное секретное число k , взаимно простое с Р-1 , и вычисляет число
- Затем с помощью расширенного алгоритма Евклида необходимо найти значение b в следующем уравнении:
Пример вычисления и проверки цифровой подписи
Затем пользователь выбирает случайное секретное число k , взаимно простое с Р-1 . Пусть k=9 ( 9 не имеет общих делителей с 10 ). Далее необходимо вычислить число

После этого с помощью расширенного алгоритма Евклида находится значение b в уравнении:

Решением последнего уравнения будет значение b=9 .


Это пятый урок из цикла «Погружение в крипту». Все уроки цикла в хронологическом порядке:
-
Основы и исторические шифраторы. Как работают (и анализируются) шифры сдвига, замены, Рихарда Зорге, шифр Вернама и шифровальные машины Что это такое, как выполняется распределение ключей и как выбрать криптостойкий ключ Что такое сеть Фейстеля и какими бывают отечественные блочные шифры, используемые в современных протоколах, — ГОСТ 28147—89, «Кузнечик» В чем разница между 3DES, AES, Blowfish, IDEA, Threefish от Брюса Шнайера и как они работают
- Урок 5. Электронная подпись. Виды электронных подписей, как они работают и как их использовать (ты здесь)
- Урок 6. Квантовая криптография. Что это такое, где используется и как помогает в распределении секретных ключей, генерации случайных чисел и электронной подписи
Как работает цифровая подпись
Если ты читал вторую часть нашего цикла, то помнишь, что существуют симметричный и асимметричный подходы к шифрованию. С электронной подписью дела обстоят очень похоже — есть подписи с симметричным механизмом, а есть с асимметричным.
Симметричный механизм подписи малоприменим на практике — никому не хочется генерировать ключи для каждой подписи заново. А как ты помнишь, именно в одинаковых ключах кроется фишка симметричной криптографии.
Схемы электронной подписи так же многообразны, как и способы шифрования. Чтобы схема подписи была стойкой, нужно, чтобы она основывалась на трудновычислимой математической задаче. Есть два типа таких задач: факторизация больших чисел и дискретное логарифмирование.
Факторизация больших чисел
Рассмотрим на практике электронную подпись на основе знаменитого алгоритма RSA. Шифрование RSA мы рассматривать не стали — это мейнстрим, и в той же «Википедии» есть его подробное описание.
1. Генерация ключей
Причина стойкости RSA кроется в сложности факторизации больших чисел. Другими словами, перебором очень трудно подобрать такие простые числа, которые в произведении дают модуль n. Ключи генерируются одинаково для подписи и для шифрования.

Когда ключи сгенерированы, можно приступить к вычислению электронной подписи.
2. Вычисление электронной подписи

3. Проверка электронной подписи

RSA, как известно, собирается уходить на пенсию, потому что вычислительные мощности растут не по дням, а по часам. Недалек тот день, когда 1024-битный ключ RSA можно будет подобрать за считаные минуты. Впрочем, о квантовых компьютерах мы поговорим в следующий раз.
В общем, не стоит полагаться на стойкость этой схемы подписи RSA, особенно с такими «криптостойкими» ключами, как в нашем примере.
Дискретное логарифмирование
Это вторая сложная проблема, на которой основаны цифровые подписи. Для начала хорошо бы усвоить, что такое дискретный логарифм. Для кого-то такое словосочетание может звучать пугающе, но на самом деле это одна из самых простых для понимания вещей в этой статье.
Предположим, дано уравнение 4x = 13 (mod 15) . Задача нахождения x и есть задача дискретного логарифмирования. Почему же она так сложна для вычисления? Попробуй решить это уравнение перебором! Компьютер, ясное дело, будет более успешен, но и задачи дискретного логарифмирования обычно далеко не так просты. Возьмем для примера схему Эль-Гамаля.
1. Генерация подписи

2. Проверка подписи

Даже если не вникать в схему, понятно, что такой алгоритм сложнее. Кроме того, нигде уже не используется простой модуль, его сменили эллиптические кривые. Эллиптическая кривая — это кривая, которая задана кубическим уравнением и имеет невообразимо сложное представление. Задача решения логарифма в группе точек, которые принадлежат эллиптической кривой, вычислительно сложная, и на данный момент не существует таких мощностей, которые решали бы это уравнение за полиномиальное время, если длина секретного ключа составляет 512 бит. Согласно задаче дискретного логарифмирования, невероятно сложно найти на кривой две такие точки, которые связывает операция возведения в некоторую степень.
ЭЦП на практике
В России, как и во многих развитых странах, электронная подпись имеет официальный юридический статус. У нас этот факт регламентирует закон № 63-ФЗ «Об электронной подписи». Однако он утверждает, что юридической силой обладает далеко не любая электронная подпись, а только соответствующая определенным критериям:
- подпись сгенерирована посредством криптографического преобразования с секретным ключом;
- этот ключ и соответствующий ему открытый ключ выданы квалифицированным удостоверяющим центром;
- по подписи можно достоверно установить ее обладателя.
Подпись также должна быть вычислена средствами, соответствующими требованиям закона. Этим требованиям удовлетворяет отечественный алгоритм шифрования ГОСТ 34.10—2012. Он использует математический аппарат эллиптических кривых, является достаточно стойким и официально используется для разработки криптографических средств, реализующих электронную подпись. Для того чтобы попробовать неквалифицированную подпись — без сертификата удостоверяющего центра, можно воспользоваться известной PGP. Потестировать подпись можно, к примеру, на сайте ReadVerify.
Стоит сказать, что в нашей стране электронная подпись используется чаще, чем можно себе представить. В банках, налоговых, торгово-закупочных операциях, бухгалтерии — во всех этих организациях используется или внедряется ЭЦП. Электронная подпись отважно борется со злом бюрократии, однако до полной победы еще далеко.
За рубежом электронный документооборот процветает еще дольше. Официальный стандарт электронной подписи в США DSS (Digital Signature Standard) также использует эллиптические кривые и основан на описанной выше схеме Эль-Гамаля.
Цифровая подпись в Bitcoin
Помимо прочего, электронная подпись используется в криптовалютах, в частности — в Bitcoin. У каждого пользователя Bitcoin есть пара из секретного и открытого ключа. Хеш-значение открытого ключа служит основным адресом для передачи монет. Это значение не секретно, и сообщать его можно кому угодно. Но по значению хеша вычислить значение открытого ключа невозможно.
Сама пара ключей будет использована лишь однажды — при передаче прав собственности. На этом жизнь пары ключей заканчивается.
- PUB1 — публичный ключ;
- PRIV1 — секретный ключ;
- HASH1 или HASH(PUB1) — хеш-значение открытого ключа (биткойн-адрес);
- HASH2 или HASH(PUB2) — хеш открытого ключа следующего владельца.
Вот как устроен сам процесс передачи прав собственности на биткойны.
- Владелец монеты открыто сообщает хеш своего публичного ключа HASH(PUB1), это и будет идентифицировать биткойн.
- До момента продажи оба ключа PUB1, PRIV1 продавца остаются в секрете. Известен только HASH(PUB1) и соответствующий ему биткойн.
- Как только появляется покупатель, владелец формирует открытое письмо, в котором указывает адрес биткойна HASH(PUB1) и хеш-значение публичного ключа нового владельца HASH(PUB2). И конечно же, подписывает письмо своим секретным ключом PRIV1, прилагая публичный ключ PUB1.
- После этого пара ключей владельца PUB1 и PRIV1 теряют свою актуальность. Публичным ключом можно проверить само письмо, узнать новый адрес монеты.
О втором собственнике ничего не известно, кроме HASH(PUB2), до тех пор пока он не передаст права третьему владельцу. И эта цепочка может быть бесконечной.
Подписывая передачу прав с использованием ЭЦП, собственник подтверждает не только свою личность, но и свое согласие на проведение сделки. То есть вернуть монетку он уже не может и с этим согласился, подписавшись электронной подписью.
Благодаря HASH(PUB) получается двойная защита. Первая загадка — узнать публичный ключ по его хешу. Вторая загадка — подписаться чужим секретным ключом.
Такая технология построения цепи передачи прав и называется блокчейном. Благодаря этой технологии можно отследить историю владения до самых истоков, но изменить эту историю никак нельзя.
Выводы
Будущее неразрывно связано с криптографией. В один прекрасный момент при получении паспорта наши дети будут генерировать электронную подпись и покупать чипсы в ларьке за криптовалюту. Что готовит нам будущее с точки зрения развития криптографии, посмотрим в следующей статье на примере квантовых компьютеров.
Читайте также:

