Что такое сплайн в компьютерной графике

Обновлено: 07.07.2024

Вообще сплайн - это линия (кривая, ломанная) какая угодно. Сами по себе сплайны не отображаются при рендере, а служат вспомогательными средствами. Создать сплайн вы можете перейдя во вкладку Create - Shapes - Splines.

Вот основные формы сплайнов, которыми я обычно пользуюсь:

Когда вы создаете любой тип сплайнов, то после изменения параметров, для дальнейшего редактирования, вам необходимо нажать на него правой кнопкой и выбрать Convert To - Convert To Editiable Spline, или применить модификатор Edit Spline из списка модификаторов.

Все сплайны состоят из точек (vertex) и сегментов (segment):

Точки бывают четырех типов:

1. Corner - точка образует ломаную.
2. Smooth - автоматически сглаживает линию, образуя кривую.
3. Bezier - так же образует сглаженую линию, но формой изгиба можно манипулировать с помощью специальных маркеров.
4. Bezier corner - в отличии от bezier маркеры несимметричны.

Чтобы изменить тип точки нужно выделить одну или несколько точек и нажать правую кнопку мыши. В контекстном меню выбрать нужный тип.
В разеделе Modify сплайны имеют несколько вкладок: Rendering, Interpolation, Selection, Soft Selection и Geometry.

Вкладка Rendering:

Enable in rendering - включает отображение сплайна при рендере.

Enable in Viewport - включает отображение сплайна в окнах вьюпорта.

Radial - сплайн будет иметь форму веревки (то есть круг в сечении).

Thickness - толщина или диаметр круга в сечении.

Sides - количество сторон круга (если выбрать 3, то в сечении будет треугольник).

Angle - Угол поворота сечения.

Rectangular - сплайн будет иметь форму доски (то есть прямоугольник в сечении).

Length - длинна прямоугольника в сечении.

Width - ширина прямоугольника в сечении.

Aspect - соотношение длинны и ширины друг к другу.

Auto Smooth - включает автоматическое сглаживание.

Вкладка Interpolation:

Steps - количество сегментов между каждыми двумя точками сплайна (для сглаженных форм требуется большее количество, для ломаной линии достаточно нуля ).

Optimize - автоматически убирает сегменты, которые не влияют на форму сплайна.

Adaptive - автоматически подбирает количества сегментов, для получения идеально гладкой формы.

Вкладка Geometry:

New vertex type - Выбор тип вновь созданных точек.

Create line - Создать дополнительную линию с сплайне.

Attach - Присоеденить линию к сплайну.

Refine - Вставить точку в любое место сплайна.

Weld - Слить соседние точки в одну (справа указано минимальное расстояние между точками, при котором они будут слиты)

Connect - Соеденить две точки линией.

Insert - Продолжить линию (нажимаете Insert затем на крайнюю точку и продолжаете создание сплайна)

Fillet - Скругление углов (выделяете точку и задаете радиус скругления)

Chamfer - Создание фаски (выделяете точку и задаете размер фаски)

Divide - Разделяет выбранный сегмент на указанное количество точек.

Использование модификатора Shell, на примере создания объемного текста.

Создаем сплайн Text:

В поле Text меняем текст на нужный, изменяем размер (Size). Выбираем и стека модификаторов Shell. Затем задаем нужную степень выдавливания (Inner Amount или Outer Amount)

Модификатор Shell можно применять только к закрытым сплайнам (не имеющим разрывов). Вот пример использование модификатора Shell на сплайны Text, Line, NGon и Star:

Модификатор Sweep.

Сперва создаим любую линию. Я создал Line с прямыми углами (создается с нажатой клавишей Shift)

Далее из списка модификаторов выбираем Sweep и получаем следующий результат:

Я думаю Вам не составит труда разобраться в настройках модификатора. Самое основное - это выбор формы сечения и параметров этой формы (радиуса или длинны, ширины, толщины)

Модификатор Lathe.

Поздравляю! Вы дошли до самой интересной части урока.
Модификатор Lathe используется для создания объектов имеющих симметрию вращения (это могуть быть кувшины, бокалы, бутылки, колонны, стаканы и много другое).
Все что вам потребуется это нарисовать вертикальную линию в проекции Font и выбирать из списка модификаторов Lathe:

Нам сразу же нужно переместить ось симметрии, для этого нажимаем на плюсик справа от названия модификатора и выбираем Axis. Перемещаем Axis по оси Х :

Далее возможны два случая:
1. Поверхность отображается нормально (в том цвете, который у вас выбран) - тогда все хорошо.
2. Поверхность черная - значит нужно вывернуть её наизнанку поставив галочку на Flip Normals.

Теперь проверьте включена ли у вас кнопка Show end result on/off toggle, которая находится под списком модификаторов. Включить её нужно для того, что бы видеть эффект всех модификаторов назначенных объекту:

Далее переходим к редактированию вершин (нажимаем на плюс слева от Line и выбираем Vertex), добиваемся желаемого результата. Можете добавлять\удалять точки, менять их тип и т.д.

Модификатор Lathe имеет несколько параметров, вот основные из них:

Degrees - показывает на сколько градусов проворачивается сплайн вокруг оси симметрии (по умолчанию 360 градусов, полный оборот).

Flip Normals - выворачивает поверхность наизнанку.

Segments - количество сегментов ( сглаженность фигуры).

На этом третий урок окончен. В этот раз видеоурок состоит из двух частей:

Определение 5.2.1. Сплайном называется кривая, построенная по совокупности точек которые называются характеристическими или опорными точками сплайна. Требуется, чтобы сплайн r = r(t) проходил через заданные точки при заданных значениях параметра Значения параметра называются узловыми, а точки на оси R - узлами сплайна.

Пример 5.2.1. Ломаная линия с вершинами в точках :

$r(t) = p_i(1-\omega)+p_i+1\omega,$

где -t_i>" />
и ." />
Параметр называется местным параметром на учacткe ." />

Если то параметризация ломаной называется равномерной. В этом случае параметрическая длина ломаной равна т. е. -числу опорных точек минус 1, если все опорные точки различны.

Если т. е. ломаная замкнута, ее параметрическая длина равна числу опорных точек (в предположении, что точки " />
различны):

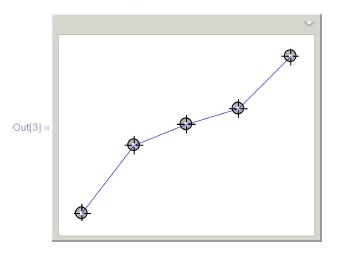
Рассмотрим основные примеры сплайнов.

Сплайн Лагранжа

Пусть дана опорная точка Требуется найти полиномиальную по кривую такую, что при заданных значениях параметра Будем искать решение этой задачи в виде

$r(t)=\sum_<i=0> ^L(t_i)p_i,$

$L_i(t_j)= \delta_<ij> = \begin 1, i=j,\\ 0, i \ne j, \end 0 \le i,j \le n$

Таким свойствами обладают многочлены

$L_i(t)=\frac<(t-t_0) \dots (t-t_<i-1> )(t-t_)\dots (t-t_n)>)(t_i-t_) \dots (t_i-t_n)>=\frac<\Pi_<j=0, i \ne j>^(t-t_j)><\Pi_<j=0, j \ne i>^(t_i-t_j)>$

С их помощью получаем сплайн Лагранжа:

$r(t)=\sum_<i=0> ^\frac<\Pi_<j=0, i \ne j>^(t-t_j)><\Pi_<j=0, j \ne i>^(t_i-t_j)>p_i$

$r(t)=\sum_<i=0> ^\frac(t)>$

$w_<0,n> (t) = (t-t_0) \dots (t-t_n),\\ w_$

Главный недостаток сплайнов Лагранжа состоит в том, что между двумя соседними опорными точками они могут образовывать петли. Такие петли, не обусловленные расположением опорных точек, называются необоснованными петлями и являются существенным недостатком сплайна, не позволяющим применять данный сплайн для большинства приложений компьютерной геометрии.

Еще один существенный недостаток сплайнов Лагранжа состоит в том, что они могут выходить за пределы выпуклой оболочки своих опорных точек, причем довольно значительно.

Эти недостатки - цена за бесконечную гладкость сплайна на всей области определения параметра. Поэтому в компьютерной геометрии чаще всего пользуются не гладкими, а кусочно-гладкими сплайнами, о которых пойдет речь ниже.

Пример 5.2.2. Сплайн Лагранжа с возможностью управления опорными точками:

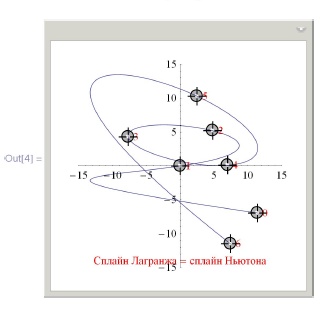
Сплайн Ньютона

Сплайн Ньютона представляет собой тот же самый сплайн Лагранжа, но в другой форме, удобной для перевычисления сплайна в случае добавления новых опорных точек.

А именно, сплайн Ньютона записывается в виде

$r(t) = a_0 + a_1(t - t_0) + a_2(t - t_0)(t - t_1) + \dots + a_n(t - t_0) \dots (t - t_<n_1> ),$

где векторные коэффициенты ищутся из условий прохождения сплайна через точки При этом точки полностью определяют коэффициенты с помощью системы уравнений

$\begin p_0 = a_0,\\ p_1=a_0+a_1(t_1-t_0),\\ p_2 = a_0 + a_1(t_2 - t_0) + a_2(t_2 - t_0)(t_2 - t_1),\\ . \\ p_n = a_0 + a_1(t_n - t-0) + a_2(t_n - t_0)(t_n - t_1) + \dots +a_n(t_n-t_0) \dots (t_n-t_) \end$

Эта система решается за один проход, так как матрица системы является нижнетреугольной. Из первых уравнений определяются первые неизвестные ." />
Поэтому если мы добавим еще одну точку ," />
нам будет нужно лишь определить еще один коэффициент " />
из еще одного, добавленного уравнения. Коэффициенты при этом останутся прежними.

Задача 5.2.1. Написать программу для сплайна Ньютона с возможностью добавлять точку.

Сплайн Эрмита

Сплайны Эрмита предназначены для соединения двух заданных кривых новой кривой, полиномиальной по параметру, так, чтобы получившаяся совокупная кривая имела заданную степень гладкости в точках стыковки. Отсюда следует, что сплайн Эрмита задается двумя своими крайними точками и заданным числом m производных радиус-вектора в каждой из крайних точек. Сплайн Эрмита имеет вид полинома степени по Степень полинома называется порядком сплайна. При этом векторных коэффициентов этого полинома определяются из системы уравнений ( условие для каждой из двух крайних точек).

Сплайн Эрмита может быть определен формулой

$r(t)=\sum_<i=0>^m(g_i(t,m)r_0^i+h_i(t,m)r_1^i),$

( 5.1)

где - заданные значения радиус-вектора кривой и его производных на концах, а даются формулами

$\beging_i(t,m)=\frac\sum_^C_^t^(1-t)^,\\ h_i(t,m)=(-1)^i \frac\sum_^C_^t^(1-t)^ \end$

( 5.2)

Задача 5.2.2. Написать программу для сплайна Эрмита с возможностью добавлять точку. Запрограммировав сплайны Эрмита, проверить на Mathematica, что производные радиус-вектора на концах сплайна равны заданным значениям.

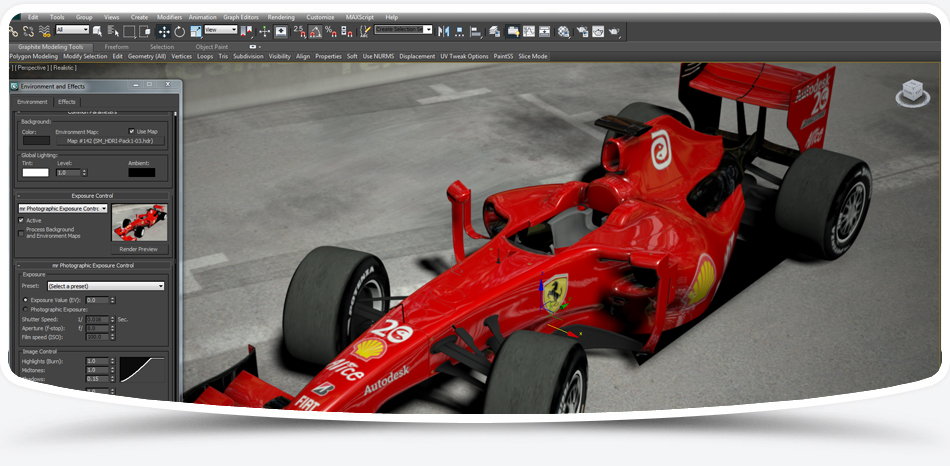
Сплайны (Spline — кусочно-полиномиальная функция) — это двумерные геометрические объекты, которые совершенно самостоятельны и могут служить основой для построения более сложных трехмерных тел. Внешне сплайны представляют собой разнообразные линии, форма линии определяется типом вершин, через которые она проходит. Сплайнами могут быть как простейшие геометрические фигуры: прямоугольники, звезды, эллипсы и пр., так и сложные ломаные или кривые, а также контуры текстовых символов.

Основными элементами сплайнов являются вершины (Vertex) и сегменты (Segment). Вершинами называют точки, расположенные на сплайне, при этом первая вершина, обозначающая начало сплайна, отмечается квадратиком белого цвета. Под сегментом принято понимать участок линии сплайна, ограниченный двумя соседними вершинами, — сегменты могут быть как прямо-, так и криволинейными отрезками. Вершины сплайна различаются по типу, от которого зависит степень кривизны прилегающих к данным вершинам сегментов сплайна. Всего выделяют четыре типы вершин (рис. 1):
Corner (Угловая) — вершина, в которой сплайн имеет излом, а примыкающие к ней сегменты лишены кривизны.
Smooth (Сглаженная) — вершина, через которую кривая сплайна проводится с плавным изгибом, а кривизна прилегающих к вершине сегментов одинакова с обеих сторон.
Bezier (Безье) — вершина, напоминающая сглаженную и отличающаяся от нее возможностью управления степенью кривизны обоих сегментов. Последнее осуществляется благодаря наличию в вершине касательных векторов, ограниченных на концах маркерами в виде квадратиков зеленого цвета и называемых ручками Безье. Перемещая ручки Безье, можно изменять направление, в соответствии с которым сегменты сплайна входят в вершину и выходят из нее, а изменяя расстояние от маркеров до вершины — регулировать степень кривизны сегментов сплайна. У вершин данного типа ручки Безье связаны между собой, и перемещение одной из них автоматически вызывает перемещение второй.
Bezier Corner (Безье угловая) — вершина, имеющая касательные векторы, позволяющие управлять степенью кривизны сегментов, однако, в отличие от вершин Bezier, у вершин Bezier Corner касательные векторы не связаны друг с другом и перемещение одного из маркеров не зависит от перемещения другого.

Сегменты также различаются по типу: Curve (Кривая) или Line (Линия). Выбрав типа Curve, можно получить криволинейные сегменты, если вершины являются гладкими или имеют тип Безье, в случае же угловых вершин даже при установке типа Curve сегмент останется линейным. Выбор типа Line приводит к игнорированию типа вершин, в результате чего сегмент данного типа всегда выглядит линейным.

Сплайны имеют многочисленные применения как в математической теории, так и в разнообразных вычислительных приложениях. В частности, сплайны двух переменных интенсивно используются для задания поверхностей в различных системах компьютерного моделирования.

Содержание

Определение и история

Вторая производная кубического сплайна на рисунке выше.

Рассмотрение сплайнов начнем с определения алгебраического сплайна []: Функция определенная и непрерывная на отрезке , называется полиномиальным сплайном порядка с узлами , если на каждом из отрезков ,x_j)\," width="" height="" />
, является алгебраическим полиномом степени, не превышающей , а в каждой из точек некоторая производная (t)\," width="" height="" />
может иметь разрыв. Если в точке непрерывные функции >(t),>. >)>>(t)\," width="" height="" />
, а производная )>>(t)\," width="" height="" />
в точке терпит разрыв, число называют дефектом сплайна. Множество \," width="" height="" />
называют сеткой узлов сплайна, а точки узлами или точками соприкосновения или склейки сплайна.

Для определения интерполяционного сплайна с непрерывной первой производной, достаточно рассчитать значение первой производной в узлах. Способ определения производных в узлах сплайна определяет широкое разнообразие интерполяционных сплайнов. Часто производные определяются не как константы, а как некоторые зависимости от интерполируемой функции и сетки интерполяции.

Если значение первой производной в узлах рассчитывать исходя из условия непрерывности второй производной (решая систему с n линейных уравнений), то сплайн будет иметь две непрерывные производные. Такой способ построения сплайна, как и сам сплайн называют глобальным, поскольку при определении каждого из его коэффициентов учитывается все множество узлов интерполяции.

В других случаях, для определения отдельного коэффициента учитываются только ближайшие узлы интерполяции и такие способы построения, как и сами сплайны, называют локальными. Параметры фрагмента такого сплайна можно определить независимо от других фрагментов.

Простым условием построения фрагмента локального сплайна является условие равенства полинома на концах отрезков соответствующим значениям интерполируемой функции.

$P_j(t_j) = f(t_j), \qquad P_j(t_ ) = f(t_) \qquad (1)$

Система из 4-х уравнений

$P_j^ () = (), \qquad P_j^(>) = (>)\qquad (4)$

Классификация сплайнов

Как отмечалось выше, существует большое количество конструкций, которые называют сплайнами. Поэтому необходимо внести определенную классификацию в это многообразие, имея целью выделить те признаки, которые позволят выбрать сплайны годные для конкретной прикладной задачи.

Вид фрагментов сплайна. То, что сплайн состоит из фрагментов одинакового вида, является одним из ключевых признаков, что отличает его от других кусковых функций.

Экспоненциальные сплайны. Если гибкую металлическую линейку, зафиксированную в узлах, натянуть, то решением дифференциального уравнения будет не алгебраический полином, а экспонента. Поэтому такие сплайны называют также напряженными. Экспонента описывает многие физические процессы в динамических системах. Недостатком является трудоёмкость расчета.

Также существуют рациональные сплайны и сплайны Паде. Их особенностью является возможность разрыва производных на фрагментах, при непрерывности в узлах. М. Ансерме строит фракциональные сплайны, где фрагменты заданы с помощью гамма-функции.

Ширина фрагментов. Следует выделить сплайны с равной шириной фрагментов. Это позволяет значительно упростить расчетные выражения, ускорить работу алгоритмов и снизить затраты на реализацию. Определенного упрощения можно достичь за счёт применения фрагментов с кратной шириной. Существуют сплайны с нулевой шириной фрагментов (Де Бур). Это приводит к кратности узлов и возможности приближать сплайны с неразрывными фрагментами разрывных функций. Расчетные выражения получают в результате предельных переходов. Сплайны могут иметь также фрагменты с бесконечной шириной. Эти фрагменты должны быть крайними. Иногда это позволяет естественно задать краевые условия.

Условия стыковки фрагментов. Еще один важный признак, что отличает сплайны. Когда идет речь о сплайнах, как правило, считают, что фрагменты стыкуются гладко. То есть обеспечивается непрерывность значений и первой производной. Понятие дефекта сплайна связано с числом непрерывных производных, которые имеет функция-фрагмент определенного вида и числом производных, непрерывность которых гарантирована в узлах. Экспонента, синусоида имеют бесконечное число производных. Для них это понятие не имеет смысла. Поэтому удобнее говорить прямо о числе производных, непрерывность которых гарантирована в узлах сплайна. Практически речь идет о непрерывности значений и первой, максимум второй производной. Разрыв второй и высших производных визуально не заметно, поэтому учитывается редко. Понятно, что первая производная в точках стыка может задаваться по-разному. Наиболее распространены два приёма. Значение первой производной выбирается так, чтобы обеспечить непрерывность второй (глобальные кубические сплайны минимального дефекта). Первая производная равняется первой производной интерполируемой функции (возможно приближенно) в эрмитовых сплайнах.

Дополнительные ограничения. Они чаще всего касаются производных в узлах. Иногда они вытекают из физики процесса. Условия: неотъемлемость значений, равенство моментов, площадей, условия нормирования. Дополнительные условия иногда упрощают анализ свойств сплайнов, но могут серьезно затруднять построение и затраты реализации.

Сетка точек интерполяции. Может существенно влиять на эффективность расчетов. Важны случаи равномерной сетки и равномерной сетки, с расстоянием между точками, кратным расстоянию между узлами сплайна.

Локальные свойства базисных функций. Сплайн можно представить как сумму взвешенных базисных сплайнов. Существенным является ширина этих базисных функций. Так, в глобальных сплайнах базисные сплайны ненулевые на всём отрезке интерполяции. Хотя стоит заметить, что с определенной точностью (достаточной для многих технических расчетов) их можно считать локальными. У локальных сплайнов ширина базисных функций невелика (четыре фрагмента у кубических эрмитовых сплайнов). Это существенно влияет на эффективность расчетов и затраты реализации.

$S(x) = \sum\limits_<j = 1> ^r (x)>$
,

Содержание коэффициентов сплайна. Как отмечалось в предыдущем пункте, содержание параметров сплайна при пофрагментном представлении определяется типом функции. При полиномиальном представлении следует выделить случай, когда коэффициенты имеют тот же физический смысл, что и входные данные. То есть, коэффициенты являются значениями сплайна в узлах. Такую форму называют Лагранжевой, по аналогии с полиномом Лагранжа. Следует заметить, что базисные сплайны этой формы равны единице в центральном узле и нулю во всех остальных.

Особые сплайны. В ряде случаев рассматривают функции, которые находятся близко к границе между сплайнами и обычными функциями, а также сплайнами и кусковыми функциями. К примеру, это сплайны, состоящие из двух фрагментов. Имеют упрощенный вариант построения, но особое внимание следует уделять краевым условиям.

Читайте также: