Фирма выпускает 2 вида мороженого сливочное и шоколадное excel

Обновлено: 01.07.2024

Покажем последовательность решения задачи линейного программирования на примере.

Фирма производит два вида мороженого: сливочное и шоколадное. Для изготовления мороженого используются два исходных продукта: молоко и наполнители, расходы которых на 1 кг готового продукта и их суточные запасы приведены в таблице.

Исходный продукт

Расход исходных продуктов на 1 кг мороженого

Запас, кг

Сливочное

Шоколадное

Суточный спрос на сливочное мороженое превышает спрос на шоколадное не более чем на 100 кг. Кроме того известно, что спрос на шоколадное мороженое не превышает 350 кг в сутки. Отпускная цена 1 кг сливочного мороженого 16 ден. ед., шоколадного – 14 ден. ед.

Требуется определить в каком количестве мороженого каждого вида должна производить фирма, чтобы доход от реализации продукции был максимальным.

Решение.

Шаг 1 – разработка математической модели

Введем обозначения: x₁ – суточный объем производства сливочного мороженого, х₂ - суточный объем производства шоколадного мороженого. Исходя из условия задачи целевая функция будет иметь вид при ограничениях

Шаг 2. Формализация математической модели в электронной таблице

1. На рабочем листе сформируйте табличку, как показано на рис. 33.

2. Полагая, что неизвестные (x₁ и x₂) будут размещаться в ячейках В3 и С3, в ячейку В4 введите формулу целевой функции: = 16*B3+14*C3, а в ячейки В6, В7 и В8 – формулы ограничений (см рис.30).

Рисунок 33

Шаг 3. Настройка инструмента Поиск решения

1. Выполните команду меню Сервис - Поиск решения – откроется диалоговое окно Поиск решения (рис.34).

Рисунок 34

2. Укажите в диалоговом окне ссылки на целевую ячейку, на ячейки, в которых размещены параметры целевой функции, а также введите все ограничения.

3. После щелчка на кнопке ОК в ячейках В3 и С3 будет получено решение - значения x₁ и x₂ , при которых, целевая функция имеет максимальное значение, при заданных ограничениях (рис.35).

Рисунок 35

Таким образом, при выпуске 312,5 кг сливочного и 300 кг шоколадного мороженого максимальный доход от реализации составит 9200 ден.ед.

Рассмотрим нахождение оптимального плана выпуска изделий предприятия на следующем примере.

Пример 1.Фирма выпускает два вида мороженого: сливочное и шоколадное. Для изготовления мороженого используются два исходных продукта: молоко и наполнители, расходы которых на 1 кг мороженого и суточные запасы исходных продуктов даны в таблице.

Исходный продукт	Расход исходных на 1 кг мороженого	продуктов	Запас, кг.
Сливочное	Шоколадное
Молоко	0,8	0,5
Наполнители	0,4	0,8

Изучение рынка сбыта показало, что суточный спрос на сливочное мороженое превышает спрос на шоколадное не более чем на 100 кг.

Кроме того, установлено, что спрос на шоколадное мороженое не превышает 350 кг в сутки. Отпускная цена 1 кг сливочного мороженого 16 руб. ед., шоколадного – 14 руб.

Требуется определить, какое количество мороженого каждого вида должна производить фирма, чтобы доход от реализации продукции был максимальным?

Решение. Обозначим: x₁ – суточный объем выпуска сливочного мороженого, кг; x₂ – суточный объем выпуска шоколадного мороженого, кг.

Составим математическую модель задачи.

Целевая функция будет иметь вид:

Модель (2.1), представленная такой записью ограничений, граничных условий и целевой функции, относится к типу задач линейного программирования. Термин «линейное программирование» объясняется тем, что при подсчете расходов ресурсов на программу выпуска и расчете ожидаемой выручки после реализации всей выпущенной по этой программе продукции используются только линейные функции.

Этап 1.Под допустимым решением задачи ЛП понимается такой числовой набор значений искомых переменных, который при подстановке во все ограничения и граничные условия задачи обращает их в истинные числовые неравенства и равенства. Под областью допустимых решений (ОДР) задачи ЛП понимается геометрическое место точек, координаты которых являются допустимыми решениями.

Прежде всего, укажем в декартовой системе координат на рис.2.1 область допустимых решений для первого ограничения задачи (2.1). Для этого проведем в системе координат прямую, соответствующую первому ограничению. Уравнение этой прямой будет получено, если первое ограничение будет записано как равенство

0,8 x₁ + 0,5 x₂ = 400

Рис.2.1ОДР по молоку

Задавая произвольно значение одной из координат точки, лежащей на этой прямой, можно через полученное уравнение вычислить значение другой координаты этой же точки. Если данная прямая имеет точки пересечения с обеими осями в пределах создаваемого рисунка, то лучше присваивать нулевое значение сначала первой переменной, затем второй переменной, находя соответствующее значение другой переменной.

Результаты этих вычислений:

Отметим эти точки на осях рис.2.1 и проведем через них прямую, соответствующую первому ограничению. Если взять координаты любой точки, лежащей на этой прямой, то они обратят первое ограничение в равенство. Для выявления точек, координаты которых строго удовлетворяют данному ограничению, нужно указать на одну из образовавшихся полуплоскостей.

Для определения полуплоскости, координаты точек которой являются строгими решениями данного неравенства, необходимо выбрать пробную точку, явно принадлежащую какой-либо из двух полуплоскостей, полученных после проведения прямой, соответствующей этому неравенству.

Если координаты пробной точки обращают неравенство в истинное числовое неравенство, то полуплоскость, которой она принадлежит, является искомой. На рисунке 2.1 искомая полуплоскость выделена штриховкой.

Таким образом, с помощью одной пробы графически выявляется область допустимых решений для любого из ограничений и граничных условий анализируемой задачи ЛП.

Подобным образом следует поступить с каждым ограничением и граничным условием задачи ЛП (рис. 2.2).

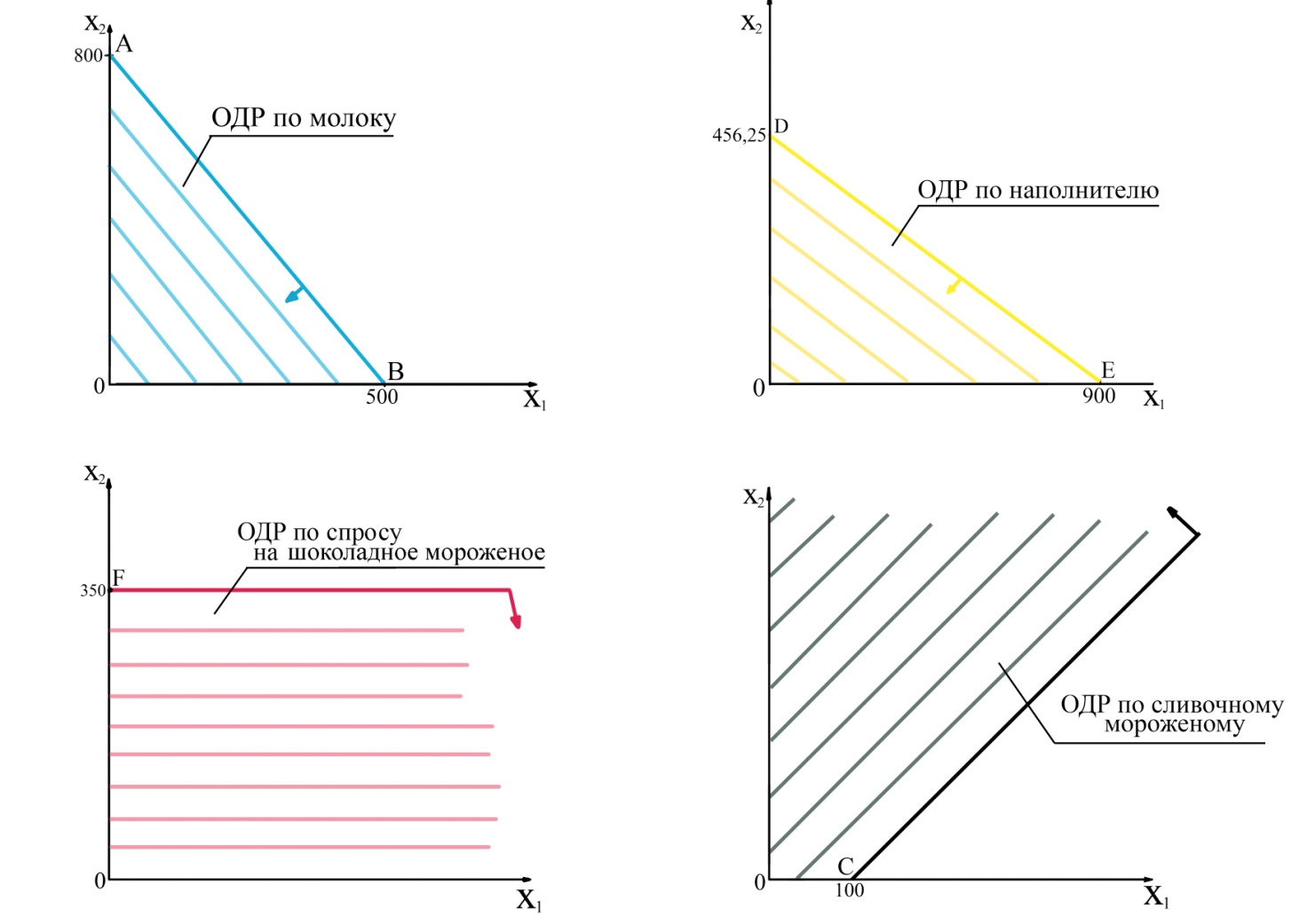
Рис.2.2. ОДР по ограничениям задачи

Следующим шагом нужно выделить общую часть обозначенных штриховкой полуплоскостей или, другими словами, найти их пересечение. На рисунке 2.3 заштрихованный многоугольник представляет собой все множество точек, координаты которых обращают в истинные утверждения все ограничения и граничные условия модели. Это означает, что область допустимых решений задачи ЛП построена.

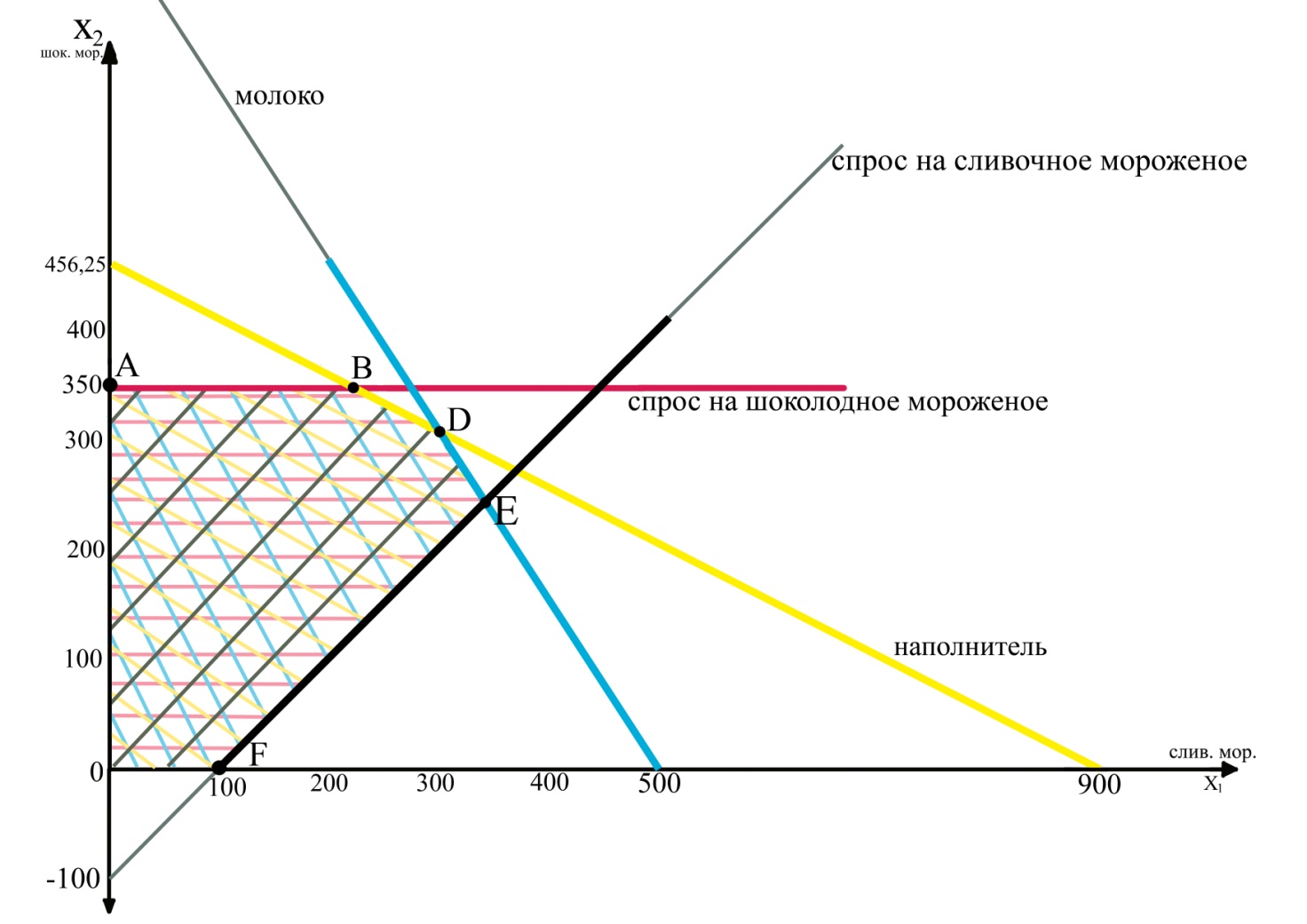
Рис.2.3 Нахождение общей ОДР задачи

Этап 2. Подоптимальным решением задачи ЛП понимается такое допустимое решение, при котором целевая функция задачи принимает экстремальное значение (максимальное или минимальное). Доказано, что среди множества оптимальных решений задачи ЛП, если они есть у этой задачи, обязательно существуют координаты вершины или угловой точки многоугольной области допустимых решений задачи ЛП (ограниченной или неограниченной). Набор числовых значений координат угловой точки ОДР называется опорным решением задачи ЛП. Другими словами, среди множества решений задачи ЛП всегда существует подмножество опорных решений.

Выделенному многоугольнику (рис. 2.4) области допустимых решений соответствуют шесть опорных решений – шесть угловых точек: О (0;0); А(0;350); В (212,5;350); Д (312,5;300); Е (346,15;246,15); F (100;0).

Координаты точки Д (312,5;300) можно найти, вычислив координаты точки пересечения прямых по молоку и наполнителю, для чего нужно решить систему уравнений:

откуда x₁ = 312,5; x₂ = 300.

Далее подставляем координаты каждой угловой точки в целевую функцию и определяем доход: А-4900; В-8300; Д-9200; Е-8984,5; F-1600.

Максимальный доход будет в точке Д, т.е. оптимальное решение состоит в выпуске 312,5 кг словочного мороженого и 300 кг шоколадного, при этом молоко и наполнитель использованы полностью, выполняются ограничения по спросу и достигается максимальный доход в 9200 руб.

Очевидно, что нахождение оптимального решения путем прямого набора их точек трудоемко, особенно когда много ограничений. Поэтому воспользуемся другим способом нахождения оптимума.

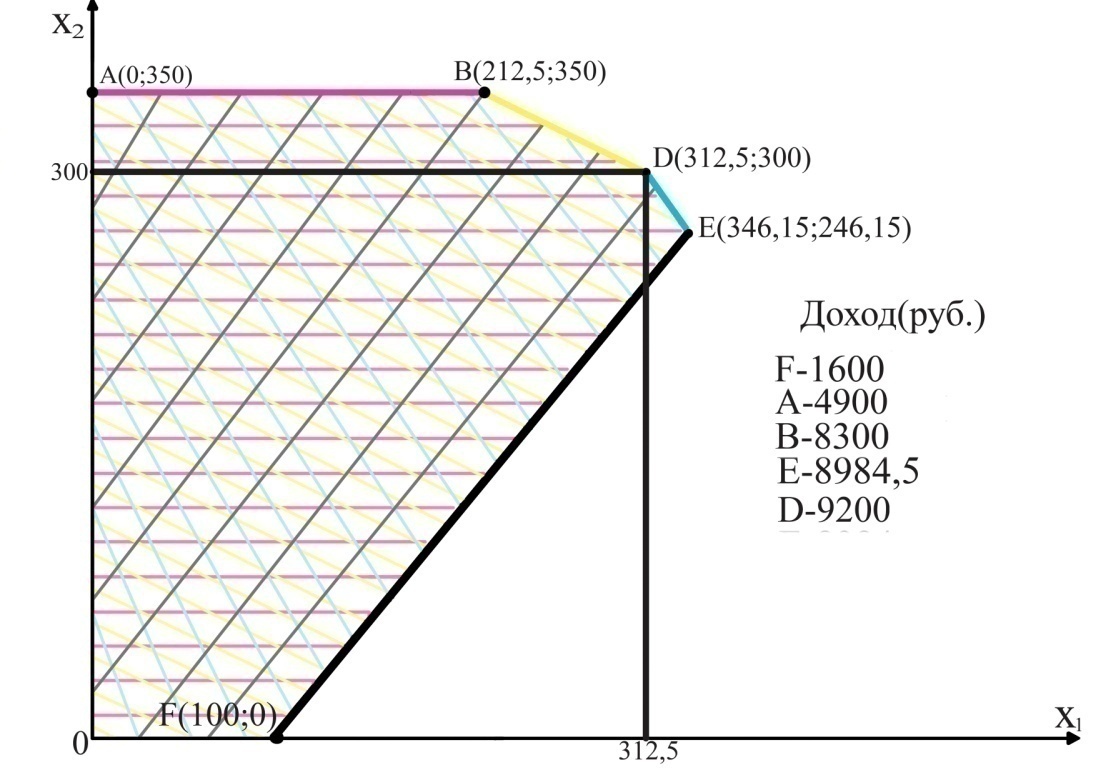
Рис.2.4 Нахождение оптимального решения

Этап 3-4. Для визуального выявления оптимального решения среди этих опорных решений используем следующие теоретические понятия.

Под линией уровня целевой функции понимается геометрическое место точек, для координат которых целевая функция имеет постоянное числовое значение (рис. 2.5).

Например, уравнение линии уровня 1600будет иметь вид: 16x₁+14₂=1600 или уравнение линии уровня 4900 - 16x₁+14x₂=4900 (соответственно: прямая 1)и 2),рис.2.5) и т.д.

Очевидно, что для всех возможных числовых значений линии уровня целевой функции являются прямыми, которые будут параллельные между собой и покрывать всю плоскость.

Под градиентом целевой функции понимается вектор с началом в текущей точки плоскости x=(x_1, x₂), координаты которого рассчитываются, как значение частных производных целевой функции F (х) в этой точке:

grad F(x)= ,

Градиент целевой функции обладает двумя характерными свойствами:

1) Перпендикулярен линиям уровня целевой функции;

2) Указывает направление наискорейшего роста целевой функции.

Используем изложенные выше теоретические положения для нахождения точки оптимального решения на построенной области допустимых решений. Второй точкой, через которую проходит F(x) является точка, координатами которой являются коэффициенты при неизвестных в целевой функции (x₁=16,x₂₌14) (первая точка для простоты - начало координат) (рис.2.5)

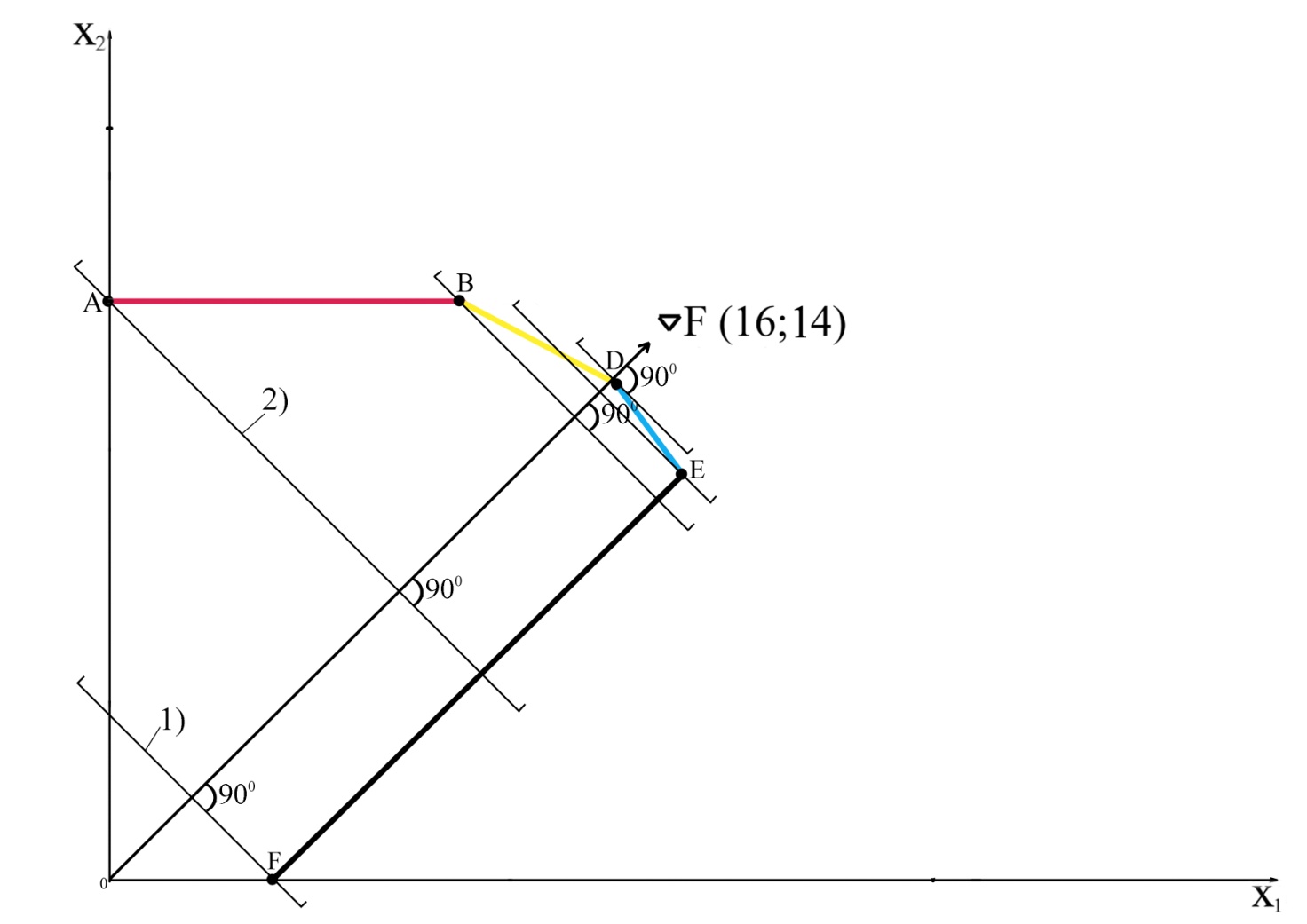
Рис.2.5 Нахождение оптимального решения с помощью линий прибыли и вектора-градиента

Этап 5. Определим наиболее удаленную в направлении градиента линию уровня, имеющую общую точку с областью допустимых решений. Такой линии уровня соответствует прямая, проходящая через точку ОДР с координатами (312,5; 300).

Отсюда оптимальным решением задачи являются: X₁=312,5; X₂=300; F(x)=9200 рублей.

Фирма выпускает два вида мороженого: сливочное и шоколадное. Для изготовления мороженого используются два исходных продукта: молоко и наполнители, расход которых на 1 кг мороженого и суточные запасы исходных продуктов даны в таблице 1.

Таблица 1.

Отпускная цена 1 кг сливочного мороженого 16 ден. ед., шоколадного – 14 ден. ед. Определите, какое количество мороженого каждого вида должна производить фирма, чтобы доход от реализации продукции был максимален?

Решение.

1. Экономическая постановка задачи: Определить оптимальный план производства мороженого, при котором затраты на производство мороженого были бы в пределах возможного максимального ресурсного обеспечения, а выручка фирмы – наибольшей.

2. Математическая модель:

Система функциональных ограничений:

3. Ввод исходных данных:

3.1. Создание экранной формы и ввод условия задачи Рис.1.

Рис. 1. Экранная форма задачи

ü В ячейках С8:D8 находятся значения коэффициентов целевой функции;

ü в массиве C6:C7 – коэффициенты левой части ограничений;

ü в столбце B6:B7- значения правой части ограничений.

ü Ячейки C2:D2 соответствуют переменным задачи (х₁, х₂).

ü В ячейке E9 будет отображаться значение целевой функции (Z).

3.2. Ввод зависимостей из математической модели в экранную форму.

Для нахождения целевой функции в ячейку E9 вводят формулу, по которой это значение рассчитывается (16х₁+14х₂).

Для этого в ячейку E9 введите функцию =СУММПРОИЗВ(C8:D8;C2:D2).

Ограничения: по молоку Е6=СУММПРОИЗВ(C6:D6;C2:D2), по наполнителям

ü Установить целевую ячейку - E9; Оптимизировать целевую функцию ячейка E9

ü Выбрать критерий оптимизации целевой функции (максимум, минимум, значение). В примере – максимум.

ü Поставить курсор в поле “Изменяя ячейки переменных” и ввести адрес массива, в котором находятся значения переменных. В примере – ячейки C2:D2;

ü Для введения соотношений между правыми и левыми частями ограничений нажмите кнопку “Добавить”. Откроется окно “Добавление ограничений.

ü В поле “Ссылка на ячейки:” введите адреса ячеек левой части ограничений - Е6:Е7. В поле знака выберите <=.

ü В поле “Ограничение:” введите адрес ячеек правой части ограничений - B6:B7.

Выберите метод решения «Поиск решения нелинейных задач методом ОПГ»

В окне “Результаты поиска решения” представлены типы отчетов “Результаты”, “Устойчивость”, “Пределы”. Они необходимы при анализе полученного решения на чувствительность Рис. 2.

Рис. 2. Окно “Результаты поиска решения”

В экранной форме появится оптимальное решение задачи.

Рис. 3. Экранная форма задачи после получения оптимального решения с дополнительным форматированием ячеек С2:D2, B6:E6, B7:E7, C8:D8, E9.

Выводы. Итак, оптимальный план производства сливочного мороженого – х₁=312,5 кг, шоколадного мороженого – х₂=300 кг, значение выручки при этом составит Z=9200 ден. ед. (рис. 3). При этом все ресурсы (молоко и наполнители) будут использованы в полном объеме. При необходимости можно создать отчет о результатах Рис. 4.

Среди множества задач оптимизации особую роль в силу своей практической значимости играют задачи линейного программирования. Одной из распространенных задач является задача на оптимальное использование ресурсов. Рассмотрим задачу на оптимальный выпуск мороженного и дадим экономический анализ решения на устойчивость.

Фирма выпускает два вида мороженого: сливочное и шоколадное. Для изготовления мороженого используются два исходных продукта: молоко и наполнители, расходы которых на 1 кг мороженого и суточные запасы даны в таблице.

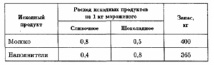
Изучение рынка сбыта показало, что суточный спрос на сливочное мороженое превышает спрос на шоколадное не более чем на 100 кг. Кроме того, установлено, что спрос на шоколадное мороженое не превышает 350 кг в сутки. Розничная цена 1 кг сливочного мороженого 16 р., шоколадного – 14 р. Какое количество мороженого каждого вида должна производить фирма, чтобы доход от реализации продукции был максимальным?

Целевая функция будет иметь вид

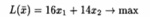
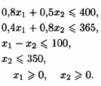
Решив задачу графически находим оптимальное решение: xопт=(312,5;300) Фирма должна выпускать в сутки 312,5 кг сливочного мороженного и 300 кг шоколадного.

Проведем экономический анализ рассмотренной выше задачи:

Рассмотрим увеличение ресурса по молоку. Получим предельно допустимый суточный запас молока: = 432,1 кг. Предельно допустимый суточный запас наполнителей можно увеличивать до значения 392,5 кг. Не изменяя оптимальное решение правую часть ограничения можно уменьшать до величины 312,5–300=12,5 кг.

При неизменном оптимальном решении разница в покупательском спросе на сливочное и шоколадное мороженое может изменяться в диапазоне от 12,5 до 500 кг.

Читайте также: