Как сделать треугольник паскаля в эксель

Обновлено: 07.07.2024

Цель: ознакомиться с треугольником Паскаля как с разновидностью треугольников, изучить свойства арифметического треугольника, рассмотреть применение треугольника в разных сферах жизни, узнать более обширную и подробную информацию о числовой таблице, а также выявить связь треугольника Паскаля с числами Фибоначчи и биномиальными коэффициентами.

Задачи: изучить литературу по теме «Треугольник Паскаля», выявить свойства чисел, входящих в состав арифметического треугольника, определить применение свойств чисел треугольника Паскаля, сформулировать вывод и итоги исследования.

Актуальность данной работы обусловлена широким интересом к теме «Треугольник Паскаля» в современной науке, а также ее недостаточной разработанностью. Данная работа позволяет выявить, насколько широко применяются треугольники в практической жизни, и какую они играют роль в различных направлениях.

Предмет исследования: свойства треугольника Паскаля.

Мой личный вклад в работу состоит в отслеживании свойств арифметического треугольника в школьных учебниках, материалах ГИА и ЕГЭ, а также дополнительной литературе.

Практическое значение работы: материалы данной работы могут быть использованы в качестве дополнительного материала на уроках алгебры и геометрии как в обычных, так и в профильных классах.

Выводы: таким образом, я познакомилась с треугольником Паскаля как с разновидностью треугольников, изучила свойства арифметического треугольника, выяснила какая же связь существует между числами Фибоначчи и биномиальными коэффициентами, рассмотрела его применение в решении некоторых задач.

Блез Паскаль – французский математик…………………………………….7

Треугольник Паскаля как разновидность треугольников…………………8

Свойства арифметического треугольника ………………………………. 12

Исследование теории вероятности и последовательности чисел Фибоначчи. Биномиальные коэффициенты. Примеры решения задач с использованием свойств арифметического треугольника

2.1. Связь треугольника Паскаля с теорией вероятности………………………15

2.2. Закономерности в последовательности ряда чисел Фибоначчи…………..17

2.3. Биномиальные коэффициенты и их применение в различных областях математики…………………………………………………………………………. 18

Методы решения задач по теме «Треугольник Паскаля»

3.1. Составление последовательности тренировочных задач по теме «Треугольник Паскаля» ………………………………………………………………………………………..21

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ……………………..………23

Тема моей работы звучит так: «Удивительный треугольник Паскаля».

Объектом исследования является треугольник Паскаля как таблица коэффициентов.

Предметом исследования являются свойства треугольника Паскаля.

Целью работы является ознакомление с треугольником Паскаля как с разновидностью треугольников, изучение свойств треугольника Паскаля, рассмотрение применения арифметического треугольника в разных сферах жизни, выявление связи треугольника с биномиальными коэффициентами и числами Фибоначчи.

Актуальность данной работы обусловлена широким интересом к теме «Треугольник Паскаля» в современной науке, а также ее недостаточной разработанностью. Данная работа позволяем выявить насколько широко применяется арифметический треугольник в математике.

Задачами исследования является изучение литературы по теме «Треугольник Паскаля», выявление свойств чисел, входящих в состав арифметического треугольника, определение применения свойств чисел треугольника Паскаля, формулирование вывода и подведение итогов исследования.

Для достижения поставленной цели и задач необходимо решить следующие задачи:

Изучить статьи и учебно-методическую литературу по данной теме.

Проанализировать действующие учебники, содержащие материалы по данной теме.

Рассмотреть основные методы и приемы решения задач по теме «Треугольник Паскаля» .

Два года назад произошло наше увлекательное знакомство с таинственным и загадочным миром геометрии. Одной из глав курса геометрии 7 класса называется «Треугольники». Меня очень заинтересовала данная тема. Я всегда хотела узнать много нового о треугольниках. Ведь мир треугольников очень удивителен и интересен. Я хочу узнать как можно больше о происхождении треугольников, об их значении в нашей жизни.

Треугольник - первая геометрическая фигура, встречающаяся в древних орнаментах. Изучая литературу, я узнала, что у разных народов и в разные времена он служил для воплощения возвышенных образов природы и природных сил в простые и загадочные символы. Например, в Египте он символизировал триаду духовной воли, любви, интуиции и высшего разума человека, то есть его личность или душу. Треугольник с горизонтальной чертой считается пассивным и означает воздух, умеренный огонь, соответствующий синему цвету. Перевернутый треугольник означает чашу, готовую принять воду; мудрость, порождающую главную идею; зеленый цвет. Треугольник воздуха с горизонтальной чертой символизирует Землю, неподвижную стоячую воду и соответствует черному цвету. Ацтеки использовали изображение треугольника с вершиной наверху, соединенного с перевернутым треугольником, в качестве символа временного цикла. Треугольник в сочетании с крестом образует алхимический знак Серы. Равносторонний треугольник, символизирующий, по древнееврейской традиции, совершенство, у христиан означает Троицу - Отца, Сына и Святого Духа.

Когда я подробно познакомилась с треугольником Паскаля, большим открытием для меня оказалось, что это и не совсем треугольник в привычном для нас представлении. Это скорее таблица с интересной структурой, простой и совершенной, содержащая числа – коэффициенты. Поскольку числа данного треугольника обладают особыми свойствами, то сам треугольник Паскаля можно считать универсальным математическим инструментом. Именно это и является гипотезой моего исследования.

Блез Паскаль – французский математик

Блез Паскаль (19 июня 1623, Клермон-Ферран, — 19 августа 1662, Париж) — французский математик, физик, литератор, философ, один из основателей математического анализа, теории вероятностей и проективной материи. Паскаль был первоклассным математиком. Он помог создать два крупных новых направления математических исследований. Его удобное представление биномиальных коэффициентов в виде таблицы, изложенное в «Трактате об арифметике треугольника», увидевшем свет в 1653 г., (на тот момент Блезу Паскалю было шестнадцать лет ), получит название «треугольника Паскаля». Кроме того, Паскаль открыл и исследовал алгебраическую кривую, с тех пор получившую название «улитка Паскаля». Переписка французского математика с Пьером де Ферма по теории вероятностей впоследствии оказало принципиальное влияние на развитие современной экономики.

Треугольник Паскаля как разновидность треугольников

Изучая литературу, я выяснила, что треугольник Паскаля — арифметический треугольник, образованный биномиальными коэффициентами и назван в честь великого французского математика Блеза Паскаля. В действительности, треугольник Паскаля был известен задолго до 1653 года, что является датой выхода "Трактата об арифметическом треугольнике". Так, этот треугольник воспроизведен на титульном листе учебника арифметики, написанном в начале XVI Петром Апианом, астрономом из Ингольтштадского университета. Изображен такой треугольник и на иллюстрации в книге одного китайского математика, выпущенной в 1303 году. Омар Хайям, бывший не только философом и поэтом, но и математиком, знал о существовании треугольника около 1100 года, в свою очередь, заимствовав его из более ранних китайских или индийских источников.

Из книги "Математические новеллы" (М., Мир, 1974) Мартина Гарднера я хотела бы привести его высказывание: "Треугольник Паскаля так прост, что выписать его сможет даже десятилетний ребенок. В тоже время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд между собой ничего общего. Столь необычные свойства позволяют считать треугольник Паскаля одной из наиболее изящных схем во всей математике"

Я рассмотрела схему построения треугольника, предложенную Гуго Штейнгаузом в его классическом «Математическом калейдоскопе»: предположим, что вы входите в город как показано на схеме синей стрелкой, и можете двигаться только вперед, точнее, все время выбирая, вперед налево, или вперед направо. Узлы, в которые можно попасть только единственным образом, отмечены зелеными смайликами, точка, в которую можно попасть двумя способами, показана красным смайликом, а тремя, соответственно - розовыми. Это один из вариантов построения треугольника.

Этим фактом и воспользуемся. Только в Excel удобней использовать не классический (построчный) вид треугольника Паскаля, а такой:

Здесь биномиальные коэффициенты выписаны по диагонали, в первой заполненной строке и первом заполненном столбце единицы, а в остальных сумма вехнего и левого элемента.

Перейдем к построению. Для нас достаточно выписывать не коэффициенты, а только их четность.

Для начала сделаем размер ячеек в Excel, к примеру 7 на 7 пикселей.

Станем в ячейку B2, затем выделим область B2:DY129 — для этого нажимаем Ctrl + G и в поле ссылка пишем B2:DY129.

Теперь в строке формул пишем =ЕСЛИ(ИЛИ(СТРОКА()=2;СТОЛБЕЦ()=2);1;ОСТАТ(A2+B1;2))

и нажимаем Ctrl + Enter, чтобы заполнить подобной формулой всю выделенную область.

Заходим Меню — Условное форматирование и для значения 1 указываем цвет ячейки.

В итоге получаем:

Следует отметить, что треугольник Серпинского получается при некоторой разновидности случайного блуждания на плоскости. А именно:

Зафиксируем на плоскости 3 вершины треугольника и возьмем еще одну точку.
Первую точку получим как середину отрезка между случайно выбранной вершиной и точкой из п.1.
Вторую точку получим как середину отрезка между случайно выбранной вершиной и первой точкой.
…
Повторяем процесс много раз.

Можно ипользовать такой макрос:

Public Sub Макрос()

Dim arRange(1 To 3) As Range

Dim tekRow As IntegerDim tekColumn As IntegerDim i As IntegerDim iT As Integer
tekRow = Int(1000 * Rnd) + 1

tekColumn = Int(200 * Rnd) + 1
Set arRange(1) = Cells(1, 1)

Set arRange(2) = Cells(50, 250)Set arRange(3) = Cells(200, 20)
Cells.Clear

For i = 1 To 20000

iT = (Int(1000 * Rnd) Mod 3) + 1 tekRow = Int((tekRow + arRange(iT).Row) / 2) tekColumn = Int((tekColumn + arRange(iT).Column) / 2) Cells(tekRow, tekColumn).Interior.ColorIndex = 5Next
End Sub

Сначала запишите число 1.

Поместите еще две единицы, чтобы начать построение следующей строки.

Теперь вам нужно узнать, как построить нижележащие строки, следующие за двумя первыми, содержащими только единицы. В каждой новой строке количество элементов будет на один больше, чем в предыдущей. Каждая строка начинается и заканчивается числом 1.

Найдите внутреннее число, используя числа, расположенные выше него. Каждый внутренний элемент может быть вычислен путем сложения двух чисел, расположенных выше него. Например, в середине третьей строки мы помещает число 2 (1+1=2).

По мере заполнения строк треугольника, вы сможете заметить множество интересных свойств треугольника Паскаля.

Первое и последнее число в каждой строке равны 1. Второе и предпоследнее — натуральные числа, третье в строке — треугольное число.
Сумма чисел каждой строки (номер строки указан) равна числу 2, возведенному в степень, равную номеру этой строки (основание степени равно 2).
Принимая во внимание, что первое число в каждой строке является нулевым элементом и равно 1, если вы возьмете следующее число в ряду и разделите все другие элементы в этой строке, вы увидите, что все элементы нацело делятся на номер данной строки.
За исключением некоторых случаев, каждая линия в треугольнике Паскаля имеет прямой эффект, который проявляется при возведении любого основания в степень, соответствующую номеру строки. В некоторых строках, где следующая ячейка содержит одно или больше чисел на ячейку, разряд десятков суммируется с числом в ячейки слева.
Треугольник Паскаля симметричен..

Наименование:

Информация:

Описание (план):

С одним из видов числовой последовательности мы встречаемся в биологии. Число образовавшихся клеток при митозе и мейозе изменяется как n-й член геометрической прогрессии со знаменателем 2 и 4 соответственно. В литературе, при изучении стихотворных метров, на помощь приходит арифметическая прогрессия. Например, ямб – стихотворный метр с акцентами на чётных слогах стиха. Номера ударных слогов (второй, четвёртый, шестой, восьмой и т. д.) образуют арифметическую прогрессию с первым членом два и разностью, равной двум. Числовые последовательности нашли своё применение и в экономике. Так, при подсчёте банковского процента нам помогает арифметическая и геометрическая прогрессии. Если смотреть на листья растения сверху, можно заметить, что они распускаются по спирали. Углы между соседними листьями образуют правильный математический ряд, известный под названием последовательности Фибоначчи. Благодаря этому каждый отдельно взятый лист, растущий на дереве, получает максимально доступное количество тепла и света. В природе последовательность Фибоначчи можно проследить на примерах спирального развития сегментов раковины и лепестков подсолнуха, расходящихся лучами из одной точки в центре цветка. в строении нашего тела, в ботанике, в процессах квантовой механики, в практической деятельности людей, она нашла широкое научное применение в математике, технике, музыке, эстетике и пр.
В своей курсовой работе я приведу примеры использования программных средств компьютера при работе с числовыми последовательностями.

Фигурные числа в треугольнике Паскаля.

В математике существует множество последовательностей, упакованных в одну форму. Примером может являться треугольник Паскаля.
Треугольник Паскаля часто записывают в виде равнобедренного треугольника, в котором на вершине и по боковым сторонам стоят единицы, каждое из остальных чисел равно сумме двух чисел, стоящих над ним слева и справа в предшествующей строке. Треугольник можно продолжать неограниченно. Он обладает симметрией относительно вертикальной оси, проходящей через его вершину.

Треугольник Паскаля прост, но в то же время таит в себе неисчерпаемые сокровища и связывает воедино различные разделы математики, не имеющие на первый взгляд ничего общего. Отметим лишь некоторые из основных свойств.
Каждый элемент является биномиальным коэффициентом. Именно это фундаментальное свойство треугольника Паскаля связывает его не только с комбинаторикой и теорией вероятностей, но и другими областями математики и ее приложений, вдоль диагоналей, параллельных сторонам треугольника, выстроены треугольные числа и их обобщения на случай пространств всех размерностей.
В этой части курсовой работы поставлена следующая задача: задать треугольник Паскаля с помощью Microsoft Office Excel и показать ряд интересных свойств этого треугольника.
Для этого в столбце А укажем номер строки треугольника: строки нумеруются сверху вниз, начиная с нуля. В столбец В заполним нулями. Вершина треугольника находится в ячейке С1, значение которой равно 1. С помощью сложения двух соседних элементов предыдущей строки заполняем строку 2(к=1). Для этого в ячейку С2 записываем формулу вычисления В1+С1 и переносим ее на соседнюю ячейку.

Растянув формулы по строкам и столбцам получаем треугольник Паскаля:

Пользуясь возможностями Excel, не проводя вычислений, рассмотрим некоторые свойства треугольника Паскаля. Рассмотрим значения треугольника находящиеся в столбцах. Очевидно, что столбец D содержит натуральный ряд. Столбец Е – ряд треугольных чисел. Покажем это.
Треугольное число — это число кружков, которые могут быть расставлены в форме равностороннего треугольника.

Последовательность треугольных чисел Тn для n = 0, 1, 2, … начинается так:
0, 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, …
n-ый член последовательности треугольных чисел можно задать так: Tn=1+2+3+…+n
Покажем, что в треугольнике Паскаля действительно есть последовательность треугольных чисел:
Tn=E(n+1)=D(n)+E(n)= D(n)+ D(n-1)+E(n-1)=…=
=Dn+D(n-1)+…+D1+E1=0+1+2+…+n-2+n-1+n.
Так как ряд начинается с ячейки E2 со значением 0, то для шестого члена последовательности имеем: T6=E7=1+2+…+6=15.
Соседний столбец, столбец F заполнен элементами последовательности тетраэдрических чисел Sn: 0,1,4,10, 24,36,… Эти числа показывают, сколько шаров может быть уложено в виде треугольной пирамиды (тетраэдра).

Известно, что каждый член этой последовательности может быть описан с помощью треугольных чисел: Sn= T1+T2+…+Tn. Действительно, геометрически это можно показать так:

В нашем случае элемент Sn расположен в ячейке по адресу F(n+2)=E(n+1)+F(n+1)=E(n+1)+En+Fn=…=E(n+1)+En+…+E2= Tn+Tn-1+…+T1
Есть еще одна последовательность фигурных чисел, которая может быть выражена с помощью треугольных чисел: квадратная. Kn=Tn+Tn-1. Элементы этой последовательности найдем с помощью Exsel. Задав для элементов столбца F формулу Fn=En+E(n-1) получаем элементы последовательности квадратных чисел.

Геометрически такие числа могут быть представлены в виде площади квадрата с целочисленной стороной.

Пространственно из этих чисел получаются пирамиды с четырехугольником в основании.

Назовем последовательность таких чисел пирамидальной-4 Pn. Приведем пример:

Pn=K1+K2+…+Kn=T1+(T1+T2)+(T2+T3)+…+(Tn-2+Tn-1)+(Tn-1+Tn)+Tn=
=(T1+T2+…+Tn-1)+(T1+T2+…+Tn-1+Tn)=Sn-1+Sn
Итак, представим в Excel все разобранные выше последовательности фигурных чисел.

Изучение элементов теории фигурных чисел на занятиях по математике в старших классах средней школы не только возможно, но и крайне желательно: обширный исторический материал, расцвеченный увлекательными легендами и мифами, способствует повышению интереса к предмету, интересные геометрические конструкции выполняют пропедевтическую роль, готовя старшеклассников к изучению современной дискретной математики, в частности теории графов.
Задание треугольника Паскаля в Excel делает доступным мгновенное вычисление любого элемента, позволяет убедиться во множестве его свойств.

Узоры таблицы Пифагора

Впервые таблица Пифагора примерно в том же виде, в каком ее печатают на обложках школьных тетрадей, но в ионийской нумерации, появилась в сочинении неопифагорейца Никомаха Геразского (I-II вв. н. э.) «Введение в арифметику». По словам Никомаха, эта таблица восходит «к самому Пифагору». Еще более древние таблицы умножения обнаружены на месопотамских глиняных табличках — их «возраст» около 5 тысяч лет. Таблицу Пифагора можно расширять вправо и вниз до бесконечности, соблюдая единственное условие: каждое число таблицы есть произведение номера строки и номера столбца, в которых оно стоит.
Расширенные таблицы умножения существуют давно. Так, например, в первой печатной математической книге на русском языке «Считание удобное, которым всякий человек, купующий или продающий, зело удобно изыскати может число всякие вещи» (Москва, 1682) имеется таблица умножения чисел от 1×1 до 100×100.
Таблица умножения скрывает в себе много замечательных математических закономерностей, поиск которых способен превратиться в увлекательное занятие, сулящее немало сюрпризов.
К изучению свойств расширенной таблицы Пифагора можно привлечь компьютер. Каждое число таблицы изобразим точкой (или клеткой) координатной плоскости монитора и в соответствии со свойствами чисел окрасим точки каким-либо цветом. Это реализуется с помощью шаблона программы, написанной на языке Turbo Basic version 1.1.
screen 12
for n=1 to 120
for m=1 to 120
p=m*n
line (4*n,4*m)-(4*n+2,4*m+2),15,bf
if условие then line (4*n,4*m)-(4*n+2,4*m+2),1,bf
next m,n
При исполнении программы каждое число p расширенной таблицы Пифагора 120×120, находящееся на пересечении n-го столбца и m-й строки, будет изображаться белой клеткой, а числа, удовлетворяющие заданному в программе условию, — синими.
Так, на рис. 1 (программа 1) синим цветом выделены квадратные числа таблицы Пифагора: 1, 4, 9, 16, …, n2,… , зеленым — треугольные: 1, 3, 6, 10, …, 1/2 n(n+1),… красным — числа одновременно и квадратные и треугольные: 1, 36, 1225, 41616 и т.д.
Чтобы получить представление о том, как в таблице Пифагора расположены числа, дающие одинаковые остатки при делении, например на 5, закрасим числа, дающие остатки 0, 1, 2, 3, 4, каждое своим цветом. Как это ни удивительно, но таблица Пифагора оказывается расчленен ной на совершенно одинаковые по раскраске квадраты (рис. 2, программа 2).
Аналогичное разбиение получается при делении чисел таблицы на любое другое натуральное число k, в чем легко убедиться, заменив в программе число 5 на него.
Благодаря свойству периодичности таблицы Пифагора по остаткам на экране возникают разнообразные мозаики. Очевидно, чем больше k, тем больше будет остатков r, тем больше потребуется цветов. Чтобы узоры не были слишком пестрыми, ограничимся, например, тремя цветами. Для этого остатки сгруппируем по модулю 3, то есть первым цветом закрасим числа таблицы с остатками 1, 4, 7, 10. вторым — числа с остатками 2, 5, 8, 11. а третьим — числа, кратные 3 (рис.3, программа 3).
Можно расчленить любую из этих мозаик на три одноцветные, дополняющие одна другую до полной мозаики. Каждая из них в отдельности тоже представляет интерес (рис.4, программа 4).
Еще один вариант трехцветных мозаик приведен на рис. 5 (программа 5). Здесь для большей симметрии одинаковым цветом закрашены не только числа с одинаковым остатком r, но и числа с остатком, дополняющим r до k.
Интересные мозаики возникают и тогда, когда красят не все числа, а выборочно. Например, трехцветный узор на рис. 6 (программа 6). Кружевной монохромный узор (рис.7, программа 7) возникает, если во всей таблице закрасить одинаковым цветом только числа, дающие остатки, сравнимые с одним и тем же натуральным числом.
А если в программу включить генератор случайных чисел для определения размеров квадратов k, лежащих в периоде номеров расширенной таблицы Пифагора и номеров цвета c, то с помощью компьютера таблица превратится в своеобразный калейдоскоп удивительных и неповторяющихся узоров (рис. 8, программа 8).
На рис. 9 (программа 9) показано, как в таблице Пифагора 32×32 чередуются числа нечетных и четных сотен. Здесь каждое число изображено клеткой синего или зеленого цвета. Причем числа первой, третьей, пятой и т. д. сотни закрашены синим, а числа второй, четвертой, шестой и т.д. — зеленым. Ясно, что если произведение n x m постоянно, то между числами существует обратная пропорциональность, поэтому чередующиеся синие и зеленые полосы имеют гиперболическую форму.
С увеличением произведения n x m ширина полос уменьшается, а затем полосы и вовсе разрываются и распадаются на одноцветные островки, которые группируются с островками того же цвета, но из другой сотни, образуя симметричные формы (рис. 10, программа 10). Здесь каждое число таблицы 480×480 изображено точкой-пикселем.
Занимаясь изучением свойств таблицы Пифагора, можно отыскать новые, не менее красивые узоры на основе этой древней числовой схемы.

* Примечание. Уникальность работы указана на дату публикации, текущее значение может отличаться от указанного.

Комбинаторика — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения элементов) и отношения на них. Термин комбинаторика был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве». Excel поддерживает ряд функций комбинаторики. Чтобы разобраться, какую формулу использовать, следует ответить на ряд вопросов:

Исходное множество содержит только уникальные элементы, или некоторые из них могут повторяться?
Операция выполняется со всеми элементами множества, или только с некоторой выборкой из них?
Важен ли порядок элементов в выборке?
После выбора элемента мы его возвращаем назад?

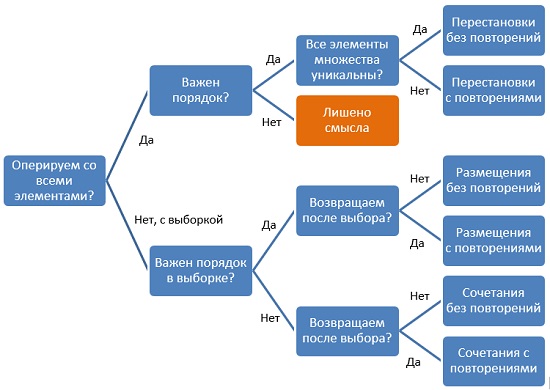
Рис. 1. Дерево решений, какую формулу комбинаторики использовать

Перестановки без повторений

Возьмем несколько различных элементов (предметов) и будем переставлять их всевозможными способами, оставляя неизменным их число и меняя только их порядок (рис. 2). Каждая из получившихся таким образом комбинаций носит название перестановки. Перестановкой из n элементов называется упорядоченное множество, составленное из всех элементов множества.

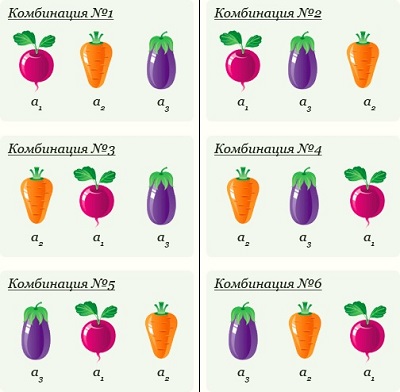
Рис. 2. Перестановки (картинка взята здесь)

Если все n элементы разные, то число перестановок обозначается P_n от perturbation.

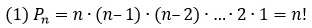
С другой стороны, произведение n первых натуральных чисел называется n-факториал и обозначается n!

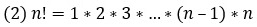
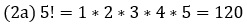
По определению: 1! = 1; 0! = 1.

Функция в Excel =ФАКТР(n). Факториал растет очень быстро. Существенно быстрее экспоненты (рис. 3).

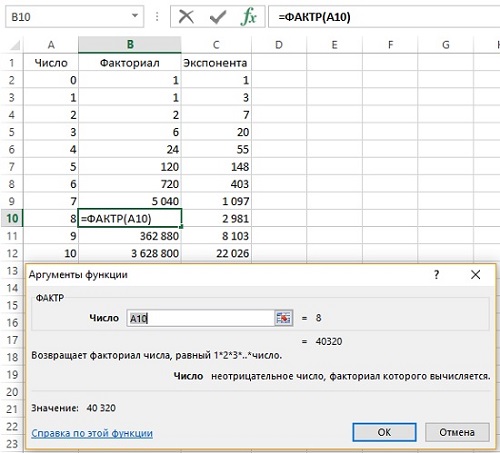
Рис. 3. Расчет числа перестановок без повторений с помощью факториала

Перестановки с повторениями

Если в основном n множестве не все элементы разные, то число перестановок будет меньше n! Например, если наше множество состоит из трех яблок и одной груши, то всего возможно 4 перестановки (рис. 4). Груша может быть первой, второй, третьей или четвертой, а яблоки неразличимы).

Рис. 4. Перестановки с повторениями (картинка найдена здесь)

В общем случае, можно сказать: последовательность длины n, составленная из k разных символов, первый из которых повторяется n₁ раз, второй – n₂ раз, третий – n₃ раз, …, k-й – n_k раз (где n₁ + n₂ + … + n_k = n) называется перестановкой с повторениями из n элементов.

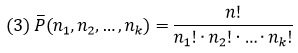
Пример. Сколько различных пятибуквенных слов можно составить из букв слова «манна»?

Решение. Буквы а и н повторяются 2 раза, а буква м один раз.

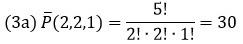
Размещение без повторений

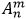
Размещением из n элементов по m называется упорядоченный набор из m различных элементов, выбранных из n-элементного множества (все элементы множества уникальны; позиции элементов в выборке важны). Число размещений обозначается от arrangement.

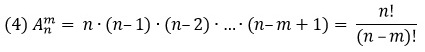
Например, два элемента из трех можно выбрать и расположить шестью способами (рис. 4):

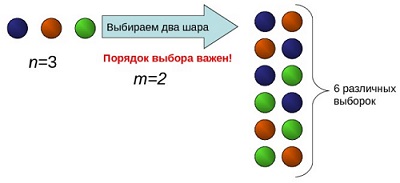
Рис. 5. Размещение без повторений (картинка из презентации)

Если m = n количество элементов совпадает с количеством имеющихся мест для размещения. Знаменатель в формуле (4) превращается в 0! = 1. Остается только числитель n! А это – изученная выше перестановка без повторений; см. формулу (1).

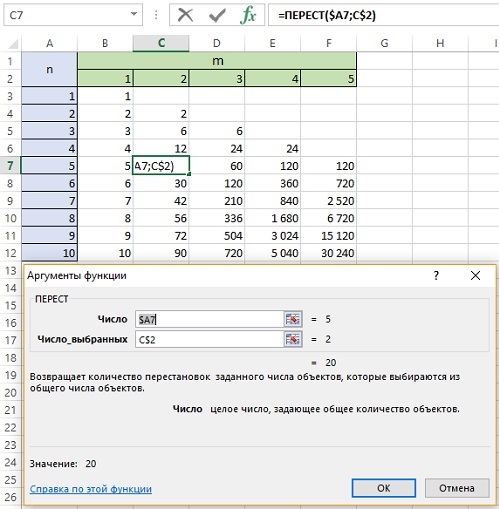
Рис. 6. Размещение без повторений; обратите внимание на смешанные ссылки, которые позволяют протянуть формулу на всю таблицу

Размещение с повторениями

Размещение с повторениями по смыслу отличается от перестановок с повторением. Перестановки с повторением – это операция над множеством, которое состоит из нескольких видов элементов, так что каждый вид представлен несколькими одинаковыми элементами. Размещение с повторениями – выборки из множества с возвращением выбранного элемента назад перед каждым новым выбором.

Например, если у вас множество, включающее грушу, яблоко и лимон, и вам нужно выбрать два элемента, так что после первого выбора вы возвращаете выбранный предмет назад, то существует девять различных комбинаций (рис. 7).

Рис. 7. Размещение с повторениями

В общем случае размещение с повторениями или выборка с возвращением – это размещение «предметов» в предположении, что каждый «предмет» может участвовать в размещении несколько раз. По правилу умножения количество размещений с повторениями из n по k:

В Excel используется функция ПЕРЕСТА(n;k).

Задача. Сколько различных номеров можно составить в одном коде региона?

Подсказка. В номере используется 12 букв алфавита, также существующих и в латинском алфавите (А, В, Е, К, М, Н, О, Р, С, Т, У, Х).

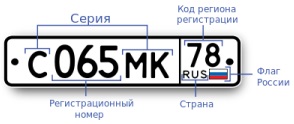
Решение. Можно воспользоваться формулой для размещения с повторениями:

Каждую цифру можно выбрать 10 способами, а всего цифр 3, при этом они могут повторяться, и их порядок важен. Каждую букву можно выбрать 12 способами, при этом буквы могут повторяться, и их порядок важен.

Сочетания без повторений

Сочетаниями из n множества по m элементов называются комбинации, составленные из данных n элементов по m элементов, которые различаются хотя бы одним элементом (в сочетаниях не учитывается порядок элементов).

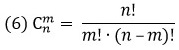
Например, два элемента из 4 сочетаются 6 способами (порядок следования не важен):

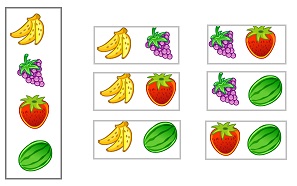
Сочетания без повторений образуют знаменитый треугольник Паскаля (рис. 10). В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Числа в строках, составляющие треугольник Паскаля, являются сочетаниями

где n – номер строки, m – номер элемента в строке, начиная с нулевого. Например, в строке 7:

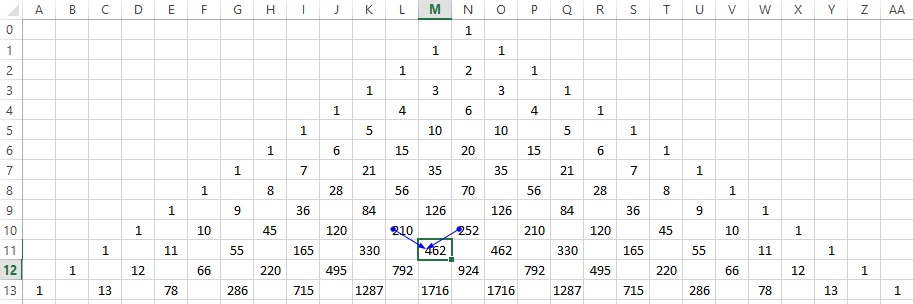
Рис. 10. Треугольник Паскаля; чтобы увеличить изображение кликните на нем правой кнопкой мыши и выберите Открыть картинку в новой вкладке

В Excel используется функция =ЧИСЛКОМБ(n;m).

Сочетания с повторениями

Сочетания с повторениями по смыслу похожи на размещение с повторениями – это выборки из множества с возвращением выбранного элемента назад перед каждым новым выбором. При этом порядок в выборке не важен.

Например, два предмета из четырех можно выбрать 10 способами, если после каждого выбора предмет возвращается назад (рис. 11).

В общем случае, число сочетаний с повторениями:

Для нашего примера с фруктами

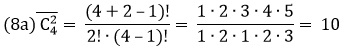
В Excel для подсчета числа сочетаний с повторениями используется функция =ЧИСЛКОМБА(n;m). В нашем примере =ЧИСЛКОМБА(4;2) = 10.

1 комментарий для “Комбинаторика в Excel”

Спасибо большое за понятное и наглядное изложение этой сложной темы! Не в первый раз Ваши публикации выручают меня, это просто энциклопедия полезнейшего контента!

Построить спираль Архимеда по следующим данным:
- в столбце А – значения угла t в радианах от 0 до 10 с шагом 0,2
- в столбце В – значения r = 0,5* t
- в столбце С – значения х = r * cos ( t )
- в столбце D – значения y = r * sin ( t )
- выделить значения в столбцах С и D и построить диаграмму
(тип: точечная с гладкими кривыми )

Построить астроиду по следующим данным:
- в столбце А – значения угла t в радианах от 0 до 7 с шагом 0,2
- в столбце В – значения х = 2*( cos ( t )) 3
- в столбце С – значения y = 2*( sin ( t )) 3
- выделить значения в столбцах B и С и построить диаграмму
(тип: точечная с гладкими кривыми )

Построить улитку Паскаля по следующим данным:
- в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
- в столбце В – значения t = a * π/180 (угол в радианах)
- в столбце С – значения p = cos ( t )–0,5
- в столбце D – значения x = p * cos ( t )
- в столбце Е – значения у = p * sin ( t )
- выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми )

Построить лемнискату Бернулли по следующим данным:
- в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
- в столбце В – значения t = a * π/180 (угол в радианах)
- в столбце С – значения r = 2* sin (2* t ) 2
- в столбце D – значения x = r * cos ( t )
- в столбце E – значения y = r * sin ( t )
- выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми )

Построить график в форме сердца по следующим данным:
- в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
- в столбце В – значения t = a * π/180 (угол в радианах)
- в столбце С – значения x = 16*( sin ( t )) 3
- в столбце D – значения у =13* cos ( t )–5* cos (2* t )–2* cos (3* t )– cos (4* t )
- выделить значения в столбцах C и D и построить диаграмму
(тип: точечная с гладкими кривыми )

Читайте также: