Решение двойственной задачи в excel поиск решения

Обновлено: 04.07.2024

Целью работы является приобретение навыков построения математических моделей двойственных задач линейного программирования и их решения в среде Microsoft Excel.

Порядок выполнения лабораторной работы

Для выполнения лабораторной работы необходимо:

1) повторить теоретический материал, относящийся к данному занятию;

2) по номеру своего варианта выбрать условие задачи (см. лаб. раб. №1) и построить математическую модель двойственной задачи;

3) решить двойственную задачу линейного программирования с помощью надстройки Поиск решений в среде Excel (см. п.2);

4) после выполнения всех пунктов задания необходимо защитить отчет по работе.

Отчет по лабораторной работедолжен занимать 5-7 страниц и содержать:

• постановку экономической задачи (исходные данные варианта);

• экономико-математическую модель с необходимыми комментариями по ее элементам с указанием всех единиц измерения;

• протокол решения задачи, куда должны входить:

а) фрагмент исходного рабочего листа Excel;

б) диалоговое окно Поиск решения;

в) отчет по устойчивости и результаты его анализа c ответами на вопросы:

· Какие ресурсы в решенной задаче являются дефицитными?

· На сколько максимально можно увеличить запасы дефицитных ресурсов, сохранив при этом оптимальное решение?

· Как изменится целевая функция задачи, если один из дефицитных ресурсов максимально увеличить?

· Какие изделия являются эффективными в решаемой задаче? Показать с помощью теневых цен.

г) предложения (рекомендации) лицу, ответственному за принятие решений, по оптимальному управленческому поведению.

Отчет оформляется в установленные преподавателем сроки.

2. Инструкция по использованию
MICROSOFT EXCEL при решении двойственных задач линейного программирования

Рассмотрим в качестве примера решение средствами Microsoft Excel двойственной задачи к задаче о коврах:

В распоряжении фабрики имеется определенное количество ресурсов: рабочая сила (труд), сырье и оборудование. Фабрика может выпускать ковры четырех видов. Данные о запасах ресурсов, количестве единиц каждого ресурса, необходимых для производства одного ковра каждого вида, и доходах, получаемых предприятием от единицы каждого вида ковров, приведены в таблице:

Ресурсы	Запасы ресурсов	Нормы расходов ресурсов на единицу изделия
Ковер Тип 1	Ковер Тип 2	Ковер Тип 3	Ковер Тип 4
Труд, чел.- дн.
Сырье, кг
Оборудование, станко - час
Цена ед. изделия, тыс. руб.

Требуется найти такой план выпуска продукции, при котором стоимость выпущенной продукции будет максимальной.

Экономико-математическая модель двойственной задачи имеет вид:

где y₁ – теневая цена ресурса «труд»;

y₂ - теневая цена ресурса «сырье»;

y₃ - теневая цена ресурса «оборудование».

Решение двойственной задачи с помощью надстройки Excel Поиск решения

Решение двойственной задачи можно найти в Отчете по устойчивости решения исходной задачи (рис. 2.1).

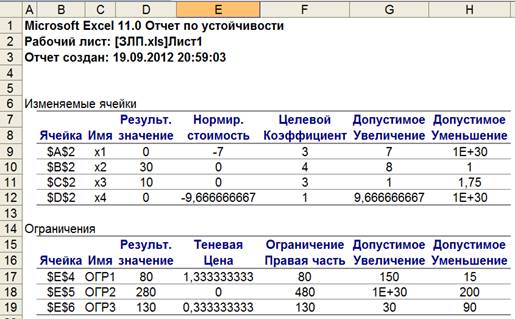
Рис. 2.1. Содержание отчета по устойчивости

Отчет по устойчивости содержит информацию, относящуюся к переменным:

• Результат решения задачи.

• «Нормированная стоимость» показывает, на сколько изменится значение целевой функции в случае принудительного включения единицы этой продукции в оптимальное решение. Например, в отчете по устойчивости для рассматриваемой задачи (см. рис. 2.1) нормированная стоимость для ковров первого типа равна -7 тыс. руб./шт. Это означает, что если мы, несмотря на оптимальное решение (0; 30; 10; 0), попробуем включить в план выпуска один ковер первого типа, то новый план выпуска принесет нам доход 143 тыс. руб., что на 7 тыс. руб. меньше, чем прежнее оптимальное решение.

• Коэффициенты целевой функции.

Во второй части Отчета по устойчивости содержится информация, относящаяся к ограничениям:

• Величина использованных ресурсов в колонке Результирующее значение.

• Ценность дополнительной единицы ресурса (теневые цены) рассчитываются только для дефицитных ресурсов.

Решение с помощью таблиц Excel
Вначале построим на листе Excel решение системы неравенств.
Рассмотрим первое неравенство x₁+3x₂≤18.
Построим граничную прямую x₁+3x₂=18 по двум точкам. Прямую обозначим (L1)(или Ряд1). Координаты х₂ считаем по формулам:

Для построения выбираем точечную диаграмму

Выбираем данные для прямой

Изменяем название прямой:

Выбираем макет диаграммы. Изменяем название осей координат:

Прямая (L1) на графике:

Решение строгого неравенства x₁+3x₂≤18 можно найти с помощью единственной пробной точки, не принадлежащей прямой (L1). Например, с помощью точки (0; 0)Ï(L1).
При подстановке координат точки (0; 0), получаем неравенство
0 + 3×0 < 18 или 0 < 18 .
Неравенство является верным, следовательно решением неравенства (1) будет та полуплоскость, в которой пробная точка расположена (на рисунке ниже прямой L1).
Затем решаем неравенство (2) 2x₁+x₂≤16.
Построим граничную прямую 2x₁+x₂=16 по двум точкам. Прямую обозначим (L2).

Прямая (L2) на графике:

Решение строгого неравенства 2x₁+x₂≤16 можно найти с помощью единственной пробной точки, не принадлежащей прямой (L2). Например, с помощью точки (0; 0)Ï(L2).
При подстановке координат точки (0; 0), получаем неравенство
2×0 + 0 < 16 или 0 < 16 .
Неравенство является верным, следовательно решением неравенства (2) будет та полуплоскость, в которой пробная точка расположена (на рисунке ниже прямой L2).
Затем решаем неравенство (3) x₂≤5.
Построим граничную прямую x₂=5 по двум точкам. Прямую обозначим (L3).
На листе Excel добавляем данные

Прямая (L3) на графике:

Решение строгого неравенства 2x₂<5 можно найти с помощью единственной пробной точки, не принадлежащей прямой (L3). Например, с помощью точки (0; 0)Ï(L3).
При подстановке координат точки (0; 0), получаем неравенство
0 < 5 .
Неравенство является верным, следовательно решением неравенства (3) будет та полуплоскость, в которой пробная точка расположена (на рисунке ниже прямой L3).
Затем решаем неравенство (4) 3x₂≤21.
Построим граничную прямую 3x₂=21 по двум точкам. Прямую обозначим (L4).
На листе Excel добавляем данные

Прямая (L4) на графике:

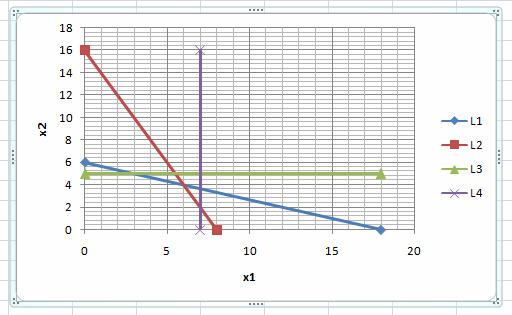
Решение строгого неравенства 3х₁ < 21 можно найти с помощью единственной пробной точки, не принадлежащей прямой (L4). Например, с помощью точки (0; 0)Ï(L4).
При подстановке координат точки (0; 0), получаем неравенство
0 < 21 .
Неравенство является верным, следовательно, решением неравенства (4) будет та полуплоскость, в которой пробная точка расположена (на рисунке левее прямой L4).
Решением двух неравенств (5) и (6) x₁≥0 и x₂≥0 является 1-ая четверть, ограниченная координатными прямыми x₁=0 и x₂=0.
Система неравенств решена. Решением системы неравенств (1) – (6) в данном примере является выпуклый многоугольник в левом нижнем углу рисунка, ограниченный прямыми L1, L2, L3, L4 и координатными прямыми x₁=0 и x₂=0. Убедиться, что многоугольник выбран правильно, можно подстановкой пробной точки, например (1; 1) в каждое неравенство исходной системы. При подстановке точки (1; 1) получаем, что все неравенства, в том числе естественные ограничения, верные.
Рассмотрим теперь целевую функцию
F = 2x₁ + 3x₂.
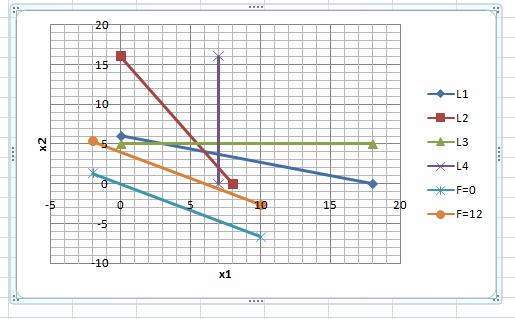
Построим линии уровня для значений функции F = 0 и F = 12 (числовые значения выбраны произвольно). На листе Excel добавляем данные

Линии уровней на графике:

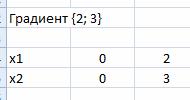
Построим вектор направлений (или градиент) . Координаты вектора совпадают с коэффициентами целевой функции F.
Добавляем на листе Excel координаты начальной и конечной точки вектора.

Вектор на рисунке:

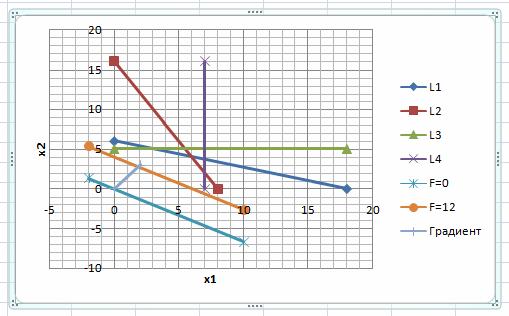
Градиент указывает направление увеличения целевой функции F.
Теперь следует линию уровня F=0 передвинуть параллельно до последней точки угловой точки выпуклого многоугольника. Последней угловой точкой пересечения выпуклого многоугольника и передвинутой линии уровня будет точка пересечения прямых L1 и L2. Для нахождения координат точки решим систему уравнений
x₁+3x₂=18
2x₁+x₂=16
Решаем систему уравнений по формулам Крамера. Для этого на листе Excel создаем массивы для определителей. Для вычисления определителей используем математическую функцию МОПРЕД

Выделяем массив определителя

Находим значения х₁ и х₂

Пересечением прямых L1 и L2 будет точка с координатами (6; 4).
Подставляем координаты точки в целевую функцию
Fmax= 2×6 +3×4 = 24
Ответ: Fmax= 24 при x₁=6 и x₂=4.

Алгоритм получения решения задачи симплекс-методом с использованием офисного приложения Microsoft Excel рассмотрим на примере 2.2.1. Математическая модель задачи имеет следующий вид:

Для получения решения исходной задачи будем использовать надстройку «Поиск решения».

Ввод исходных данных задачи

При решении задачи линейного программирования симплекс-методом с использованием офисного приложения Microsoft Excel необходимо сначала ввести данные задачи. Для этого создается новая рабочая книга Microsoft Excel, в свободные ячейки которой вносятся коэффициенты целевой функции, левой части ограничений, значения правой части ограничений.

Экранная форма для ввода условий задачи имеет следующий вид
(рис. 2.2.2):

В ячейках В4:С4 находятся значения коэффициентов целевой функции; в массиве В6:С8 –коэффициенты левой части ограничений; в столбце Е6:Е8значения правой части ограничений. Ячейки В2:С2соответствуют переменным задачи, а в ячейке Е2будет отображаться значение целевой функции. Сюда необходимо ввести формулу, по которой это значение рассчитывается, то есть . Для этого курсор ставится в ячейку и далее набирается следующее выражение: .

Имена ячеек можно набирать непосредственно с клавиатуры, либо делая на них ссылку мышью.

Значение целевой функции также можно рассчитать, используя надстройку «Мастер функций», а именно, функцию «СУММПРОИЗВ». Для этого необходимо выполнить следующие действия:

поставить курсор в поле Е2;

выбрать на панели инструментов кнопку ;

в окне «Категория» выбрать «Математические». В окне «Выберите функцию» «СУММПРОИЗВ» (рис. 2.2.3) и нажать «ОК»;

Ввести аргументы функции: в строку «Массив 1» выражение В2:С2, а в строку «Массив 2» выражение В4:С4 (можно, выделять соответствующие массивы с помощью мыши) (рис. 2.2.4) и нажать «ОК»;

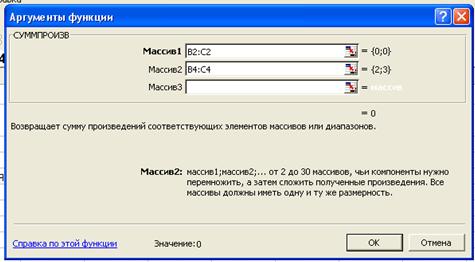
После этого в ячейке Е2 появится текущее значение целевой функции, вычисленное по введенной формуле. Оно равно нулю, так как переменные в данный момент равны нулю.

Аналогично в ячейки D6:D8вводятся формулы для расчета левых частей ограничений (рис. 2.2.5):

Для ячейкиD6формула имеет вид ,а ее реализация в ячейке: или =СУММПРОИЗВ(В2:C2; В6:C6).

Для ячейкиD7формула имеет вид ,а ее реализация в ячейке: или = СУММПРОИЗВ(В2:C2; В7:C7).

Для ячейкиD8формула имеет вид ,а ее реализация в ячейке: или = СУММПРОИЗВ(В2:C2; В8:C8).

Как видно, формулы для расчета левой части ограничений отличаются друг от друга только именем второго массива (строчки коэффициентов ограничения), первый же массив (массив значений переменных) один и тот же. Поэтому можно ввести формулу один раз, а затем скопировать ее, сделав абсолютную ссылку на массив переменных В2:C2.

Для того, чтобы сделать абсолютную ссылку на определенный столбец, необходимо поставить символ $, перед буквой, обозначающей имя столбца. Например $В2:$C2.Чтобы зафиксировать строку, символ $, ставится перед номером строки: В$2:C$2.Если необходимо сделать абсолютную ссылку на конкретную ячейку (ячейки), символ $ ставится и перед именем столбца и перед номером строки: $В$2:$C$2.

Абсолютную ссылку на ячейку (ячейки) можно сделать, нажав клавишу F4, когда курсор находится в поле имени ячейки. При однократном нажатии клавиши будет сделана абсолютная ссылка на массив или ячейку ($В$2: $C$2). Если клавишу нажать дважды, будет сделана абсолютная ссылка на номер строки (В$2: C$2). При следующем нажатии клавиши ссылка будет сделана на имя столбца ($В2: $C2).

При данном способе реализации симплекс-метода достаточно сделать ссылку лишь на соответствующую строку: В$2: C$2. В то же время допустима и абсолютная ссылка на конкретный массив ячеек: $В$2: $C$2.

Таким образом, для ячейки D6формула будет иметь вид или = СУММПРОИЗВ(В$2: C$2;В6:C6) (в случае абсолютной ссылки на массив = СУММПРОИЗВ($В$2: $C$2;В6:C6)).

Затем эту формулу необходимо скопировать в ячейки D7иD8.Копировать формулу можно с помощью клавиш «Ctrl-Insert» копировать и клавиш «Shift-Insert» вставить. Другой способ копирования формул поставить курсор в ячейку, содержащую формулу и протянуть ее за правый нижний угол на все ячейки, в которые ее необходимо скопировать.

После этого экранная форма условий задачи будет иметь вид (рис. 2.2.6).

Для получения решения задачи используется надстройка «Поиск решения», которая находится в меню «Сервис».

В диалоговом окне «Поиск решения» (рис. 2.2.7) необходимо выполнить следующие действия:

Поставить курсор в поле «Установить целевую ячейку» и ввести адрес ячейки, в которой находится формула для расчета значения целевой функции (можно сделать ссылку на ячейку мышью). В примере это ячейка E2.

Выбрать критерий оптимизации целевой функции (максимизация, минимизация или точное значение). В примере это максимум.

Поставить курсор в поле «Изменяя ячейки» и ввести адрес массива, в котором находятся значения переменных. В примере это В2:C2.Адрес можно внести также с помощью выделения мышью соответствующих ячеек.

В окне «Ограничения» выбрать кнопку «Добавить», после чего появится окно «Добавление ограничения» (рис. 2.6.8).

В поле «Ссылка на ячейку» ввести адрес ячейки, в которой содержится левая часть ограничения. (Это можно сделать путем выделения мышью соответствующей ячейки на экране). В поле знака открыть список предлагаемых знаков и выбрать нужный. В поле «Ограничения» ввести адрес ячейки, содержащей правую часть ограничений. В примере первое ограничение: D6<=E6в диалоговом окне представлено следующим образом (рис. 2.2.9)

Нажать кнопку «Добавить»и аналогично ввести остальные ограничения. Если при вводе ограничений задачи возникает необходимость изменить или удалить ограничения, то для этого используются кнопки «Изменить» и «Удалить» соответственно.

Диалоговое окно надстройки «Поиск решения» после ввода данных имеет следующий вид (рис. 2.2.10)

Для обеспечения выполнения условия неотрицательности переменных, а также установления конкретных параметров решения задачи оптимизации используется кнопка «Параметры» (рис. 2.2.11)

Установка флажка «Линейная модель» обеспечивает ускорение процесса решения линейной задачи, а установление флажка «Неотрицательные значения» неотрицательность переменных.

Подтверждаются установленные параметры нажатием кнопки «ОК».

В окне «Результат поиска решения» приведены типы отчета: «Результаты», «Устойчивость», «Пределы», которые используются для анализа чувствительности. Чтобы получить отчет, необходимо выбрать соответствующий тип и нажать кнопку «ОК». Результаты каждого отчета будут выведены на отдельных листах рабочей книги с названиями: «Отчет по результатам 1», «Отчет по устойчивости 1», «Отчет по пределам 1» (рис. 2.2.13)

Если необходимо получить только решение задачи, достаточно нажать кнопку «ОК» в диалоговом окне «Результат поиска решения» (рис. 2.2.12), после чего на экране в соответствующих ячейках появятся значения переменных и целевой функции. В нашем примере значения переменных находятся в ячейках В2:C2,а значение целевой функции – в ячейке E2(рис. 2.2.14).

Итак, решение задачи найдено: .

Заметим, что надстройка «Поиск решения» позволяет получать решение и в том случае, если в условии задачи все или некоторые переменные могут принимать только целые значения. Для получения целочисленного решения приведенной выше задачи в описанный процесс необходимо внести некоторые дополнения.

Дополнения вносятся на этапе ввода ограничений. К имеющимся в задаче ограничениям необходимо добавить условие целочисленности переменных. Для этого в диалоговом окне «Поиска решения» надо выбрать кнопку «Добавить», в поле «Ссылка на ячейку» ввести адрес ячеек, содержащих значения переменных (в примере это ячейки В2:С2),а в поле ввода знака ограничения выбрать целое(цел). (рис.2.2.15)

Подтверждается ввод условия целочисленности нажатием кнопки «ОК». Если задача имеет альтернативное решение, то с помощью компьютера получаем только одно решение.

Чтобы провести анализ чувствительности, необходимо в диалоговом окне «Результаты поиска решения» выделить с помощью мыши требуемый тип отчета: «Результаты», «Устойчивость», «Пределы» (рис. 2.2.16) и нажать кнопку «ОК».

Результаты каждого отчета будут выданы на отдельных листах рабочей книги (рис. 2.2.17; 2.2.18; 2.2.19).

В таблице «Отчет по результатам» приведена информация о значениях переменных, целевой функции, а также статусе ограничений (рис. 2.2.17).

Рис. 2.2.17. Отчёт по результатам (первая таблица)

В первой таблице указано оптимальное значение целевой функции. Результат: 52 000.

Вторая таблица позволяет найти значения переменных принятия решения (результат: ).

В третьей таблице отчета указаны значения левой части ограничений при данных значениях переменных, статус ограничений (связующее или не связующее), а также разность между правой и левой частью. Для связующих ограничений разность равна нулю, для не связующих – больше нуля

«Отчет по устойчивости» состоит из двух таблиц (рис. 2.2.18).

В первой таблице приведена информация о переменных.

1. Результат решения, то есть значения переменных.

2. Нормированная стоимость, или альтернативная цена, которая для небазисных переменных показывает, как изменится значение целевой функции, если соответствующую переменную ввести в базис со значением, равным единице. Для базисных переменных нормированная стоимость равна нулю. В данной задаче обе переменные являются базисными, поэтому их альтернативная цена равна нулю.

3. Коэффициенты целевой функции при соответствующих переменных.

4. Предельные приращения коэффициентов целевой функции, при которых текущее базисное решение не изменится. Так, для переменной границы устойчивости коэффициента целевой функции составляют , поскольку максимальное увеличение коэффициента возможно на 200, а уменьшение на 50. Другими словами, текущее оптимальное решение не изменится, пока цена за единицу первого вида продукции будет находиться в пределах от 250 до 500 грн.

Рис. 2.2.18. Отчёт по устойчивости (вторая таблица)

Вторая таблица содержит данные об ограничениях.

1. В столбце «Результ. значение» указано значение левой части ограничений.

2. В столбце «Теневая цена» находится решение двойственной задачи. Теневая цена показывает, на сколько изменится значение целевой функции, если правая часть ограничения увеличится на одну единицу. В приведенном примере третье ограничение не является связующим, то есть, третий вид сырья используется не полностью. Таким образом, можно закупать его меньше на соответствующую величину, то есть на 100 единиц. Это уменьшит затраты как на закупку сырья, так и на его хранение. Теневая цена первого ограничения, равная 400, свидетельствует о том, что каждая дополнительная единица третьего вида сырья увеличит прибыль на 400 грн. Можно также утверждать, что это максимальная цена, которую можно заплатить за 1 единицу сырья первого вида.

3. В столбцах «Допустимое увеличение (уменьшение)» находятся предельные приращения правых частей ограничений, при которых текущий опорный план не изменится. В примере для первого вида сырья границы устойчивости , так как допустимое уменьшение возможно на 25 ед., а увеличение на 20 Для второго вида сырья границы устойчивости составляют (100; 140), а для третьего – (200; ) (здесь 1Е+30 равносильна ). Это означает, что, до тех пор, пока количество сырья будет находиться в данных пределах, оптимальное решение задачи не изменится.

«Отчет по пределам»для рассматриваемой задачи имеет следующий вид (рис. 2.2.19):

Рис. 2.2.19. Отчёт по пределам (третья таблица)

Необходимо отметить, что для задач целочисленного программирования отчеты по устойчивости и пределам не применимы.

Необходимо отметить, что при решении задачи с использованием надстройки «Поиск решения» не важно, в какой форме записана задача линейного программирования и содержит ли система ограничений полный единичный базис. Решение осуществляется так, как было описано выше.

Для составления и анализа двойственной задачи рассмотрим вначале дополнительно основные понятия двойственности.

При составлении двойственных задач будем пользоваться определением. Если задача задана на max то ограничение вида «£» будем называть согласованным или правильным, а «³» – неправильным, несогласованным. Если задача задана на min, то ограничение « ³ » – правильное, а « £ » – неправильное.

Для написания двойственной задачи сформулируем соотношение между отдельными элементами прямой и двойственной задач:

1. Количество двойственных переменных равно количеству ограничений исходной задачи (каждому ограничению ставится в соответствие двойственная переменная).

2. Целевая функция двойственной задачи имеет вид F = b₁y₁+ b₂y₂+…+ b_my_m.

3. Если Z ® max, то F ® min; если Z ® min, то F ® max (направление цели F противоположно направлению цели Z).

4. Количество ограничений двойственной задачи равно количеству переменных исходной задачи. Каждой переменной исходной задачи ставится в соответствие ограничение двойственной задачи.

5. Левая часть j-го ограничения двойственной задачи равна , а правая с_j. Если , то j-е ограничение в двойственной задаче правильное. Если , то j-е ограничение – неправильное, если имеет любой знак, то j-е ограничение является равенством.

6. Если i-е ограничение исходной задачи правильное, то , если i-е ограничение исходной задачи неправильное, то , если i-е ограничение исходной задачи « = », то может иметь любой знак.

7. Матрицы исходной и двойственной задач взаимно транспонированные.

Для задачи оптимального выпуска продукции прямая и двойственная записываются в виде:

Прямая задача. Двойственная задача.

Рассмотрим составление двойственной задачи к исходной в общем случае на примере. Написать двойственную задачу к заданной задаче.

Прямая задача Двойственная задача

Решение двойственной задачи можно получить, исследуя решение исходной на основании первой и второй теорем двойственности.

Первая теорема двойственности.Если одна из пары двойственных задач имеет оптимальное решение, то вторая также имеет оптимальное решение, причем

Если одна из пары двойственных задач не ограничена, то у второй несовместна система ограничений.

Если одна из пары двойственных задач несовместна, то вторая несовместна или неограниченная.

Оптимальные значения переменных двойственной задачи можно определять из индексной строки последней симплексной таблицы по следующему правилу.

Чтобы найти надо:

1) в первой строке первой симплексной таблицы выбрать столбец, в котором находится базисная переменная. Пусть это будет столбец, соответствующий вектору ;

2) в этом столбце взять число, которое находится в индексной строке последней симплексной таблицы, т.е. ;

3) к этому числу прибавить коэффициент целевой функции из этого столбца. Это будет , т.е. .

Аналогично по второй, третьей строке и т. д. первой симплексной таблицы и элементам индексной строки последней таблицы находятся , и т. д.

При нахождении решения двойственной ЗЛП надо пользоваться правилом:

при умножении целевой функции на -1 двойственные переменные меняют знак.

при дописывании балансовых и искусственных переменных значения двойственных переменных не изменяются.

при умножении i-го ограничения на -1 i-я двойственная переменная меняет знак.

Значения двойственных переменных можно выписать из значения теневых цен.

4. Напишем двойственную задачу в примере 2.2.1.

5. Находим значения двойственных переменных из табл. 2.2.5.

Их можно выписать из теневых цен или из индексной строки последней симплекс-таблицы.

На рис. 22 - 25 и табл. 9 отражена последовательность действий, необходимая для получения решения задачи.

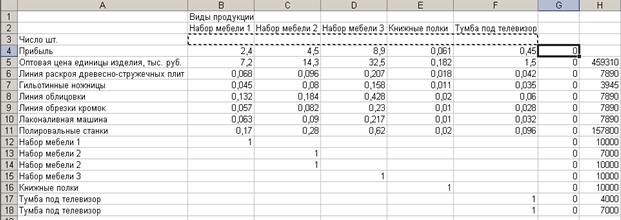
Рис. 22. Рабочий лист Excel с введенными данными

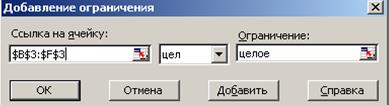
Рис. 23. Введение ограничений целочисленности переменных

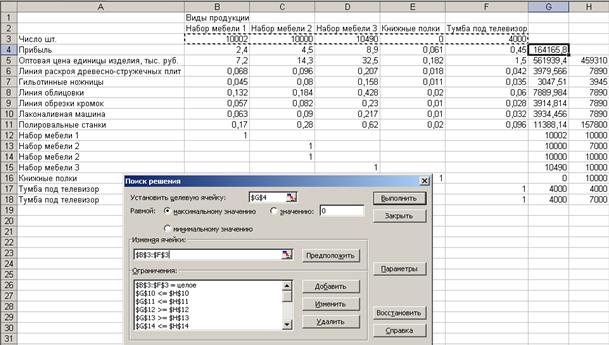
Рис. 24. Введены все условия для решения задачи

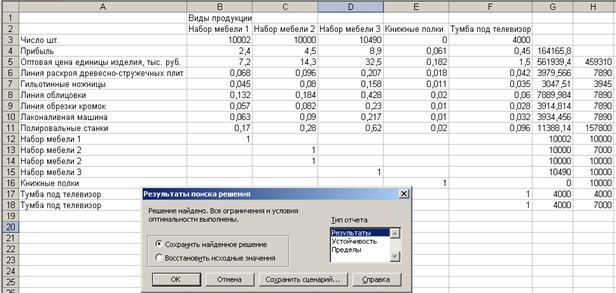
Рис. 25. Решение найдено. Все ограничения и условия оптимальности выполнены

Таблица 9 Результаты применения надстройки Поиск решений

Виды продукции
Набор мебели	Книжные полки	Тумба под телевизор
Количество, шт.	10 000
Прибыль	2,4	4,5	8,9	0,061	0,45
Ограничения (часть)	Левая	Правая
Оптовая цена единицы изделия, тыс. руб.	7,2	14,3	26,9	0,243	1,5
Линия раскроя древесностружечных плит	7889,98	0,068	0,096	0,207	0,018	0,042
Гильотинные ножницы	3047,51	0,045	0,080	0,158	0,011	0,035
Линия облицовки	7889,98	0,132	0,184	0,428	0,020	0,060
Линия обрезки кромок	3914,81	0,057	0,082	0,230	0,010	0,028
Лаконаливная машина	3934,46	0,063	0,090	0,217	0,010	0,032
Полировальные станки	11388,1	0,170	0,280	0,620	0,020	0,096
Набор мебели 1
Набор мебели 2
Набор мебели 2
Набор мебели 3
Книжные полки
Тумба под телевизор
Тумба под телевизор

Ответ. Для получения максимальной прибыли необходимо произвести:

Читайте также: