Задача о ранце решение в excel
Обновлено: 04.07.2024
Ниже приведен алгоритм точного решения целочисленной задачи о рюкзаке. Предлагаемый алгоритм требует меньше вычислительных ресурсов и возможно несколько проще алгоритма динамического программирования (ДП).
Первая версия описания алгоритма было послана мною в институт математики им. С. Л. Соболева Сибирского отделения РАН, откуда был прислан ответ что указанный алгоритм известен давно. Цитирую:
Одно из его первых упоминаний в книге Кереллера Nemhauser, Ullman, Discrete dynamic programming and capital allocation, Management Science, 15 p. 494-505, 1969.Тем не менее я решил ознакомить сообщество с алгоритмом, т.к. в известных мне учебниках по дискретной математике я его не обнаружил (возможно плохо искал). В первой версии алгоритма была ошибка, указанная мне пользователем wataru. За это ему большое спасибо. Я постарался эту ошибку устранить. До алгоритма я дошел самостоятельно, так что надеюсь ничьих прав не нарушаю. Возможно кому нибудь описание будет интересно и пригодится.
Введение
- полный перебор
- метод ветвей и границ
- динамического программирования (ДП)
Описание алгоритма решения задачи о рюкзаке с элементами псевдокода
START // начало алгоритма
Этап 1 // сортировка ИД
Сортируем ИД в порядке уменьшения удельной стоимости предметов:
P(1) / W(1) >= P(2) / W(2) >= . >= P(i) / W(i)>=… >= P( N) / W(N)
где P(i) > 0 стоимость предмета i , W(i) >0 вес предмета i.
В массиве X(1. N) все элементы первоначально = 0.
Для снижения потребности в памяти для алгоритма определяем минимальный вес в наборе ИД W_min = min( W )
Этап 2 // инициализация рабочих массивов
Создаем массив вещественных чисел LP размерностью (W_min… С)
и массив целых чисел LCr размерностью (W_min… С) . Заносим в массив LP и LCr данные первого элемента из отсортированного списка ИД
где P(1) стоимость и W(1) вес первого предмета в отсортированном списке ИД.
Этап 3 // заполнение рабочих массивов
Пусть W(i) и P(i) вес и стоимость текущего элемента ИД.
Создаем пустой массив вещественных чисел Clone размерностью (W_min… С).
Вносим в массив Clone стоимость текущего элемента ИД .
Копируем в массив Clone ненулевые данные из массива LP добавляя стоимость P(i) текущего элемента и увеличивая его индекс на его вес W(i), при условии что индекс в Clone не превзойдет вместимости рюкзака C.
Проводим модификацию массивов LP, LCr на основе данных массива Clone. Обновляем в массивах LP,LCr только те элементы стоимость которых в Clone больше чем в LP.
Этап 4 // формирование результата, обратный спуск
В массиве LP находим максимальное значение стоимости Pmax = MAX( LP ), это стоимость найденного оптимального решения. Индекс найденного в массиве элемента равен весу решения, обозначим его Wr, т.е. LP( Wr) = Pmax. Внесем первый найденный элемент в X:
далее
Выходим из цикла UNTIL и повторяем этапы 2, 3, 4 ( только на этапе 2 массивы LP, LCr не создаем, a заполняем нулями ). Повторять этап 1 (сортировка ИД) не нужно. Это по существу рекурсия, но из за предварительной сортировки ИД, она будет не глубокой. На некоторых наборах ИД рекурсии вообще может не быть. При повторе расчетов рассматриваем только те ИД, индекс которых меньше LCr( Wr ) и снижаем требуемый размер рюкзака до достигнутого веса Wr.
FINISH // конец алгоритма
Стоимость найденного решения Σ P(i) X(i), вес Σ W(i) X(i).
Правильность расчета итоговой стоимости рюкзака легко доказывается по индукции. Восстановление оптимального набора предметов, тоже не вызывает затруднений. Представленный алгоритм позволяет получить точное решение целочисленной задачи о рюкзаке.
В общем виде задача о рюкзаке формулируется следующим способом: имеется рюкзак определенного объема и неограниченное количество предметов. Для каждого предмета известен его объем (вес) и ценность (стоимость, эффективность). В рюкзак можно положить целое число предметов различного типа. Цель состоит в том, чтобы суммарная ценность всех находящихся в рюкзаке предметов была максимальна, а их объем (вес) не превышал заданной величины. К подобной формулировке может быть сведена задача максимального использования грузоподъемности подвижного состава, грузовместимости судна, автомобиля и т.п. Такая задача часто возникает при выборе оптимального управления в экономико-финансовых областях (например распределение бюджета отдела по проектам).
Решение задачи в классической постановке
Подобные задачи легко решаются с помощью надстройки "Поиск решения". Подготовлены исходные данные (рисунок ниже). Задача состоит в том, чтобы за счет подбора значений ячеек B16:B19 добиться максимального значения целевой функции (значение ячейки D20).
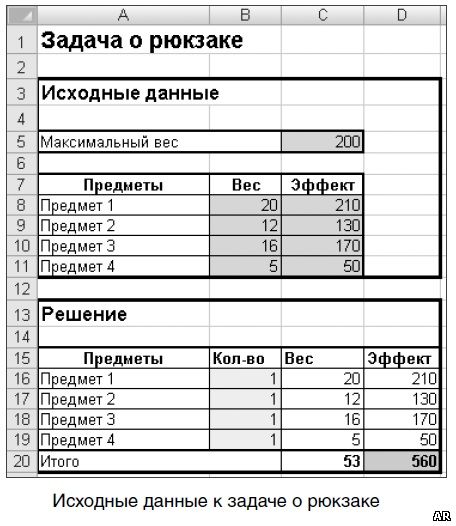
На первом рисунке ниже показаны ограничения на значения изменяемых ячеек. На втором рисунке ниже приводится результат расчета. Во многих практических случаях данная постановка задачи является слишком упрощенной. Далее будут рассмотрены варианты усложнения постановки задачи.
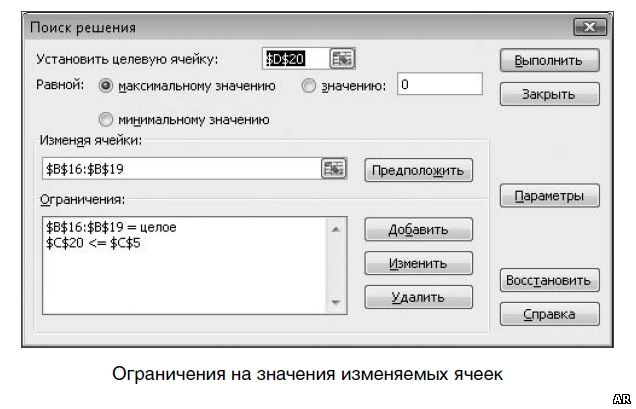

Модифицированная задача
Одним из дополнительных ограничений, возникающих при практическом использовании данной задачи, могут быть ограничения на необходимое количество предметов определенных видов, которые можно положить в рюкзак. При этом могут возникать варианты задачи, когда требуется строго определенное количество предметов или требуется не менее (не более) заданного количества предметов.
На рисунке ниже показаны исходные данные модифицированного варианта задачи. В этом случае предполагается, что в рюкзак может быть положено не менее некоторого количества предметов.
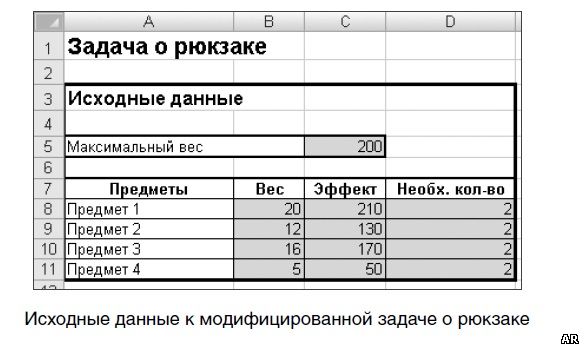
На следующем рисунке показаны ограничения на значения изменяемых ячеек B16:B19. В данном случае к ограничениям добавлено условие 16:19>=8:11, то есть задано минимальное необходимое количество предметов различных видов.

Решение задачи представлено последнем рисунке.

При необходимости дополнительное условие 16:19>=8:11 может быть изменено. Например, можно установить отдельные ограничения для всех предметов, назначив для некоторых из них точное количество предметов, в то время как для других — условие «не менее» или «не более»
Рассмотрим задачу коммивояжера (англ. Travelling Salesman Problem, TSP) заключающуюся в отыскании самого короткого маршрута, проходящего через заданные города по одному разу с последующим возвратом в исходный город (также рассмотрим вариант без возврата).
Задача
Найдем кратчайший путь между 5 городами, координаты которых известны. Рассмотрим замкнутый вариант задачи: коммивояжёру требуется посетить все города, после чего вернуться в исходный город.
Решение
Так как даны координаты городов, то сначала найдем расстояния между ними (см. файл примера, лист 5 городов ).


Расстояния рассчитаем с помощью формулы: = КОРЕНЬ((ИНДЕКС($C$7:$D$11;$F7+1;1)-ИНДЕКС($C$7:$D$11;G$6+1;1))^2 +(ИНДЕКС($C$7:$D$11;$F7+1;2)-ИНДЕКС($C$7:$D$11;G$6+1;2))^2)

Теперь создадим модель для Поиска решения .

Совет : Вводная статья про Поиск решения в MS EXCEL 2010 находится здесь .
Переменные (выделено зеленым) . В качестве переменных модели следует взять номера городов. Так как начальная и конечная точка известны (Город0), то переменных будет 4. Ограничения (выделено синим) . Необходимо, чтобы номера городов не повторялись. Это означает, что количество уникальных (неповторяющихся) номеров городов должно быть равно 4. Для этого используется формула для подсчета уникальных значений : = СУММПРОИЗВ(1/СЧЁТЕСЛИ(B16:B19;B16:B19))
Целевая функция (выделено красным) . Длина маршрута должна быть минимальной.

Примечание : для удобства настройки Поиска решения используются именованные диапазоны .
Выберите Эволюционный метод поиска решения, т.к. созданная модель не является линейной из-за наложенного на переменные ограничения.
Найденное Решение
Поиск решения найдет (должен найти) самый короткий маршрут, т.е. последовательность 0-1-4-2-3-0 (или обратную).

В этой простейшей задаче можно проверить, действительно ли этот маршрут имеет минимальную длину, путем перебора всех вариантов маршрутов. Это реализовано в файле примера .
Совет . Таблицы перебора перестановок от 1 до 5, от 1 до 6, … от 1 до 9 можно найти в этой статье Перебор всех возможных Перестановок в MS EXCEL .
Результаты Эволюционного метода сильно зависят от начальных условий и параметров его настройки (скорость изменения, размер совокупности). Повторный поиск, с теми же начальными условиями и параметрами, может привести к различным результатам. Убедиться в этом можно с помощью модели, созданной в файле примера на листе 11 городов.

Обнулите значения переменных модели на Листе 11 городов, запустите Поиск решения. После окончания поиска (может занять несколько минут) опять обнулите значения переменных и перезапустите Поиск решения: найденные решения могут серьезно отличаться.
Совет . Иногда, для того чтобы улучшить найденное решение, помогает следующий прием: запустите Поиск решения , сохраните найденное решение, измените параметры поиска (например, размер совокупности), повторно запустите Поиск решения.
В файле примера также приведено решение задачи для замкнутого и незамкнутого маршрута посещения 9 городов. Решения найдены с помощью Эволюционного метода со следующими параметрами: Целочисленная оптимальность 0%, Использовать автоматическое масштабирование, Скорость изменения варьировалась 0,25-0,5; Размер совокупности варьировался 10-50. Оба решения проверены с помощью таблиц перебора всех маршрутов (см. таблицы перебора перестановок ). Если при первом прогоне Поиска решения не удавалось найти оптимальное решение, то он запускался повторно, при этом 1 или 2 параметра изменялись. После второго прогона оптимальное решение, как правило, было найдено.


Вывод : задачу коммивояжера (граф полностью связный, гамильтоновый цикл) можно решить стандартным Поиском решения с помощью построения нелинейных моделей. При количестве вершин графа (городов)
В этой статье мы отойдем от формулировки практических задач и решим задачу линейного программирования в абстрактных терминах: вектор переменных х, матрица ограничений A х , вектор b , целевая функция cTx (вместо более привычных: объем производства, количество комплектующих разного вида, максимальный доход). Задача линейного программирования (ЛП) есть задача максимизации линейной функции при линейных ограничениях. Задачу ЛП можно записать несколькими стандартными способами. Мы сформулируем ее в форме max cTx : Ax 0>
Задача
Необходимо максимизировать целевую функцию cTx: max 50* x1 + 30* x2 + 25* x3 + 30* x4 при условии, что: 2* x1 + 2,5* x2 + 3* x3 + 1,8* x4 = 50 x3 >= 30 x1; x2; x3; x4 >= 0
cTx - это векторное произведение векторов cT (транспонированный вектор с) и х.
Примечание : эта задача эквивалентна задаче определения оптимальной структуры производства с целью максимизации дохода (см. статью Поиск решения MS EXCEL (1.1). Оптимальная структура выпускаемой продукции ). Сформулируем эту задачу в общем виде: Предприятие планирует производить n видов продукции, используя m видов ресурсов. Для производства единицы j-го продукта требуется aij единиц i-го ресурса. Стоимость единицы j-го продукта равна cj. В наличии имеется bi единиц i-го ресурса. Нужно определить план производства с целью максимизировать прибыль. Обозначив хj - объем выпуска продукции j-го вида (j =1;…;n), мы можем записать задачу поиска оптимального производственного плана следующим образом:

Или в матричной форме:

Получается, что в исходной задаче:
- вектор с (стоимость продукции) равен (50; 30; 25; 30)
- вектор x (количество продукции) необходимо найти для заданных условий
- n=4 (4 вида продукции)
- m=3 (3 вида ресурсов)
- вектор b (количество ресурсов) равен (800; 400; 380)
- матрица A (количество единиц ресурсов для изготовления продукта) равна (2; 2,5; 3; 1,8 : 1,2; 1; 2; 0,8 : 1,5; 1,2; 1,5; 0,8)
Теперь создадим модель.
Создание модели
На рисунке ниже приведена модель, созданная для решения задачи (см. файл примера ).
Для решения задачи на листе MS EXCEL необходимо записать матрицу А , вектора b и cT (предварительно все неравенства переведены в форму меньше или равно путем умножения соответствующих уравнений на -1):


Примечание : для удобства настройки Поиска решения используются именованные диапазоны .
Совет : Вводная статья про Поиск решения в MS EXCEL 2010 находится здесь .
Значение целевой функции cTx получено путем матричного умножения векторов cT и x (используйте функцию МУМНОЖ() , которая вводится как формула массива ). Аналогично получена функция ограничений Ах , путем умножения матрицы А на х . Так как матрица Ах имеет размерность 5х1, то перед вводом формулы = МУМНОЖ(Матрица_А;Вектор_Х) необходимо выделить столбец из 5 ячеек, затем после записи формулы в Строке формул , нажмите CTRL + SHIFT + ENTER для ее ввода.
Условие 0-1 knapsack problem:
Из множества предметов со свойствами «стоимость» и «вес», отобрать некоторое их число таким образом, чтобы получить максимальную суммарную стоимость при одновременном соблюдении ограничения на суммарный вес.
Динамическое программирование. Что меня поразило в этом алгоритме
Ведь задан вес - Р.
Кажется, кратчайшее решение - это рассматривать наборы только этого веса.
Число сочетаний С из n по m возрастает с увеличением m [от 1 до n/2], а затем будет убывать.
Так зачем рассматривать промежуточные наборы и тратить время.
Отсортировать предметы по убыванию «стоимости» и перебирать в цикле, проверяя условие: вес ячейки одной строки) и увеличивая количество предметов от 1 до n (внешний цикл > увеличение номера строки) становится возможной автоматическая оптимизация.
Делая выбор для очередной ячейки, выбирается максимум из двух вариантов:
Первый вариант: ячейка в этой же колонке, но на строку выше (т.е. просто, не брать этот предмет в ранец, т.к. предыдущий набор предметов для данного веса «ценнее»).
Второй вариант: стоимость предмета + ячейка, которая на строку выше и левее на величину веса предмета (т.е. берем предмет, но выбрасываем из ранца другие предметы на величину его веса).
А как красиво заполняется таблица Иногда, оказывается, следует выбрасывать предметы с большей удельной стоимостью, чтобы достичь максимальной загрузки ранца и от этого получить максимум стоимости в результат.
И даже сортировка излишня. Без нее результат абсолютно тот же. Предмет с большим удельным весом всегда будет размещаться алгоритмом (в строке таблицы) левее, чем остальные.
Экспериментируйте. Все наглядно.
В желтых ячейках можно задать параметры.
Кнопки Random, Sort, Massiv запускают определенные макросы.
Пример решений задачи на VBA Excel 2007 и выше
А это Задача о ранце (рюкзаке) на VBA Excel 2010.
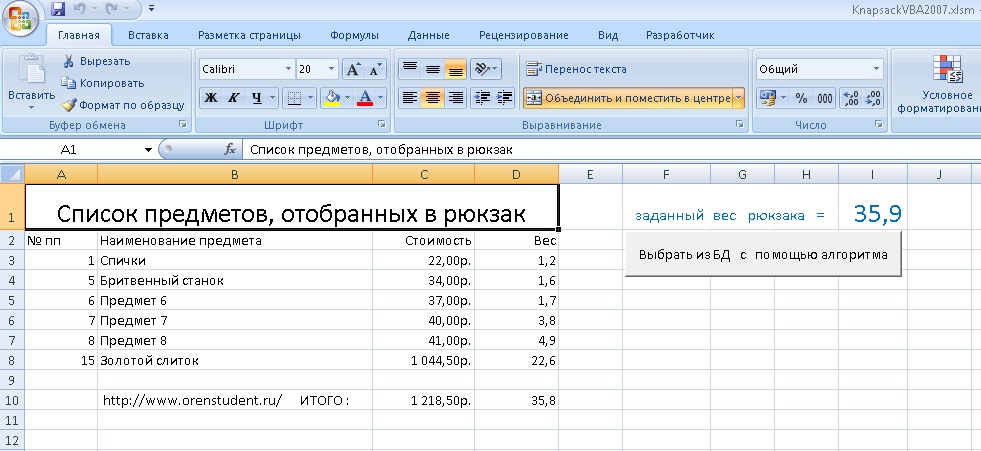
Рис.1 Пример решений задачи на VBA Excel
Читайте также:

