Как посчитать соотношение сторон треугольника

Обновлено: 07.07.2024

Треугольник – это многоугольник с тремя сторонами (или тремя углами). Стороны треугольника обозначаются часто малыми буквами, которые соответствуют заглавным буквам, обозначающим противоположные вершины.

Если все три угла острые ( рис.20 ), то это остроугольный треугольник . Если один из углов прямой ( C, рис.21 ), то это прямоугольный треугольник; стороны a , b , образующие прямой угол, называются катетами; сторона c , противоположная прямому углу, называется гипотенузой. Если один из углов тупой ( B, рис.22 ), то это тупоугольный треугольник.

Треугольник ABC ( рис.23 ) - равнобедренный , если две его стороны равны ( a = c ); эти равные стороны называются боковыми, третья сторона называется основанием треугольника. Треугольник ABC ( рис.24 ) – равносторонний , если все его стороны равны ( a = b = c ). В общем случае ( a ≠ b ≠ c ) имеем неравносторонний треугольник.

Основные свойства треугольников. В любом треугольнике:

1. Против большей стороны лежит больший угол, и наоборот.

2. Против равных сторон лежат равные углы, и наоборот.

В частности, все углы в равностороннем треугольнике равны.

3. Сумма углов треугольника равна 180 º .

Из двух последних свойств следует, что каждый угол в равностороннем

треугольнике равен 60 º.

4. Продолжая одну из сторон треугольника ( AC , рис.25), получаем внешний

угол BCD . Внешний угол треугольника равен сумме внутренних углов,

не смежных с ним : BCD = A + B .

5. Любая сторона треугольника меньше суммы двух других сторон и больше

их разности ( a < b + c, a > b – c; b < a + c, b > a – c; c < a + b, c > a – b ).

Признаки равенства треугольников.

Треугольники равны, если у них соответственно равны:

a ) две стороны и угол между ними;

b ) два угла и прилегающая к ним сторона;

c ) три стороны.

Признаки равенства прямоугольных треугольников.

Д ва прямоугольных треугольника равны, если выполняется одно из следующих условий:

1) равны их катеты;

2) катет и гипотенуза одного треугольника равны катету и гипотенузе другого;

3) гипотенуза и острый угол одного треугольника равны гипотенузе и острому углу другого;

4) катет и прилежащий острый угол одного треугольника равны катету и прилежащему острому углу другого;

5) катет и противолежащий острый угол одного треугольника равны катету и противолежащему острому углу другого.

Замечательные линии и точки в треугольнике.

Высота треугольника - это перпендикуляр, опущенный из любой вершины на противоположную сторону ( или её продолжение ). Эта сторона называется основанием треугольника . Три высоты треугольника всегда пересекаются в одной точке , называемой ортоцентром треугольника. Ортоцентр остроугольного треугольника ( точка O , рис.26 ) расположен внутри треугольника, а ортоцентр тупоугольного треугольника ( точка O , рис.27 ) – снаружи; ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла.

Медиана – это отрезок , соединяющий любую вершину треугольника с серединой противоположной стороны. Три медианы треугольника ( AD , BE , CF , рис.28 ) пересекаются в одной точке O , всегда лежащей внутри треугольника и являющейся его центром тяжести. Эта точка делит каждую медиану в отношении 2:1, считая от вершины.

Биссектриса – это отрезок биссектрисы угла от вершины до точки пересечения с противоположной стороной. Три биссектрисы треугольника ( AD , BE , CF , рис.29 ) пересекаются в одной точке О, всегда лежащей внутри треугольника и являющейся центром вписанного круга (см. раздел «Вписанные и описанные многоугольники»).

Биссектриса делит противоположную сторону на части, пропорциональные прилегающим сторонам ; например, на рис.29 AE : CE = AB : BC .

Срединный перпендикуляр – это перпендикуляр, проведенный из средней точки отрезка (стороны). Три срединных перпендикуляра треугольника АВС ( KO , MO , NO , рис.30 ) пересекаются в одной точке О, являющейся центром описанного круга ( точки K , M , N – середины сторон треугольника ABC ).

В остроугольном треугольнике эта точка лежит внутри треугольника; в тупоугольном – снаружи; в прямоугольном - в середине гипотенузы. Ортоцентр, центр тяжести, центр описанного и центр вписанного круга совпадают только в равностороннем треугольнике.

Теорема Пифагора. В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Доказательство теоремы Пифагора с очевидностью следует из рис.31. Рассмотрим прямоугольный треугольник ABC с катетами a , b и гипотенузой c .

Построим квадрат AKMB , используя гипотенузу AB как сторону. Затем продолжим стороны прямоугольного треугольника ABC так, чтобы получить квадрат CDEF , сторона которого равна a + b . Теперь ясно, что площадь квадрата CDEF равна ( a + b ) 2 . С другой стороны, эта площадь равна сумме площадей четырёх прямоугольных треугольников и квадрата AKMB , то есть

Типы треугольников

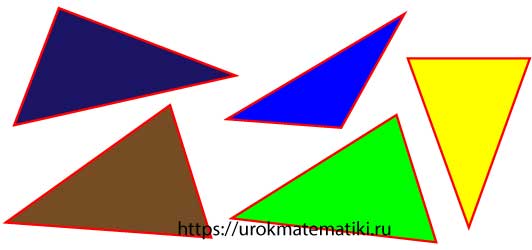
По величине углов

Остроугольный треугольник

Тупоугольный треугольник

Прямоугольный треугольник

По числу равных сторон

Разносторонний треугольник

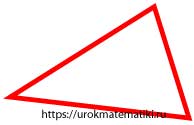
Равнобедренный треугольник

Равносторонний (правильный) треугольник

Вершины, углы и стороны треугольника

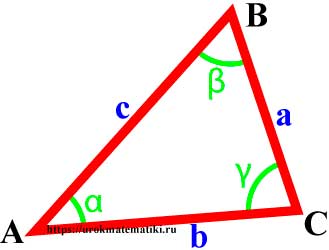
Свойства углов и сторон треугольника

Сумма углов треугольника равна 180°

В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы

если α > β , тогда a > b
если α = β , тогда a = b

Сумма длин двух любых сторон треугольника больше длины оставшейся стороны

Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов.

a sin α = b sin β = c sin γ

Теорема косинусов

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведение этих сторон на косинус угла между ними.

a 2 = b 2 + c 2 - 2 b c · cos α
b 2 = a 2 + c 2 - 2 a c · cos β
c 2 = a 2 + b 2 - 2 a b · cos γ

Теорема о проекциях

Для остроугольного треугольника:

a = b cos γ + c cos β
b = a cos γ + c cos α;
c = a cos β + b cos α;

Формулы для вычисления длин сторон треугольника

Формулы сторон через медианы

a = 2 3 2 m b 2 + m c 2 - m a 2

b = 2 3 2 m a 2 + m c 2 - m b 2

c = 2 3 2 m a 2 + m b 2 - m c 2

Медианы треугольника

Свойства медиан треугольника

Медианы треугольника пересекаются в одной точке. Точка пересечения медиан называется центроидом.

S ∆AOF = S ∆AOE = S ∆BOF = S ∆BOD = S ∆COD = S ∆COE

Формулы медиан треугольника

Формулы медиан треугольника через стороны

m a = 1 2 2 b 2 + 2 c 2 - a 2

m b = 1 2 2 a 2 + 2 c 2 - b 2

m c = 1 2 2 a 2 + 2 b 2 - c 2

Биссектрисы треугольника

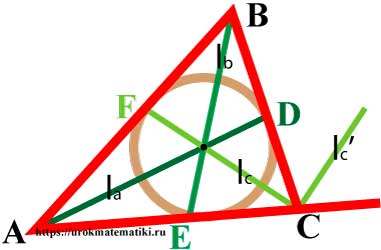
Свойства биссектрис треугольника

Биссектрисы треугольника пересекаются в одной точке, равноудаленной от трех сторон треугольника, - центре вписанной окружности.

Угол между l c и l c ' = 90°

Формулы биссектрис треугольника

Формулы биссектрис треугольника через стороны

l a = 2 b c p p - a b + c

l b = 2 a c p p - b a + c

l c = 2 a b p p - c a + b

Формулы биссектрис треугольника через две стороны и угол

l a = 2 b c cos α 2 b + c

l b = 2 a c cos β 2 a + c

l c = 2 a b cos γ 2 a + b

Высоты треугольника

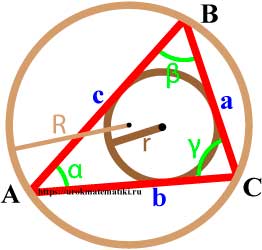
В зависимости от типа треугольника высота может содержаться:

Свойства высот треугольника

Высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника.

Формулы высот треугольника

Формулы высот треугольника через сторону и угол

h a = b sin γ = c sin β

h b = c sin α = a sin γ

h c = a sin β = b sin α

Формулы высот треугольника через сторону и площадь

Формулы высот треугольника через две стороны и радиус описанной окружности

Окружность вписанная в треугольник

Окружность называется вписанной в треугольник, если она касается всех трех его сторон.

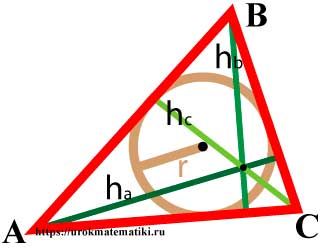
Свойства окружности вписанной в треугольник

Центр вписанной в треугольник окружности лежит на пересечении биссектрис внутренних углов треугольника.
В любой треугольник можно вписать окружность, и только одну.

Формулы радиуса окружности вписанной в треугольник

Радиус вписанной в треугольник окружности равен отношению площади треугольника к его полупериметру

Радиус вписанной в треугольник окружности через три стороны

Формулы высот треугольника через две стороны и радиус описанной окружности

Окружность описанная вокруг треугольника

Окружность называется описанной вокруг треугольника, если она содержит все вершины треугльника.

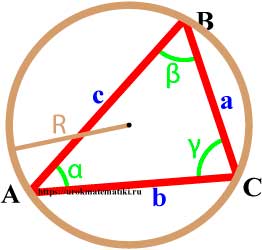
Свойства окружности описанной вокруг треугольника

Центр описанной вокруг треугольника окружности лежит на пересечении серединных перпендикуляров к его сторонам.
Вокруг любого треугольника можно описать окружность, и только одну.

Свойства углов

Центр описанной окружности лежит внутри остроугольного треугольника, снаружи тупоугольнго треугольника, на середине гипотенузы прямоугольного треугольника.

Формулы радиуса окружности описанной вокруг треугольника

Радиус описанной окружности через три стороны и площадь

Радиус описанной окружности через площадь и три угла

Радиус описанной окружности через сторону и противоположный угол (теорема синусов)

Связь между вписанной и описанной окружностями треугольника

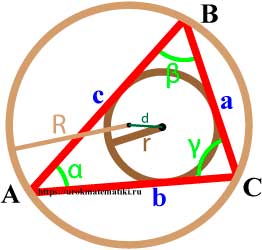
Формулы радиуса окружности описанной вокруг треугольника

d 2 = R 2 - 2 R r

Радиус описанной окружности через площадь и три угла

Средняя линия треугольника

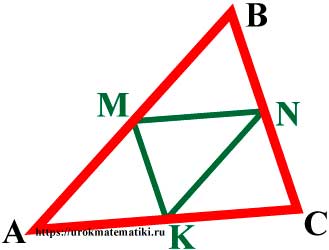
Свойства средней линии треугольника

Любой треугольник имеет три средних линии.
Средняя линия треугольника параллельна основанию и равна его половине.
MN = 1 2 AC ; KN = 1 2 AB ; KM = 1 2 BC

Признаки

Периметр треугольника

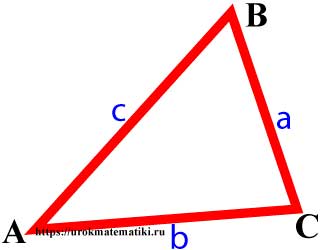
Периметр треугольника ∆ABC равен сумме длин его сторон.

Формулы площади треугольника

Формула площади треугольника по стороне и высоте

Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты.

S = 1 2 a · h a ,
S = 1 2 b · h b ,
S = 1 2 c · h c ,

Формула площади треугольника по трем сторонам

Формула Герона формула для вычисления площади треугольника S по длинам его сторон a, b, c .

S = p p - a p - b p - c ,

Формула площади треугольника по двум сторонам и углу между ними

Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.

S = 1 2 a · b · sin γ ,
S = 1 2 b · c · sin α ,
S = 1 2 a · c · sin β ,

Формула площади треугольника по трем сторонам и радиусу описанной окружности

Формула площади треугольника по трем сторонам и радиусу вписанной окружности

Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

Равенство треугольников

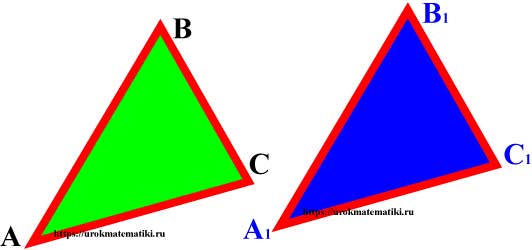
Определение

Если два треугольника АВС и А₁В₁С₁ можно совместить наложением, то они равны.

Свойства

У равных треугольников равны и их соответствующие элементы. (В равных треугольниках против равных сторон лежат равные углы, против равных углов лежат равные стороны).

Признаки равенства треугольников

По двум сторонам и углу между ними

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

По стороне и двум прилежащим углам

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

По трем сторонам

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Подобие треугольников

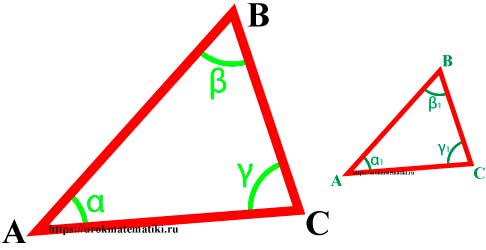
Определение

∆MNK => α = α 1 , β = β 1 , γ = γ 1 и AB MN = BC NK = AC MK = k

Признаки подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
Если две стороны одного треугольника пропорциональны двум сторонам другого, а углы, между этими сторонами, равны, то такие треугольники подобны.

Свойства

Площади подобных треугольников относятся как квадрат коэффициента подобия:

S ∆АВС S ∆MNK = k 2

Прямоугольные треугольники

Свойства прямоугольного треугольника

Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы (гипотенуза в два раза длиннее катета, лежащего против угла в 30°).

Докажем, что BC=2AC.
Приложим к треугольнику ABC равный ему треугольник ABD , как показано на рисунке.
Получим треугольник BCD, в котором ∡B = ∡D = 60° , поэтому DC = BC. Но DC = 2AC. Следовательно, BC = 2AC.

Справедливо и обратное суждение: Если катет прямоугольного треугольника равен половине гипотенузы (или гипотенуза в два раза длиннее катета), то угол, лежащий против этого катета, равен 30°.

Признаки равенства прямоугольных треугольников

Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.

Свойства

Площади подобных треугольников относятся как квадрат коэффициента подобия:

С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.

Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:

Три стороны треугольника.
Две стороны треугольника и угол между ними.
Две стороны и угол противостоящий к одному из этих сторон треугольника.
Одна сторона и любые два угла.

Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.

Решение треугольника по трем сторонам

Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем .

Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения

Пример 1. Известны стороны треугольника ABC: Найти (Рис.1).

Решение. Из формул (1) и (2) находим:

Используя онлайн калькулятор для arcsin и arccos находим углы A и B:

И, наконец, находим угол C:

Решение треугольника по двум сторонам и углу между ними

Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.

Найдем сторону c используя теорему косинусов:

Далее, из формулы

найдем cosA:

Далее из (3) с помощью калькулятора находим угол A.

Поскольку уже нам известны два угла то находим третий:

Пример 2. Известны две стороны треугольника ABC: и (Рис.2). Найти сторону c и углы A и B.

Решение. Иcпользуя теорму косинусов найдем сторону c:

Из формулы (3) найдем cosA:

Поскольку уже нам известны два угла то находим третий:

Решение треугольника по стороне и любым двум углам

Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.

Так как, уже известны два угла, то можно найти третий:

Далее, для находждения сторон b и c воспользуемся тероемой синусов:

Пример 3. Известна одна сторона треугольника ABC: и углы (Рис.3). Найти стороны b и c и угол С.

Решение. Поскольку известны два угла, то легко можно найти третий угол С:

228. В этой главе мы будем главным образом понимать под обозначениями отрезков AB, AC и т. д. выражающие их числа.

Мы знаем (п. 226), что если даны геометрически два отрезка a и b, то мы можем построить средний пропорциональный между ними. Пусть теперь отрезки даны не геометрически, а числами, т. е. под a и b будем понимать числа, выражающие 2 данных отрезка. Тогда нахождение среднего пропорционального отрезка сведется к нахождению числа x из пропорции a/x = x/b, где a, b и x числа. Из этой пропорции имеем:

229. Пусть имеем прямоугольный треугольник ABC (чер. 224).

Опустим из вершины его прямого угла (∠B прямой) перпендикуляр BD на гипотенузу AC. Тогда из п. 225 мы знаем:

1) AC/AB = AB/AD и 2) AC/BC = BC/DC.

Отсюда мы получаем:

AB 2 = AC · AD и BC 2 = AC · DC.

Сложив по частям полученные равенства, получим:

AB 2 + BC 2 = AC · AD + AC · DC = AC(AD + DC).

т. е. квадрат числа, выражающего гипотенузу, равен сумме квадратов чисел, выражающих катеты прямоугольного треугольника .

Сокращенно говорят: Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов .

Если мы дадим полученной формуле геометрическое толкование, то получим уже известную нам теорему Пифагора (п. 161):

квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на катетах.

Из уравнения AB 2 + BC 2 = AC 2 иногда приходится находить катет прямоугольного треугольника, по гипотенузе и другому катету. Получим, напр.:

AB 2 = AC 2 – BC 2 и, следов.,

230. Найденное числовое соотношение между сторонами прямоугольного треугольника позволяет решать множество вычислительных задач. Решим некоторые из них:

1. Вычислить площадь равностороннего треугольника по данной его стороне .

Пусть ∆ABC (чер. 225) равносторонний и каждая его сторона выражается числом a (AB = BC = AC = a). Для вычисления площади этого треугольника надо узнать сначала его высоту BD, которую мы назовем чрез h. Мы знаем, что в равностороннем треугольнике высота BD делит основание AC пополам, т. е. AD = DC = a/2. Поэтому из прямоугольного треугольника DBC имеем:

BD 2 = BC 2 – DC 2 ,

h 2 = a 2 – a 2 /4 = 3a 2 /4 (выполняем вычитание).

(выносим множитель из под корня).

Следовательно, называя число, выражающее площадь нашего треугольника, чрез Q и зная, что площадь ∆ABC = (AC · BD)/2, находим:

Мы можем смотреть на эту формулу, как на один из способов измерения площади равностороннего треугольника: надо измерить его сторону в линейных единицах, возвести найденное число в квадрат, умножить полученное число на √3 и разделить на 4 — получим выражение площади в квадратных (соответствующих) единицах.
2. Стороны треугольника равны 10, 17 и 21 лин. един. Вычислить его площадь .

Опустим высоту h в нашем треугольнике (чер. 226) на большую сторону — она непременно пройдет внутри треугольника, так как в треугольнике тупой угол может быть расположен только против большей стороны. Тогда большая сторона, = 21, разделится на 2 отрезка, один из которых обозначим чрез x (см. чертеж) — тогда другой = 21 – x. Получим два прямоугольных треугольника, из которых имеем:

h 2 = 10 2 – x 2 и h 2 = 17 2 – (21 – x) 2

Так как левые части этих уравнений одинаковы, то

10 2 – x 2 = 17 2 – (21 – x) 2

Выполняя действия получим:

10 2 – x 2 = 289 – 441 + 42x – x 2

Упрощая это уравнение, найдем:

Тогда из уравнения h 2 = 10 2 – x 2 , получим:

h 2 = 10 2 – 6 2 = 64

Тогда искомая площадь найдется:

Q = (21 · 8)/2 квад. един. = 84 квад. един.

3. Можно решить общую задачу:

как вычислить площадь треугольника по его сторонам?

Пусть стороны треугольника ABC выражены числами BC = a, AC = b и AB = c (чер. 227). Положим, что AC есть большая сторона; тогда высота BD пойдет внутри ∆ABC. Назовем: BD = h, DC = x и тогда AD = b – x.

Из ∆BDC имеем: h 2 = a 2 – x 2 .

Из ∆ABD имеем: h 2 = c 2 – (b – x) 2 ,

откуда a 2 – x 2 = c 2 – (b – x) 2 .

Решая это уравнение, последовательно получаем:

2bx = a 2 + b 2 – c 2 и x = (a 2 + b 2 – c 2 )/2b.

Далее, подставляя это выражение в уравнение h 2 = a 2 – x 2 , найдем

(Последнее написано на том основании, что числителя 4a 2 b 2 – (a 2 + b 2 – c 2 ) 2 можно рассматривать, как равность квадратов, которую разлагаем на произведение суммы на разность).

Эту формулу преобразовывают, вводя периметр треугольника, который обозначим чрез 2p, т. е.

Вычитая по 2c из обеих частей равенства, получим:

a + b + c – 2c = 2p – 2c или a + b – c = 2(p – c):

c + a – b = 2(p – b) и c – a + b = 2(p – a).

(p выражает полупериметр треугольника).
Этою формулою можно пользоваться для вычисления площади треугольника по трем его сторонам.

231. Упражнения.

Основание равнобедренного треугольника равно 10 дм., а его площадь = 60 кв. дм. Найти (вычислить) его периметр.
Параллельные стороны равнобочной трапеции равны 16 и 40 дм., а каждая из непараллельных сторон = 37 дм. Вычислить его площадь.
Стороны трапеции равны: параллельные 15 и 36 дм., а непараллельные 13 и 20 дм. Вычислить их площадь.
Сторона ромба и его меньшая диагональ одинаковы. Найти формулу для измерения площади такого ромба по его стороне.
Катеты прямоугольного треугольника равны соответственно 6 и 8 дм. Найти отрезок гипотенузы, заключенный между биссектором прямого угла треугольника и высотою, опущенною из вершины прямого угла.
Биссектор прямого угла прямоугольного треугольника делит гипотенузу на 2 отрезка, равные соответственно лин. един. Вычислить его площадь.
Найти сторону квадрата, равновеликого равнобедренному треугольнику, боковая сторона которого = 12 ½ лин. един., а высота относится к основанию, как 2 : 3.
Стороны параллелограмма равны a и b и один из его углов = 45°. Найти формулу для его площади.
Угол параллелограмма = 30°; выразить его площадь чрез его стороны (a и b).

232. В п. 229 мы нашли зависимость между сторонами прямоугольного треугольника. Можно найти подобную же зависимость для сторон (с присоединением еще одного отрезка) косоугольного треугольника.

Пусть имеем сначала ∆ABC (чер. 228) такой, чтобы ∠A был острый. Постараемся найти выражение для квадрата стороны BC, лежащей против этого острого угла (подобно тому, как в п. 229 нашли выражение для квадрата гипотенузы).

Построив BD ⊥ AC, получим из прямоугольного треугольника BDC:

BC 2 = BD 2 + DC 2

Заменим BD2, определяя его из ABD, откуда имеем:

BD 2 = AB 2 – AD 2 ,

а отрезок DC заменим чрез AC – AD (очевидно, что DC = AC – AD). Тогда получим:

BC 2 = AB 2 – AD 2 + (AC – AD) 2 = AB 2 – AD 2 + AC 2 – 2AC · AD + AD 2

Выполнив приведение подобных членов, найдем:

BC 2 = AB 2 + AC 2 – 2AC · AD.

Эта формула читается: квадрат стороны треугольника, лежащей против острого угла, равен сумме квадратов двух его других сторон, минус удвоенное произведение одной из этих сторон на ее отрезок от вершины острого угла до высоты .

233. Пусть теперь ∠A и ∆ABC (чер. 229) тупой. Найдем выражение для квадрата стороны BC, лежащей против тупого угла.

Построив высоту BD — она теперь расположится несколько иначе: на 228 где ∠A острый, точки D и C располагаются по одну сторону от A, а здесь, где ∠A тупой, точки D и C расположатся по разные стороны от A. Тогда из прямоугольного ∆BDC получим:

BC 2 = BD 2 + DC 2

Мы можем BD2 заменить, определяя его из прямоугольного ∆BDA:

BD 2 = AB 2 – AD 2 ,

а отрезок DC = AC + AD, что очевидно. Заменяя, получим:

BC 2 = AB 2 – AD 2 + (AC + AD) 2 = AB 2 – AD 2 + AC 2 + 2AC · AD + AD 2

Выполняя приведение подобных членов найдем:

BC 2 = AB 2 + AC 2 + 2AC · AD,

т. е. квадрат стороны треугольника, лежащей против тупого угла, равен сумме квадратов двух его других сторон, плюс удвоенное произведение одной из них на ее отрезок от вершины тупого угла до высоты .
Эта формула, а равно и формула п. 232, допускают геометрическое истолкование, которое легко найти.

234. Пользуясь свойствами пп. 229, 232, 233, мы можем, если нам даны стороны треугольника в числах, узнать, есть ли у этого треугольника прямой или тупой угол.

Прямой или тупой угол в треугольнике может быть расположен лишь против большей стороны, каков же угол против нее, легко узнать: этот угол острый, прямой или тупой, смотря по тому, будет ли квадрат большей стороны меньше, равен или больше суммы квадратов двух других сторон.

Узнать, имеется ли прямой или тупой угол в следующих треугольниках, определяемых своими сторонами:

1) 15 дм., 13 дм. и 14 дм.; 2) 20, 29 и 21; 3) 11, 8 и 13; 4) 7, 11 и 15.

235. Пусть имеем параллелограмм ABCD (чер. 230); построим его диагонали AC и BD и его высоты BK ⊥ AD и CL ⊥ AD.

Тогда, если ∠A (∠BAD) острый, то ∠D (∠ADC) непременно тупой (ибо их сумма = 2d). Из ∆ABD, где ∠A считаем острым, имеем:

BD 2 = AB 2 + AD 2 – 2AD · AK,

а из ∆ACD, где ∠D тупой, имеем:

AC 2 = AD 2 + CD 2 + 2AD · DL.

Заменим в последней формуле отрезок AD равным ему отрезком BC и DL равным ему AK (DL = AK, ибо ∆ABK = ∆DCL, в чем легко убедиться). Тогда получим:

AC2 = BC2 + CD2 + 2AD · AK.

Сложив выражение для BD2 с последним выражением для AC 2 , найдем:

BD 2 + AC 2 = AB 2 + AD 2 + BC 2 + CD 2 ,

так как члены –2AD · AK и +2AD · AK взаимно уничтожаются. Полученное равенство можем прочитать:

Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.

236. Вычисление медианы и биссектора треугольника по его сторонам . Пусть в треугольнике ABC (чер. 231) построена медиана BM (т. е. AM = MC). Зная стороны ∆ABC: BC = a, AC = b и AB = c, вычислить медиану BM.

Продолжим BM и отложим отрезок MD = BM. Соединив D с A и D с C, получим параллелограмм ABCD (выяснить это легко, так как ∆AMD = ∆BMC и ∆AMB = ∆DMC).

Называя медиану BM чрез m, получим BD = 2m и тогда, пользуясь предыдущим п., имеем:

237. Вычисление радиуса, описанного около треугольника круга. Пусть около ∆ABC (чер. 233) описан круг O. Построим диаметр круга BD, хорду AD и высоту треугольника BH.

∆BCH (∠A = ∠H = d — угол A прямой, потому что он вписанный, опирающийся на диаметр BD и ∠D = ∠C, как вписанные, опирающиеся на одну дугу AB). Поэтому имеем:

или, называя радиус OB чрез R, высоту BH чрез h и стороны AB и BC, как и раньше, соответственно чрез c и a:

но площадь ∆ABC = Q = bh/2, откуда h = 2Q/b.

Следовательно, R = (abc) / (4Q).

Мы умеем (п. 230 зад. 3) вычислять площадь треугольника Q по его сторонам. Отсюда можем вычислить R по трем сторонам треугольника.

238. Вычисление радиуса вписанного в треугольник круга. Впишем в ∆ABC, стороны которого даны (чер. 234), круг O. Соединив его центр O с вершинами треугольника и с точками касания D, E и F сторон к кругу, найдем, что радиусы круга OD, OE и OF служат высотами треугольников BOC, COA и AOB.

Читайте также: