Как представлены дробные числа в памяти компьютера

Обновлено: 06.07.2024

Высказывания и их логические связки

Многие математические понятия удобно записывать в виде выражений, содержащих некоторые логические символы. Так, символ , называеый квантором общности, используется вместо слов: «для любого», «для всех», «каково бы ни было…» и т.д., а символ – квантор существования – вместо слов «существует», «найдется хотя бы один …», «имеется» и т.д.

Основной объект математической логики - высказывание. Высказыванием называется повествовательное предложение, которое может быть классифицировано либо как истинное, либо как ложное, но не как и то и другое вместе.

Содержание высказывания несущественно: лишь бы это предложение могло быть либо истинным, либо ложным. При этом вовсе не обязательно указывать способ проверки истинности. Главное, что высказывание не может быть истинным и ложным одновременно. Если высказывание истинно, будем говорить, что его значение истинности - истина (или (от английского true); если ложно, то значение истинности – ложь ( от false).

Высказывания в математической логике обычно обозначаются прописными латинскими буквами: , , и т.д. Для того чтобы из высказываний получать новые высказывания, применяются специальные операции - логические связка. Рассмотрим пять основных логических связок. Сначала дадим неформальное объяснение. Однако оно чревато неточностями, поэтому дадим логическим операциям также строгое определение. Определить высказывание — значит указать, в каких случаях оно истинно, а в каких ложно.

Отрицание — это высказывание, которое получается из данного высказывания с помощью слова «не». Отрицание можно обозначать по-разному: , , .

Простое добавление слова «не» к высказыванию чаще всего будет противоречить языковым нормам. Поэтому в конкретных случаях требуется «перевод» полученного высказывания на русский язык. Пусть, например, = «Завтра пойдет дождь». Что значит «Не (Завтра пойдет дождь)»: «Дождь пойдет не завтра», «Завтра пойдет не дождь» или «Завтра не пойдет дождь»? Здравый смысл подсказывает, что отрицанием высказывания является третье предложение. Чтобы определить точно, дадим формальное определение отрицания.

Отрицанием высказывания называется такое высказывание, которое принимает значение (ложно), если высказывание истинно, и значение (истинно), если высказывание ложно. В нашем примере этому условию удовлетворяет только третье предложение. Итак, = «Завтра не пойдет дождь».

Дизъюнкция - это высказывание, которое получается из двухданных высказываний и с помощью союза «или». Дизъюнкция обозначается .
Дизъюнкция строится с помощью неисключающего «или». Таким
образом, дизъюнкция истинна, когда истинно по крайней мере
одно из высказываний и или оба вместе. Другими словами,дизъюнкция
ложна в том и только в том случае, когда оба высказывания ложны.

Конъюнкция - это высказывание, которое получается из двух данных высказываний и спомощью союза «и». Конъюнкция обозначается . Конъюнкция справедлива в том и только в том случае, когда оба высказывания истинны.

Импликацияобразуется из высказываний и с помощью слов «если. то. ». Получается высказывание вида «если то ». Напомним, что. математическая. логика. носит формальный характер, содержанием высказываний она не, занимается.

На примере импликации хорошо видна разница между обычным языком и языком логики. В обычном языке сложное предложение «если , то » предполагает между и отношение посылки и следствия или же причины и обусловленного ею действия. В логике импликация связывает любые два высказывания.

Импликация обозначается , при этом говорят: « влечет » или « при условии, что », « , если », « есть достаточное условие для », « есть необходимое условие для ».

Договорились, что импликация ложна в том и только в том случае, когда высказывание истинно, а высказывание ложно. Такое определение подсказано здравым смыслом: разумно считать импликацию истинной, если истинно, независимо от значения ; если оба участника импликации ложны, импликация, естественно, также истинна. В единственном случае, когда «предпосылка» импликации истинна, а «вывод» ложен, импликация считается ложной.

Эквиваленция образуется из высказываний и с помощью слов «. тогда и только тогда, когда. »:

Утверждение « тогда и только тогда, когда » не означает в логике, что составляющие высказывания и имеют одно и то же значение или один и тот же смысл.

Эквиваленция обозначается . Синонимы для эквиваленции: «если , то , и если , то », « в том и только в том случае, когда », «И есть необходимое и достаточное условие для », « есть необходимое и достаточное условие для ». Разумное определение эквиваленции: эквиваленция истинна в том и только в том случае, когда высказывания и имеют одинаковое значение истинности (либо оба истинны, либо оба ложны).

Новые высказывания (отрицание, дизъюнкция, конъюнкция, импликация и эквиваленция) образуются из существующих высказываний с помощью операций, или логических связок, имеющих те же названия.

В логике, как и в арифметике, операции делятся по старшинству. Это позволяет при записи сложных высказываний избегать большого количества скобок. Порядок выполнения операций таков: приоритет имеет отрицание, затем на одном уровне — дизъюнкция и конъюнкция, следующая связка — импликация и, наконец, самая последняя — эквиваленция.

Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.

Информатика. 10 класса. Босова Л.Л. Оглавление

§13. Представление чисел в компьютере

Самым первым видом данных, с которыми начали работать компьютеры, были числа. ЭВМ первого поколения могли производить только математические расчёты (вычисления).

Из курса информатики основной школы вы помните, что компьютеры работают с целыми и вещественными числами. Их представление в памяти осуществляется разными способами.

13.1. Представление целых чисел

Во многих задачах, решаемых на компьютере, обрабатываются целочисленные данные. Прежде всего, это задачи экономического характера, при решении которых данными служат количества акций, сотрудников, деталей, транспортных средств и др. Целые числа используются для обозначения даты и времени, для нумерации различных объектов: элементов массивов, записей в базах данных, машинных адресов и т. д. По своей природе множество целых чисел дискретно, т. к. состоит из отдельных элементов.

И хотя любое целое число можно рассматривать как вещественное, но с нулевой дробной частью, предусмотрены специальные способы представления целых чисел. Это обеспечивает: эффективное расходование памяти, повышение быстродействия, повышение точности вычислений за счёт введения операции деления нацело с остатком.

Для компьютерного представления целых чисел используется несколько различных способов, отличающихся друг от друга количеством разрядов (под целые числа обычно отводится 8, 16, 32 или 64 разряда) и наличием или отсутствием знакового разряда.

Беззнаковое представление можно использовать только для неотрицательных целых чисел.

Для получения компьютерного представления беззнакового целого числа в n-разрядной ячейке памяти достаточно перевести его в двоичную систему счисления и, при необходимости, дополнить полученный результат слева нулями до n-разрядов.

Например, десятичные числа 130 и 39 в восьмиразрядном представлении будут иметь вид:

Понятно, что существуют ограничения на числа, которые могут быть записаны в n-разрядную ячейку памяти. Максимальное значение целого неотрицательного числа достигается в случае, когда во всех разрядах ячейки хранятся единицы. Для n-разрядного представления оно будет равно 2 n -1. Минимальное число соответствует n нулям, хранящимся в n разрядах памяти, и равно нулю. Далее приведены диапазоны значений для беззнаковых целых n-разрядных чисел:

При знаковом представлении целых чисел старший разряд ячейки отводится под знак (0 — для положительных, 1 — для отрицательных чисел), а остальные разряды — под цифры числа.

Представление числа в привычной для человека форме «знак-величина», при которой старший разряд ячейки отводится под знак, а остальные разряды — под цифры числа, называется прямым кодом.

Например, прямые коды чисел 48 и -52 для восьмиразрядной ячейки равны:

В математике множество целых чисел бесконечно.

Компьютер работает с ограниченным множеством целых чисел.

Прямой код положительного числа отличается от прямого кода равного по абсолютной величине отрицательного числа только содержимым знакового разряда.

В прямом коде числа можно хранить, но выполнение арифметических операций над числами в прямом коде затруднено — оно требует более сложной архитектуры центрального процессора, «умеющего» выполнять не только сложение, но и вычитание, а также «знающего» особый алгоритм обработки не имеющего «веса» знакового разряда. Этих трудностей позволяет избежать использование дополнительного кода.

Чтобы понять сущность дополнительного кода, рассмотрим работу реверсивного счётчика, последовательность показаний которого можно представить в виде замкнутого кольца из чисел (рис. 3.5).

Рис. 3.5. Реверсивный счётчик

При возрастании показаний счётчика до максимального, например до 999, следующими его состояниями должны быть 1000, 1001, 1002 и т. д. Но для изображения старшей единицы в счётчике не хватает разряда, происходит переполнение разрядной сетки. Поэтому мы увидим 000, 001, 002 и т. д.

При убывании показаний счётчика после состояния 000 будут идти 999, 998, 997 и т. д. Но после достижения нуля последовательное вычитание единицы должно давать -1, -2, -3 и т. д.

Будем рассматривать числа 999, 998, 997 как коды чисел -1, -2, -3 и проверим на их примере соотношение: у + (-у) = 0:

1 + 999 = 1000;
2 + 998 = 1000;
3 + 997 = 1000.

С учётом того что единица переполнения теряется, мы, сложив число и код противоположного ему числа, получаем ноль!

Вот ещё несколько примеров:

5-2 = 5 + [-2] = 5 + 998 = 1003;
7-5 = 7 + [-5] = 7 + 995 = 1002.

Для устранения неоднозначности в кольце будем считать половину состояний (0-499) кодами нуля и положительных чисел, а оставшуюся половину (500-999) — кодами отрицательных чисел.

Таким образом, дополнительный код положительного числа совпадает с этим числом, а для отрицательного числа он равен дополнению его величины до числа q n , возникающего при переполнении разрядной сетки. Здесь q — основание системы счисления, n — число разрядов в разрядной сетке.

Рассмотрим алгоритм получения дополнительного n-разрядного кода отрицательного числа:

1) модуль числа представить прямым кодом в n двоичных разрядах;
2) значения всех разрядов инвертировать (все нули заменить единицами, а единицы — нулями);
3) к полученному представлению, рассматриваемому как n-разрядное неотрицательное двоичное число, прибавить единицу.

Пример 1. Найдём 16-разрядный дополнительный код отрицательного числа -2017₁₀.

Использование дополнительного кода позволяет свести операцию вычитания чисел к операции поразрядного сложения кодов этих чисел.

Выполним эту операцию в 16-разрядных машинных кодах.

Нам потребуются прямой код числа 48 и дополнительный код числа -2017.

Рассмотрим полученный результат. Это отрицательное число (об этом говорит 1 в знаковом разряде), представленное в дополнительном коде. Перейдём к прямому коду модуля соответствующего числа, по которому сможем восстановить десятичное представление результата.

Прямой код можно получить из дополнительного кода, если применить к нему операцию инвертирования и прибавить единицу.

Получаем: -11110110001₂ = -1969.

13.2. Представление вещественных чисел

В математике множество вещественных чисел непрерывно, бесконечно и не ограничено.

Попробуйте обосновать это утверждение.

Вещественные числа записываются в естественной или в экспоненциальной форме.

В жизни мы чаще пользуемся естественной формой записи чисел, при которой: число представляется последовательностью десятичных цифр со знаком плюс или минус, знак плюс может опускаться, для разделения целой и дробной частей числа используется запятая.

Например: 12,34; 0,0056; -708,9.

В экспоненциальной форме вещественное число а представляется как а = ± m • q p , где m — мантисса числа, q — основание системы счисления, р — порядок числа.

Например, длину некоторого отрезка, равного 47,8 см, можно записать так:

1) 478 • 10 -1 см;
2) 47,8 • 10 0 см;
3) 4,78 • 10 1 см;
4) 0,478 • 10 2 см;
5) 0,000478 • 10 5 см.

Такое многообразие вариантов записи в экспоненциальной форме одного и того же числа не всегда удобно. Для однозначного представления вещественных чисел в компьютере используется нормализованная форма.

Нормализованная запись отличного от нуля вещественного числа 1) — это запись вида а = ± m • q p , где р — целое число (положительное, отрицательное или ноль), m — дробь, целая часть которой содержит одну значащую (ненулевую) цифру, т. е. 1 ≤ m < q.

1) Стандарт IEEE 754.

Примеры нормализации чисел:

1) 31,415926 = 3,1415926 • 10 1 ;
2) 1000 = 1,0 • 10 3 ;
3) 0,123456789 = 1,23456789 • 10 -1 ;
4) 0,0000107₈ = 1,07₈ • 10₈ -5 ;
5) 1000,0001₂ = 1,0000001₂ • 10₂ 11 ;
6) AB,CDEF₁₆ = A,BCDEF₁₆ • 10₁₆ 1 .

Диапазон вещественных чисел в памяти компьютера очень широк, но, тем не менее, ограничен. Множество вещественных чисел, которые могут быть представлены в компьютере, конечно.

Поясним это на примере калькулятора, который производит вычисления в десятичной системе счисления. Пусть это будет калькулятор с десятью знакоместами на дисплее:

• 6 знакомест отводится под мантиссу (одно знакоместо отводится под знак мантиссы, четыре — под цифры мантиссы, одно — под точку, разделяющую целую и дробную части мантиссы);
• одно знакоместо отводится под символ «Е»;
• три знакоместа отводятся под порядок (одно — под знак порядка, два — под цифры порядка).

У калькуляторов первая значащая цифра, с которой и начинается мантисса, изображается перед точкой.

Число 12,34 в таком калькуляторе будет представлено как +1.234Е+01.

Число 12,35 будет представлено как + 1.235Е+01.

Как известно, между числами 12,34 и 12,35 находится бесконечное множество вещественных чисел, например: 12,341; 12,3412; 12,34123 и т. д.

Каждое из этих чисел в нашем калькуляторе будет представлено как + 1.234Е+01. Для последних разрядов у нас просто не хватает знакомест! Аналогичная ситуация имеет место и в компьютерном представлении вещественных чисел, независимо от того, ячейки какой разрядности там использованы.

Получается, что точно мы можем представить в компьютере лишь некоторую конечную часть множества вещественных чисел, а остальные числа — лишь приближённо.

Таким образом, множество вещественных чисел, представляемых в компьютере, дискретно, конечно и ограничено.

САМОЕ ГЛАВНОЕ

В математике множество целых чисел дискретно, бесконечно и не ограничено.

Для компьютерного представления целых чисел используется несколько различных способов, отличающихся друг от друга количеством разрядов (8, 16, 32 или 64 разряда) и наличием или отсутствием знакового разряда. В любом случае компьютерное представление целых чисел дискретно, конечно и ограничено.

В математике множество вещественных чисел непрерывно, бесконечно и не ограничено.

Для компьютерного представления вещественных чисел используется нормализованная запись вещественного числа а = ± m • q p , где q — основание системы счисления, р — целое число (положительное, отрицательное или ноль), m — дробь, целая часть которой содержит одну значащую (ненулевую) цифру, т. е. 1 ≤ m < q.

Компьютерное представление вещественных чисел дискретно, конечно и ограничено.

Вопросы и задания

*7. Найдите десятичные эквиваленты чисел, представленных в дополнительном коде: 1) 00000100; 2) 11111001.

8. Для хранения целого числа со знаком в компьютере используется два байта. Сколько единиц содержит внутреннее представление числа -101, записанного:

1) в прямом коде;
2) в дополнительном коде?

9. Вычислите с помощью калькулятора (приложение Windows) в режиме «Программист» следующие примеры:

Как вы можете объяснить полученные результаты?

10. Запишите десятичные числа в нормализованной форме:

1) 217,934; 2) 75321; 3) 10,0101; 4) 200450.

11. Сравните следующие числа:

1) 318,4785 • 10 9 и 3,184785 • 10 11 ;
2) 218,4785 • 10 -3 и 1847,85 • 10 -4 .

12. Выполните операцию сложения:

1) 0,397621 • 10 3 + 0,2379 • 10 1 ;
2) 0,251452 • 10 -3 + 0,125111 • 10 -2 .

13. Чем ограничивается диапазон представимых в памяти компьютера вещественных чисел?

14. Почему множество вещественных чисел, представимых в памяти компьютера, дискретно, конечно и ограничено?

*15. Попытайтесь самостоятельно сформулировать основные принципы представления данных в компьютере.

Представление дробных чисел в двоичной системе счисления

Дробные числа можно записывать не только в виде десятичных дробей, но и в системах счисления с произвольным основанием. Например, при записи дробных чисел в двоичной системе счисления первая цифра после точки (запятой) соответствует значению \(2^\), вторая цифра — значению \(2^\) и т. д. То есть если число в двоичной системе счисления записывается как \(\overlinea_. a_.a_a_. a_>\), то есть имеет \(n\) цифр до точки и \(m\) цифр после точки, то значение такого числа равно \(a_\cdot 2^+a_\cdot 2^+. +a_\cdot 2^+a_\cdot 2^+a_\cdot 2^+. a_\cdot 2^\).

Например, запись \(0.1011_2\) в двоичной системе счисления является представлением числа \(2^+2^+2^\), то есть равно \(\frac\). При этом в виде конечных дробей в двоичной системе счисления можно записать только такие рациональные числа \(\frac\), где знаменатель \(m\) является степенью двойки, другие же рациональные числа представляются в виде бесконечных двоичных дробей.

Например, \(\frac=2^+2^+2^+. =0.010101. _=0.(01)_\), \(\frac=2^+2^+2^+2^+2^+2^+. =0.0001100110011. _2=0.0(0011)_2\). Из-за этого многие рациональные числа (в том числе число \(\frac\)) не могут быть точно представлены в памяти компьютера, поскольку для их точного представления в двоичной системе счисления требуется бесконечной число знаков, так же как и число \(\frac\) не может быть записана в виде десятичной конечной дроби.

Типы данных для представления действительных чисел

Действительные числа в памяти компьютера хранятся в представлении с плавающей точкой: число хранится в виде мантиссы \(b\) и показателя степени \(p\), в этом случае считается, что число равно \(\cdot 2^p\). Аналогичное представление используется при вводе-выводе чисел, при записи действительных чисел в коде программы. Например, значение постоянной Авогадро, равное \(6.02\cdot10^\) в коде программы или при вводе-выводе следует записать как 6.02e23 , где 6.02 — мантиса, 23 — показатель степени, буква «e» при записи действительных чисел в компьютерных программах используется для разделения записи мантисы и показателя.

Но при представлении действительных чисел используется двоичная система счисления, в которой, например, число \(\frac\) в представлении с плавающей точкой можно записать как \(0.010101. \cdot 2^\), или \(0.0010101. \cdot 2^\), или \(0.10101. \cdot 2^\) или еще бесконечно большим числом способов. Желательно выбрать из всех таких представлений одно (каноническое), которое будет называться нормализованным, в этом представлении целая часть числа всегда равна 1 (за исключением числа 0). Для числа \(\frac\) нормализованным представлением будет представление \(1.0101. \cdot 2^\). Поскольку целая часть у нормализованного представления числа всегда (кроме числа 0) равна 1, то целая часть не хранится, а хранится только дробная часть мантиссы. Количество значащих знаков мантисcы, которое хранится, может быть различным для различных способов представления действительных чисел. Например, в типе данных двойной точности, который в языке Python соответствует типу float, в языке C — типу double, в языке Pascal — типу double, хранится 52 бита дробной части мантисы.

Стандарт IEEE754 определяет несколько типов представления действительных чисел, основными из которых являются числа одинарной точности (для их хранения требуется 4 байта), двойной точности (8 байт) и расширенной точности (10 байт).

Любому, кто хоть раз задумывался в жизни о том, чтобы стать "айтишником" или системным администратором, да и просто связать судьбу с вычислительной техникой, знание о том, как происходит представление чисел в памяти компьютера, абсолютно необходимо. Ведь именно на этом основываются языки программирования низкого уровня, такие как Assembler. Поэтому сегодня мы рассмотрим представление чисел в компьютере и их размещение в ячейках памяти.

Система счисления

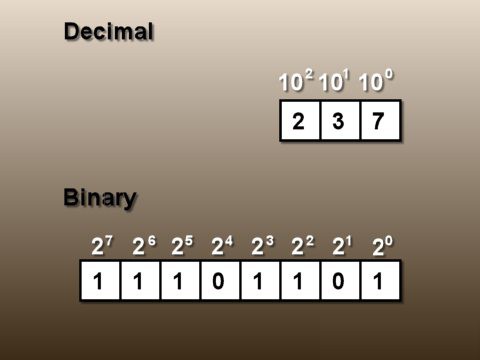
Если вы читаете данную статью, то, скорее всего, уже знаете об этом, но повторить стоит. Все данные в персональном компьютере хранятся в двоичной системе счисления. Это означает, что любое число необходимо представить в соответствующей форме, то есть состоящим из нулей и единиц.

Чтобы перевести привычные для нас десятичные числа к виду, понятному компьютеру, нужно воспользоваться описанным ниже алгоритмом. Существуют и специализированные калькуляторы.

Итак, для того чтобы перевести число в двоичную систему счисления, нужно взять выбранное нами значение и поделить его на 2. После этого мы получим результат и остаток (0 или 1). Результат опять делим 2 и запоминаем остаток. Данную процедуру нужно повторять до тех пор, пока в итоге также не окажется 0 или 1. Затем записываем конечное значение и остатки в обратном порядке, как мы их получали.

Именно так и происходит представление чисел в компьютере. Любое число записывается в двоичной форме, а потом занимает ячейку памяти.

Память

Как вам должно быть уже известно, минимальная единица измерения информации составляет 1 бит. Как мы уже выяснили, представление чисел в компьютере происходит в двоичном формате. Таким образом, каждый бит памяти будет занят одним значением – 1 или 0.

Для хранения больших чисел используются ячейки. Каждая такая единица содержит до 8 бит информации. Поэтому можно сделать вывод, что минимальное значение в каждом отрезке памяти может составлять 1 байт или быть восьмизначным двоичным числом.

Целые

Наконец мы подобрались к непосредственному размещению данных в компьютере. Как было уже сказано, первым делом процессор переводит информацию в двоичный формат, а только затем размещает в памяти.

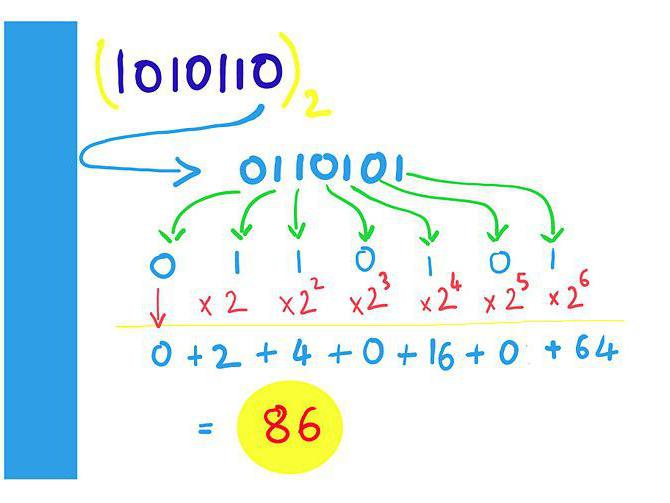
Начнем мы с самого простого варианта, коим является представление целых чисел в компьютере. Память ПК отводит под этот процесс до смешного малое количество ячеек – всего одну. Таким образом, максимум в одном слоте могут быть значения от 0 до 11111111. Давайте переведём максимальное число в привычную нам форму записи.
Х = 1 × 2 7 + 1 × 2 6 + 1 × 2 5 + 1 × 2 4 + 1 × 2 3 + 1 × 2 2 + 1 × 2 1 + 1 × 2 0 = 1 × 2 8 - 1 = 255.

Теперь мы видим, что в одной ячейке памяти может располагаться значение от 0 до 255. Однако это относится исключительно к целым неотрицательным числам. Если же компьютеру понадобится записать отрицательное значение, всё пройдет немного по-другому.

Отрицательные числа

Теперь давайте посмотрим, как происходит представление чисел в компьютере, если они являются отрицательными. Для размещения значения, которое меньше нуля, отводится две ячейки памяти, или 16 бит информации. При этом 15 уходят под само число, а первый (крайний левый) бит отдается под соответствующий знак.

Если цифра отрицательная, то записывается "1", если положительная, то "0". Для простоты запоминания можно провести такую аналогию: если знак есть, то ставим 1, если его нет, то ничего (0).

Оставшиеся 15 бит информации отводятся под число. Аналогично предыдущему случаю, в них можно поместить максимум пятнадцать единиц. Стоит отметить, что запись отрицательных и положительных чисел существенно отличается друг от друга.

Для того чтобы разместить в 2 ячейках памяти значение больше нуля или равное ему, используется так называемый прямой код. Данная операция производится так же, как и было описано, а максимальное А = 32766, если использовать десятичную систему счисления. Сразу хочется отметить, что в данном случае "0" относится к положительным.

Примеры

Представление целых чисел в памяти компьютера не является такой уж трудной задачей. Хотя она немного усложняется, если речь идет об отрицательном значении. Для записи числа, которое меньше нуля, используется дополнительный код.

Чтобы его получить, машина производит ряд вспомогательных операций.

Сначала записывается модуль отрицательного числа в двоичном счислении. То есть компьютер запоминает аналогичное, но положительное значение.
Затем проводится инвертирование каждого бита памяти. Для этого все единицы заменяются нулями и наоборот.
Прибавляем "1" к полученному результату. Это и будет дополнительный код.

Приведем наглядный пример. Пусть у нас есть число Х = - 131. Сначала получаем его модуль |Х|= 131. Затем переводим в двоичную систему и записываем в 16 ячеек. Получим Х = 0000000010000011. После инвертирования Х=1111111101111100. Добавляем к нему "1" и получаем обратный код Х=1111111101111101. Для записи в 16-битную ячейку памяти минимальным числом является Х = - (2 15 ) = - 32767.

Длинные целые

Как видите, представление вещественных чисел в компьютере не так уж и сложно. Однако рассмотренного диапазона может не хватать для большинства операций. Поэтому, для того чтобы разместить большие числа, компьютер выделяет из памяти 4 ячейки, или 32 бита.

Процесс записи абсолютно не отличается от представленного выше. Так что мы просто приведем диапазон чисел, которые могут храниться в данном типе.

Х_мах=2 147 483 647.

Х_min=- 2 147 483 648.

Данных значений в большинстве случаев достаточно для того, чтобы записывать и проводить операции с данными.

Представление вещественных чисел в компьютере имеет свои преимущества и недостатки. С одной стороны, данная методика позволяет проще производить операции между целочисленными значениями, что значительно ускоряет работу процессора. С другой стороны, данного диапазона недостаточно для решения большинства задач экономики, физики, арифметики и других наук. Поэтому теперь мы рассмотрим очередную методику для сверхвеличин.

Плавающая запятая

Это последнее, что вам необходимо знать про представление чисел в компьютере. Поскольку при записи дробей возникает проблема определения положения запятой в них, для размещения подобных цифр в компьютере используется экспоненциальная форма.

Любое число может быть представлено в следующей форме Х = m * р п . Где m – это мантисса числа, р – основание системы счисления и п – порядок числа.

Для стандартизации записи чисел с плавающей запятой используется следующее условие, согласно которому модуль мантиссы должен быть больше или равен 1/п и меньше 1.

Пусть нам дано число 666,66. Приведём его к экспоненциальной форме. Получится Х = 0,66666 * 10 3 . Р = 10 и п = 3.

На хранение значений с плавающей запятой обычно выделяется 4 или 8 байт (32 или 64 бита). В первом случае это называется числом обычной точности, а во втором – двойной точности.

Из 4 байт, выделенных под хранение цифр, 1 (8 разрядов) отдается под данные о порядке и его знаке, а 3 байта (24 разряда) уходят на хранение мантиссы и её знака по тем же принципам, что и для целочисленных значений. Зная это, мы можем провести нехитрые расчеты.

Максимальное значение п = 1111111 2 = 127 10 . Исходя из него, мы можем получить максимальный размер числа, которое может храниться в памяти компьютера. Х=2 127 . Теперь мы можем вычислить максимально возможную мантиссу. Она будет равна 2 23 – 1 ≥ 2 23 = 2 (10 × 2,3) ≥ 1000 2,3 = 10 (3 × 2,3) ≥ 10 7 . В итоге, мы получили приближенное значение.

Если теперь мы объединим оба расчета, то получим значение, которое может быть записано без потерь в 4 байта памяти. Оно будет равно Х = 1,701411 * 10 38 . Остальные цифры были отброшены, поскольку именно такую точность позволяет иметь данный способ записи.

Двойная точность

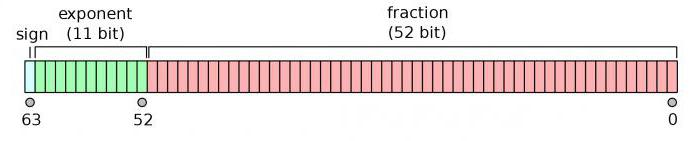
Поскольку все вычисления были расписаны и объяснены в предыдущем пункте, здесь мы расскажем всё очень коротко. Для чисел с двойной точностью обычно выделяется 11 разрядов для порядка и его знака, а также 53 разряда для мантиссы.

П = 1111111111 2 = 1023 10 .

М = 2 52 -1 = 2 (10*5.2) = 1000 5.2 = 10 15.6 . Округляем в большую сторону и получаем максимальное число Х = 2 1023 с точностью до "м".

Надеемся, информация про представление целых и вещественных чисел в компьютере, которую мы предоставили, пригодится вам в обучении и будет хоть немного понятнее, чем то, что обычно пишут в учебниках.

Читайте также: