Матрица полученная из данной заменой каждой ее строки столбцом с тем же номером называется
Обновлено: 03.07.2024
содействовать формированию познавательного интереса, развитию математических умений в процессе обучения.
Структура занятия.
Актуализация знаний студентов.
Изучение нового материала.
Закрепление изученного материала.
Подведение итогов занятия.
Литература :
П. Е. Данко и др. Высшая математика в упражнениях и задачах.- М: Высшая школа,1999.-4.1-304 с.-1,2 ч.
И.И. Валуцэ, Г.Д. Дилигул. Математика для техникумов. М.: Наука, 1989.
Барковский В.В., Барковская Н.В. Математика для экономистов. Высшая математика.-К.: Национальная академия управления, 1999.-399
Дополнительная литература .
В. В. Пак, Ю.Л. Косенко, Высшая математика. Киев, Лебедь, 1996.
Яковлев Г.Н. Алгебра и начала анализа. М.: Наука, 1977, ч. 1,2.
О.Н. Афанасьева, Я.С. Бродский, І.І. Гуткин, А.Л. Павлов. Сборник задач по математике для техникумов. М.: Наука, 1987.-208 с.
Ход занятия
Организационный момент.
Актуализация знаний студентов.
Изучение нового материала.
1. Матрицы. Основные понятия.
1.1 Основные понятия.
Матрицей называется прямоугольная таблица чисел, содержащая m - строк одинаковой длины (или n - столбцов одинаковой длины).
Матрица записывается в виде:
, где i = 1;2;3;… m – номер строки,
j = 1;2;3;… n – номер столбца.
Матрицу А называют матрицей размера и пишут
Числа, составляющие матрицу, называются ее элементами.
Элементы, стоящие на диагонали, идущей из левого верхнего угла в правый нижний угол, образуют главную диагональ . Другая диагональ называется побочной диагональю .
Матрицы равны между собой, если равны все соответствующие элементы этих матриц.
Матрица, у которой число строк равно числу столбцов, называется квадратной матрицей.
Квадратную матрицу размера называют матрицей n -го порядка.
Квадратная матрица, у которой все элементы, кроме главной диагонали, равны нулю, называют диагональной .
Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной матрицей. И обозначается буквой Е .
-это единичная матрица третьего порядка.
Матрица, все элементы которой равны нулю, называется нулевой . Обозначается буквой О и имеет вид:
В матричном исчислении матрицы О и Е играют роль 0 и 1 в арифметике.
Матрица, содержащая один столбец или одну строку, называется вектором.
А = -это вектор-столбец; В = -это вектор-строка.
Матрица размера , состоящая из одного числа, отождествляется с этим числом, т.е. матрица есть число 5.
1.2. Транспонирование матрицы.
Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей транспонированной к данной.
Транспонированная матрица обладает следующим свойством:
1.3. Операции над матрицами.
1.3.1. Сложение матриц.
Операция сложения матриц вводится только для матриц одинаковых размеров.
Суммой двух матриц и называется матрица
, где i = 1;2;3;… m – номер строки,
j = 1;2;3;… n – номер столбца.
Аналогично определяется разность матриц.
1.3.2.Умножение матрицы на число.
Произведением матрицы на число k называется матрица , такая , что
Если , k =2, тогда .
Матрица называется противоположной матрице А
Разность матриц А-В=А+(- B )
1.3.3. Произведение матриц.
Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.
Произведением матрицы на матрицу называется матрица , такая, что , где i =1… m ; k =1… p , т.е. элемент i -й строки и k -го столбца матрицы произведения С равен сумме произведений элементов i -ой строки матрицы А на соответствующие элементы k -го столбца матрицы В.
Если матрицы А и В квадратные одного размера, то произведения АВ и ВА всегда существуют.
Легко показать, что АЕ=ЕА=А, где
А-квадратная матрица, Е-единичная матрица того же размера.
Пример:Найти АВ и ВА, если
Произведение АВ не определено, т.к. число столбцов матрицы А не совпадает с числом строк матрицы В.
Произведение ВА считается так :
Матрицы А и В называются перестановочными, если
Умножение матриц обладает следующими свойствами:
k ( AB )=( kA ) B , если написанные суммы и произведения матриц имеют смысл.
Для операции транспонирования верны свойства:
1.3. Ранг матрицы.Элементарные преобразования матрицы.
Выделим в матрице строк и столбцов, где —число меньшее или равное наименьшему из чисел и .
О пределителем, порожденным матрицей называется о пределитель порядка , составленный из элементов, стоящих на пересечении строк и столбцов.
Например, пусть , . Тогда , —определител и второго порядка, порожденные матрицей.
Пусть . Тогда — определитель третьего порядка, порожденный данной матрицей.
Рангом матрицы называется наибольший из порядков определителей, отличных от нуля, порожденных данной матрицей. Обозначается или .
Ясно, что если равны нулю все определители порядка , порожденные данной матрицей, то ранг матрицы меньше . Действительно, по определению , каждый из определителей -го порядка выражается линейно через определители -го порядка. Значит , все определители - го порядка равны нулю. Аналогично доказывается, что равны нулю все определители-го и более высоких порядков. Отсюда следует, что ранг матрицы меньше .
Теорема. Ранг матрицы не изменится , если:
а) все строки заменить столбцами;
б) поменять местами две строки ( два столбца);
в) умножить каждый элемент строки (столбца) на один и тот же множитель , отличный от нуля;
г) прибавить к элементам одной строки (столбца) соответствующие элементы другой строки (другого столбца), умноженные на один и тот же множитель.
Преобразования а) — г) называются элементарными .
Элементарными преобразованиями матриц являются:
- перестановка местами двух параллельных рядов матрицы;
- умножение всех элементов ряда матрицы на число, отличное от нуля;
- прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда , умноженных на одно и то же число.
Две матрицы А и В называются эквивалентными, если одна из них получается из другой с помощью элементарныхпреобразований.
Записывается так: A
При помощи элементарных преобразований любую матрицу можно привести к матрице, у которой в начале главной диагонали стоят подряд несколько единиц, а все остальные элементы равны нулю.
Такую матрицу называют канонической.
Пример: Привести матрицу к каноническому виду:
Выполним элементарные преобразования:
(переставим местами первый и третий столбцы, затем прибавим ко всем элементам второй строки соответствующие элементы первой строки, а ко всем элементам третьей строки прибавим соответствующие элементы первой строки, умноженные на -5)
(прибавим к элементам второго столбца соответствующие элементы первого столбца, умноженные на -3, а к элементам третьего и четвертого столбца соответствующие элементы первого столбца, умноженные на -2)
(разделим второй, третий и четвертый столбцы на 5; 2 и 3 соответственно)
продолжая элементарные преобразования получим:
Пример 8 . Определит е ранг матрицы : .
Приведём матрицу к ступенчатому виду с помощью элементарных преобразований:

Матрица называется прямоугольн ой , если количество ее строк не совпадает с количеством столбцов :
Матрица называется квадратной , если количество ее строк совпадает с количеством столбцов :
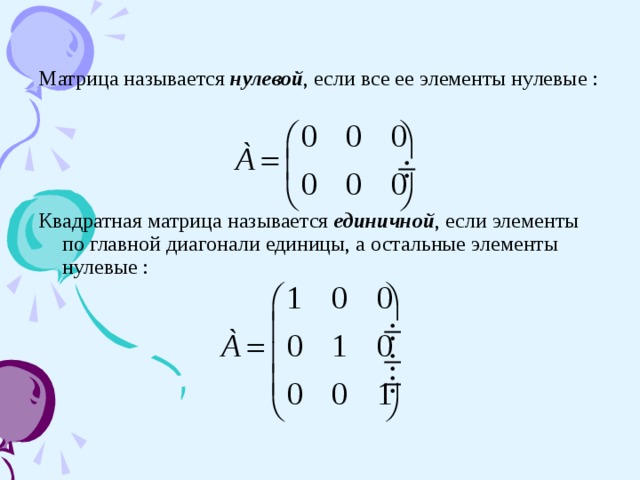
Матрица называется нулевой , если все ее элементы нулевые :
Квадратная матрица называется единичной , если элементы по главной диагонали единицы, а остальные элементы нулевые :

Квадратная матрица называется диагональной , если элементы по главной диагонали отличны от нуля, а остальные элементы нулевые :
Квадратная матрица называется симметричной , если относительно главной диагонали для всех ее элементов выполняется условие :

Квадратная матрица называется вырожденной , если ее определитель равен нулю.
Матрицы А и В (одинаковых размерностей) называются равными , если :

Квадратные матрицы вида
называются треугольными .
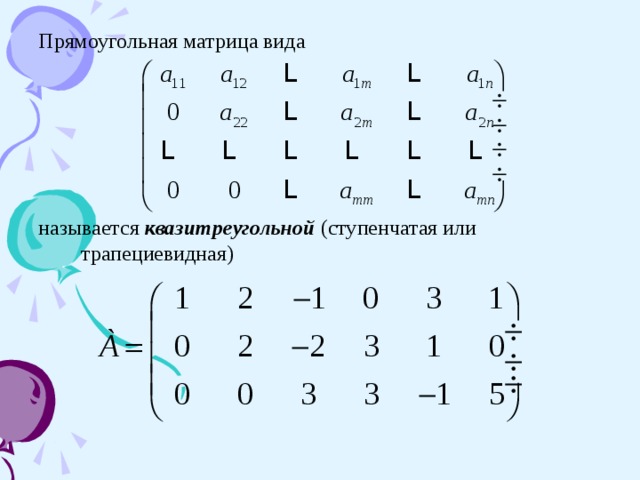
Прямоугольная матрица вида
называется квазитреугольной (ступенчатая или трапециевидная)

Матрица, состоящая из одной строки называется матрицей-строкой или строчной матрицей .
Матрица, состоящая из одного столбца называется матрицей-столбцом или столбцевой матрицей
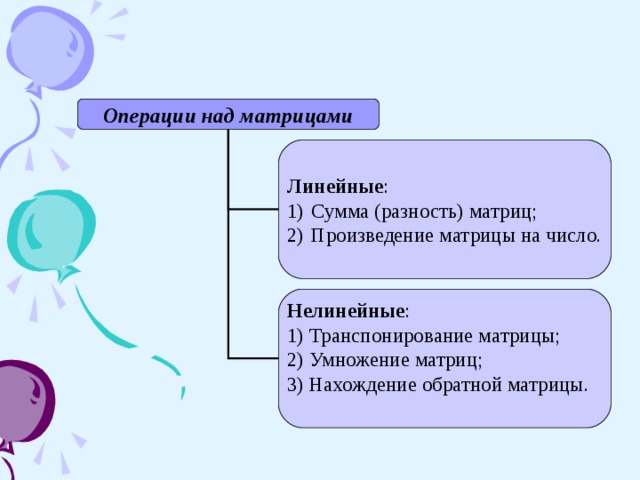
Операции над матрицами
- Сумма (разность) матриц;
- Произведение матрицы на число.
1) Транспонирование матрицы;
2) Умножение матриц;
3) Нахождение обратной матрицы.

Суммой (разностью) двух матриц одинаковой размерности называется матрица, элементы которой равны сумме (разности) соответствующих элементов матриц слагаемых.
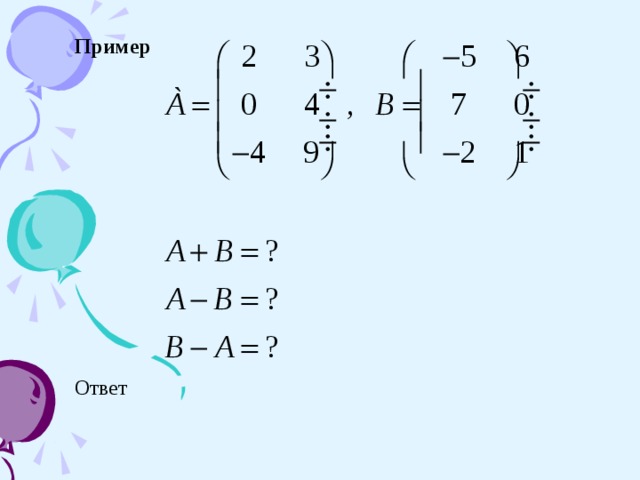

Произведением матрицы на число называется матрица, полученная из данной умножением всех ее элементов на число.

Линейные операции обладают следующими свойствами :
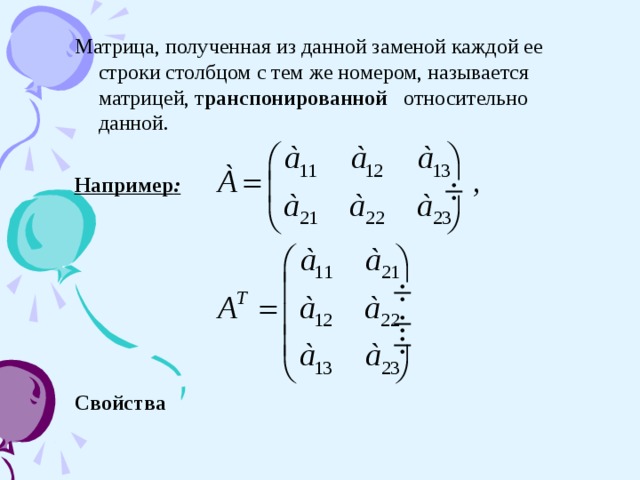
Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей, т ранспонированной относительно данной.

Умножение матриц определяется для согласованных матриц.
Произведением матрицы на матрицу называется матрица , для которой ,
т.е. каждый элемент матрицы С равен сумме произведений элементов i -й строки матрицы А на соответствующие элементы j -го столбца матрицы В.

Читайте также:

